Let Sk,k=1,2,,100, denotes thesum of the infinite geometric series whose first term s k−1k! and the common ratio is 1k , then the value of 1002100!+100∑k=2(k2−3k+1)Sk is _______.
Sk=a1−r=k−1k!1−1k=kk!=1(k−1)!
Now, 100∑k=2∣∣(k2−3k+1)Sk∣∣=100∑k=2∣∣∣(k2−3k+1)⋅1(k−1)!∣∣∣
=100∑k=2∣∣∣(k−1)(k−2)=k(k−1)!∣∣∣
=∣∣∣10!−21!∣∣∣+∣∣∣21!−32!∣∣∣+∣∣∣32!−43!∣∣∣+.........+∣∣∣9998!−10099!∣∣∣
=(21!−10!)+(21!−32!)+(32!−43!)+.........+(9998!−10099!)
=3−10099=3−(100)2100!
∴(100)2100!+100∑k=2∣∣(k2−3k+1)Sk∣∣=3.
Topper's Solved these Questions
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (Subjective Type Questions)
Explore 24 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHSChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
Similar Questions
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
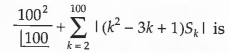 is
is
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View Solution
Knowledge Check
Let Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k.k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
A3B2C1D0Let Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
A1−4loge√2Bloge2−1C1−loge2D1−loge4Let SK be the sum of an infinte G.P. series whose first term is K and common ratio is KK+1(K>0). Then the value of ∞∑K=1(−1)KSK is equal to
Aloge4Bloge2−1Cloge2+1D1−loge4
Let Sk denote sum of infinite geometric series (K=1,2,3,.......), where first term is (k2−1) and common ratio is 1K, then the unit digit of the sum (∞∑k=1Sk2k−1), is
View SolutionFor k=2,3,…, let Sk denote the sum of the infinite G.P. whose first term is k2+k−2 and common ratio is 1k, then ∞Σk=1Sk2k=
View SolutionFind the value of limn→∞n∑k=1k2+k−1(k+1)!.
View SolutionFind the value of 2551 S where S=50∑k=1kk4+k2+1
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View Solution

