If an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an
Video Solution
Text Solution
∴Bn=1−An>An⇒An<12
Now, An=34(1−(−34)n)1+34<12⇒(−34)n>−16
Obviously, it is true for all even values of n.
But for n=1,−34<−16
n=3(−34)3=−2724<−16
n=5,(−34)5=−2431024>−16
which is true for n=7 obviously, n0=7
Aliter Bn=1−An>An
⇒An<12⇒34(1−(−34)n)1+34<12⇒(−34)n>−16
Obviously, it is true for all even values of n.
But for n=1,−34<−16
n=3,(−34)3=−2764<−16
n=5,(−34)5=−2431024<−16
and for n=7⇒(−34)7=−218712288>−16
Hence, minimum natural number n0=7.
|
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Subjective Type Questions)
24 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
Knowledge Check
IF an=1n+1+1 then find the value of a1+a3+a5
A1712B2712C3712D4712If 1.3+2.32+3.33+...=n3n=(2n−1)3+b4, then a and b are respectively:
An,2Bn,3Cn+1,2Dn+1,3
Let An=34−(34)2+(34)3−...+(−1)n−1(34)nandBn=1−An, then find the least value of n0,n0∈N such that Bn>An,∀n≥n0.
View SolutionComplete the following statements.
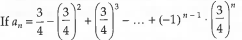 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View Solution13+23+33+.....+n3=n(n+1)24,n∈N
View Solution1+5+9+...+(4n−3)=n(2n−1) for all natural numbers n
View SolutionIn an AP, given an=4,d=2,Sn=−14 find n and a
View Solution∞∑n=1(14n−3−14n−1)=πn find n
View Solution
