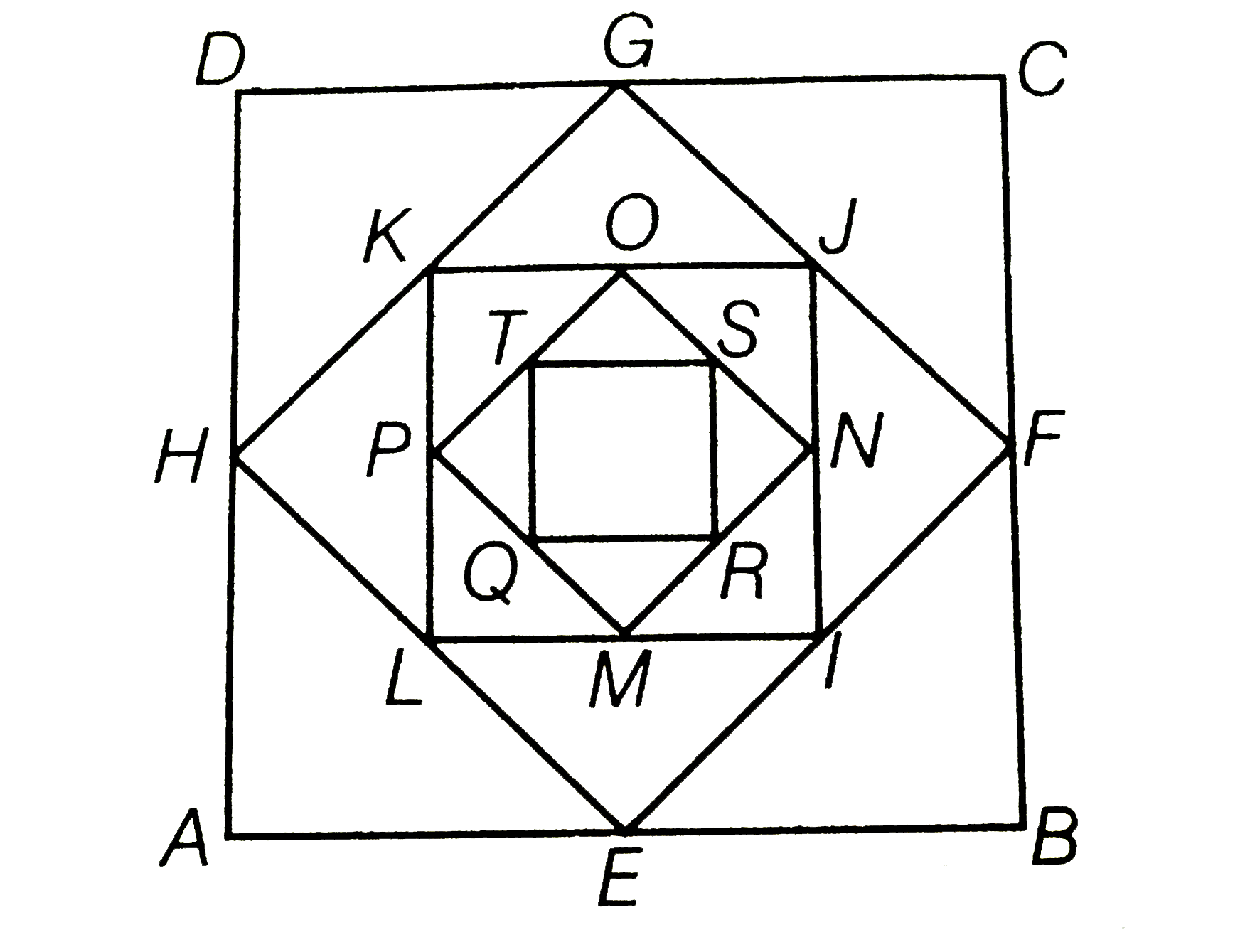
A square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?

Video Solution

Text Solution

Verified by Experts

Let a be the side lengh of square, than
$A B = B C = C D = D A = a$
$∴$ E,F,G,H are the mid-points of AB,BC,CD and DA, respectively.
$∴ E F = F G = G H = H E = \frac{a}{\sqrt{2}}$
and I,J,K,L are the mid-points of EF,FG,GH and HE, respectively.
$∴ I J = J K = K L = L I = \frac{a}{2}$
Similarly, $M N = N O = O P = P M = \frac{a}{2 \sqrt{2}}$ and $Q R = R S = S T = T Q = \frac{a}{4}, .....$
S=Sum of areas = $A B C D + E F G H + I J K L + M N O P + Q R S T + ...$
$a^{2} + {(\frac{a}{\sqrt{2}})}^{2} + {(\frac{a}{\sqrt{2}})}^{2} + {(\frac{a}{2 \sqrt{2}})}^{2} + ....$
$= a^{2} (1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...)$
$= a^{2} ⎛ ⎝ \frac{1}{1 - \frac{1}{2}} ⎞ ⎠ = 2 a^{2} = 2 {(16)}^{2} [∴ a = 16 cm]$
$= 512 s q cm$
.

Updated on:21/07/2023

A square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
(a)256sq. Cm
(b)512 sq. cm
(c)1024sq. Cm
(d)512/3sq. Cm
A256sq. Cm
B512 sq. cm
C1024sq. Cm
D512/3sq. Cm
A square is drawn by joining the mid points of the sides of a given square. A third square is drawn inside the second square in the same way and this process continues indefinitely. If a side of the first square is 4 cm, determine the sum of the areas of all the squares :
A $32 c m^{2}$
B $16 c m^{2}$
C20
Dnone of these
A square is drawn by joining the mid points of the sides of a given square. A third square is drawn inside the second square in the same way and this process continues indefinitely. If a side of the first square is 4 cm, determine the sum of the areas of all the squares :
A $32 c m^{2}$
B $16 c m^{2}$
C20
Dnone