Find the sum of first 24 terms of on AP t1,t2,t3,...., if it is known that t1+t5+t10+t15+t20+t24=225.
Video Solution
Text Solution
We know that, in an AP the sums of the terms equidistant from the beginning and end is always same and is equal to the sum of first and last term.
Then, t1+t24=t5+t20=t10+t15
but given t1+t5+t10+t15+t20+t24=225
⇒(t1+t24)+(t5+t20)+(t10+t15)=225
⇒3(t1+t24)=225
⇒t1+t24=75
∴S24=242(t1+t24)=12×75=900
|
Topper's Solved these Questions
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise For Session 1
Explore 5 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise For Session 2
Explore 11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHSChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
Similar Questions
Knowledge Check
Let s1,s2,s3....andt1,t2,t3.... are two arithmetic sequences such that s1=t1≠0,s2=2t2and10∑i=1si=15∑i=1ti. Then the value of s2−s1t2−t1 is
A8/3B3/2C19/8D2In a harmonic progression t1,t2,t3,……………., it is given that t5=20andt6=50. If Sn denotes the sum of first n terms of this, then the value of n for which Sn is maximum is
A6B7C9D10Suppose a series of n terms given by Sn=t1+t2+t3+. . . .+tn
then Sn−1=t1+t2+t3+. . . .+tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. The sum of n terms of a series is a.2n−b. where a and b are constant then the series isAA.PBG.PCA.G.PDG.P from second term onwards
If the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View Solution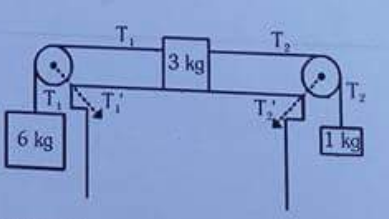
Calculate a, T1,T2,T1'&T2'.
View SolutionIn an A.P., if T1+T5+T10+T15+T20+T24=225, find the sum of its 24 terms.
View SolutionSuppose a series of n terms given by Sn=t1+t2+t3+. . ..+tn
then Sn−1=t1+t2+t3+ . . . +tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. if the sum of n terms of a series a.2n−b then the sum ∞∑r=11tr is
View SolutionIn a H.P., T7=110andT12=125thenT20 is
View Solution

