A sonometer strings $A B$ of length $1 m$ is stretched by a load and the tension $T$ is adjusted so that the string resonates to a frequency of $1 k H z$ . Any point $P$ of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.

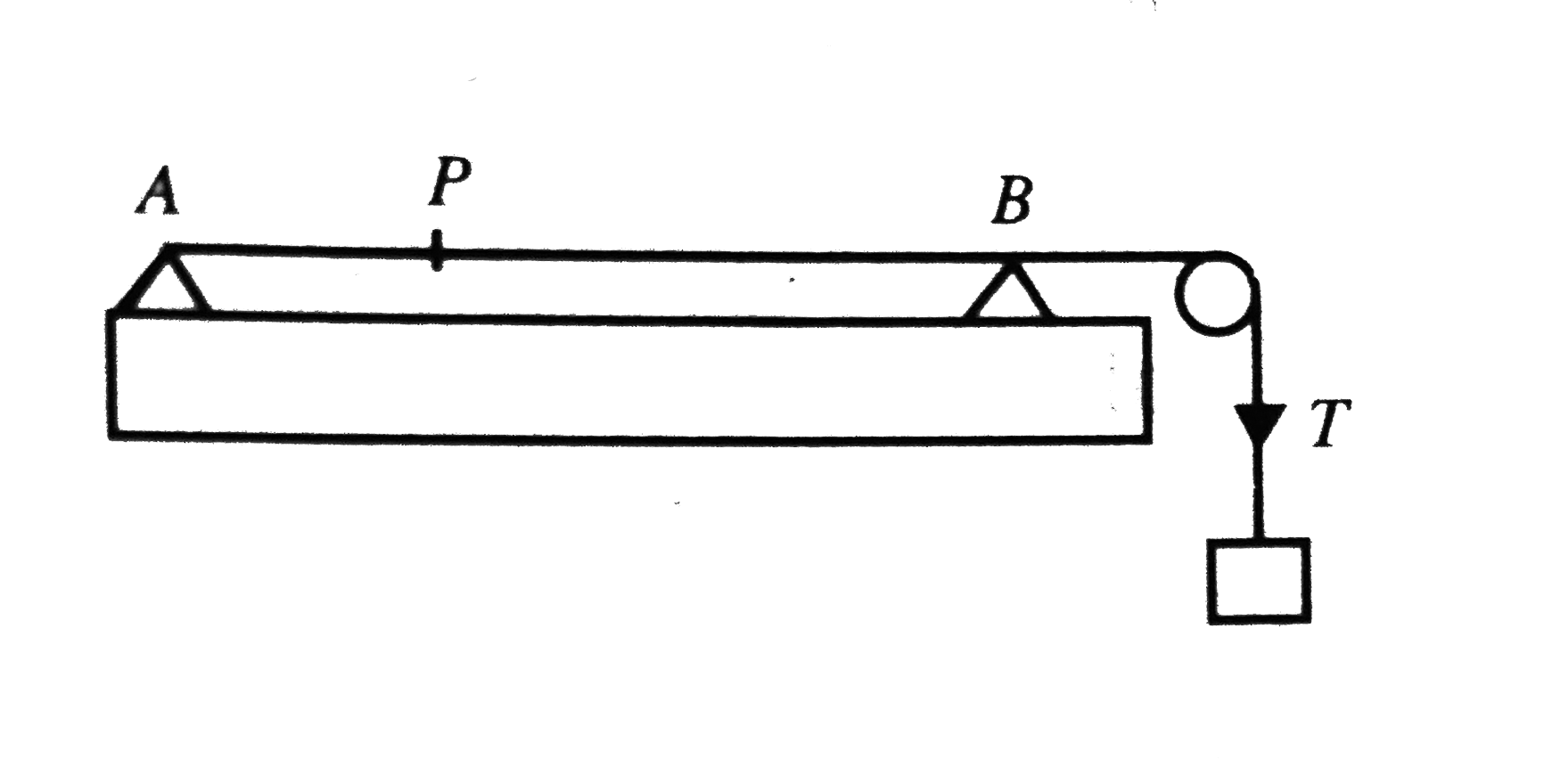
If point $P$ is fixed so that $A P : P B : 1 : 4$ , then the smallest frequency for which the sonometer wire resonates is $5 k H z$ .

If $P$ be taken at midpoint of $A B$ and fixed , then when the wire vibrates in the third harmonic of its fundamental , the number of nodes in the wire ( including $A and B$ ) will be totally seven.

If the fixed point $P$ divides $A B$ in the ratio $1 : 2$ , then the tension needed to make the string vibrate at $1 k H z$ will be $3 T$ . (neglecting the terminal effects)

The fundamental frequency of the sonometer wire when $P$ divides $A B$ in the ratio $a : b$ will be the same as the fundamental frequency when $P$ divides $A B$ in the ratio $b : a$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

If $P$ divides $A B$ in ratio $1 : 4$ , then the fundamental frequency corresponds to $5$ loops , one loop in $A P$ and $4$ loops in $P B$ which corresponds to $5 t h$ harmonic of $1 k H z$ . Hence fundamental $= 5 k H z$ .
If $P$ be taken at midpoint , the third harmonic will have three loops in each half of the wire $A B$ . Hence total number of nodes (including $A$ and $B$ ) will be $5 + 2 = 7$ .
If $P$ divides $A B$ in the ratio $1 : 2$ , the fundamental will have three loops , corresponding to the frequency of $3 k H z$ . For this string to vibrate with the fundamental of $1 k H z$ , the tension must be $(T / 9)$ .
The wire $A B$ will be symmetry , vibrates with the same fundamental frequency when $P$ divides $A B$ in the ratio $a : b$ or in the ratio $b : a$ .

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Knowledge Check

If a sonometer wire of length 110 cm fixed horizontally under a constant tension, then the bridge be placed below the wire so that the two segments can emits note whose frequency are in the ratio 3:2, is
A44cm and 66 cm
B66 cm and 44cm
C25cm and 75cm
D41.5 cm and 58.5 cm
A sonometer wire of length 114 cm is fixed at both the ends. Where should the two bridges be placed so as to divide the wire into three segments whose fundamental frequencies are in the ratio $1 : 3 : 4$ ?
AAt 36 cm and 84 cm from one end
BAt 24 cm and 72 cm from one end
CAt 48 cm and 96 cm from one end
DAt 72 cm and 96 cm from one end
Two stretched strings have lengths 1 and 21 while tensions are T and 4 T respectively. If they are made of same material the ratio of their frequency is
A $2 : 1$
B $1 : 2$
C $1 : 1$
D $1 : 4$

CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Multiple

Home
Ask Doubt
Profile

A sonometer strings AB of length 1m is stretched by a load and the tension T is adjusted so that the string resonates to a frequency of 1kHz. Any point P of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.

The correct Answer is:A, B, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

If a sonometer wire of length 110 cm fixed horizontally under a constant tension, then the bridge be placed below the wire so that the two segments can emits note whose frequency are in the ratio 3:2, is

A sonometer wire of length 114 cm is fixed at both the ends. Where should the two bridges be placed so as to divide the wire into three segments whose fundamental frequencies are in the ratio 1:3:4?

Two stretched strings have lengths 1 and 21 while tensions are T and 4 T respectively. If they are made of same material the ratio of their frequency is

CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Multiple

A sonometer strings $A B$ of length $1 m$ is stretched by a load and the tension $T$ is adjusted so that the string resonates to a frequency of $1 k H z$ . Any point $P$ of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.

A sonometer wire of length 114 cm is fixed at both the ends. Where should the two bridges be placed so as to divide the wire into three segments whose fundamental frequencies are in the ratio $1 : 3 : 4$ ?