A sonometer wire of length 1 m is stretched by a weight of 10 kg. The fundamental frequency of vibration is 100 Hz. Determine the linear density of material of wire.
The correct Answer is:m=0.0025z×10−4 kg/m
To determine the linear density of the sonometer wire, we can follow these steps:
Step 1: Identify the given values
- Length of the wire (L) = 1 m
- Weight (mass) (m) = 10 kg
- Fundamental frequency (f₀) = 100 Hz
- Acceleration due to gravity (g) = 9.8 m/s² (approximately)
Step 2: Calculate the tension (T) in the wire
The tension in the wire is equal to the weight of the mass hanging from it. This can be calculated using the formula:
T=m⋅g
Substituting the values:
T=10kg⋅9.8m/s2=98N
Step 3: Use the formula for fundamental frequency
The formula for the fundamental frequency of a sonometer wire is given by:
f₀=12L√Tμ
Where:
- f₀ = fundamental frequency
- L = length of the wire
- T = tension in the wire
- μ = linear density of the wire
Step 4: Rearrange the formula to solve for linear density (μ)
Rearranging the formula to isolate μ:
f₀=12L√Tμ
Squaring both sides gives:
f₀2=(12L)2Tμ
Rearranging further:
μ=T(2Lf₀)2
Step 5: Substitute the known values into the equation
Now substituting the values we have:
- T=98N
- L=1m
- f₀=100Hz
Calculating:
μ=98(2⋅1⋅100)2
μ=98(200)2
μ=9840000
μ=0.00245kg/m
Or in scientific notation:
μ=2.45×10−3kg/m
Final Answer
The linear density of the material of the wire is 2.45×10−3kg/m.
---
- Length of the wire (L) = 1 m
- Weight (mass) (m) = 10 kg
- Fundamental frequency (f₀) = 100 Hz
- Acceleration due to gravity (g) = 9.8 m/s² (approximately)
The tension in the wire is equal to the weight of the mass hanging from it. This can be calculated using the formula:
T=m⋅g
Substituting the values:
T=10kg⋅9.8m/s2=98N
The formula for the fundamental frequency of a sonometer wire is given by:
f₀=12L√Tμ
Where:
- f₀ = fundamental frequency
- L = length of the wire
- T = tension in the wire
- μ = linear density of the wire
Rearranging the formula to isolate μ:
f₀=12L√Tμ
Squaring both sides gives:
f₀2=(12L)2Tμ
Rearranging further:
μ=T(2Lf₀)2
Now substituting the values we have:
- T=98N
- L=1m
- f₀=100Hz
μ=98(2⋅1⋅100)2
μ=98(200)2
μ=9840000
μ=0.00245kg/m
Or in scientific notation:
μ=2.45×10−3kg/m
The linear density of the material of the wire is 2.45×10−3kg/m.
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Superposition of Waves ( Short Answer II (SA2) ( 3 MARKS Each ) )
6 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Superposition of Waves (Long Answer ( LA) ( 4 marks Each) )
4 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Superposition of Waves (Very Short Answer (VSA) ( 1 MARK Each ) )
13 Videos
- MULTIPLE CHOICE QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MULTIPLE CHOICE QUESTIONSEXERCISE - Communication Systems
6 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
Similar Questions
A wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View SolutionA sonometer wire of length 0.95 m can bear a maximum stress of 9×108N/m2. Calculate the fundamental frequency produced in the wire if density of wire is 8×103kg/m3.
View Solution
Knowledge Check
A sonometer wire of length 0.7 m is stretch by a weight of 4 kg. what is the linear density of the material of the wire, if its fundamental frequency is 200 Hz?
A5×10−3kg/mB5×10−4kg/mC8×10−4kg/mD8×10−3kg/mIn a sonometer wire, the tension is maintained by suspending a 20kg mass from the free end of the wire. The fundamental frequency of vibration is 300Hz.
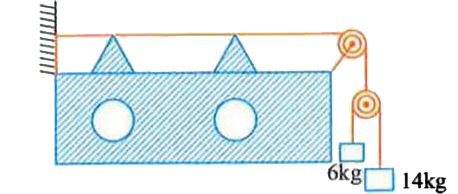
If the tension is provided by two masses of 6kg and 14kg suspended from a pulley as show in the figure the fundamental frequency willAstill remain 300HzBbecome largerCbecome smallerDdecrease in the present situation and increase if the suspended masses of 6kg and 14kg are interchangedIf tension in a sonometer wire is increased by 50% then fundamental frequency of the wire will be increased by 10 Hz. Assuming length as invariable, the frequency of the wire will be
A45.4 HzB55.4 HzC65.4 HzD70 Hz
A 36cm long sonometer wire vibrates with frequency of 280Hz in fundamental mode, when it is under tension of 24.5N. Calculate linear density of the material of wire.
View SolutionThe length of a stretched wire is 1 m and its fundamental frequency is 300 Hz.What is the speed of the transverse wave in the wire ?
View SolutionThe fundamental frequency of vibration of a wire fo certain length is 200 Hz. What will be the fundamental frequency of vibration, if the tension is made double and length of the wire is also doubled ?
View SolutionA stretched sonometer wire of length 1 meter has a fundamental frequency of 50 Hz. If it is plucked at 25 cm, by keeping the bridge at 50 cm, the frequency of vibration of the string would be,
View SolutionA sonometer wire having a length of 50 cm is vibrating in the fundamental mode with a frequency of 100Hz. Which of the following is the type of propagating wave and its speed?
View Solution
