Following are equations of four waves :
(i) y1=asinω(t−xv)
(ii) y2=acosω(t+xv)
(iii) z1=asinω(t−xv)
(iv) z1=acosω(t+xv)
Which of the following statements are correct ?
On superposition of waves (i) and (iii) , a travelling wave having amplitude a√2 will be formed
Superposition of waves (ii) and (iii) is not possible
On superposition of waves (i) and (ii) , a travelling wave having amplitude a√2 will be formed
On superposition of (iii) and (iv) , a transverse stationary wave will be formed
The correct Answer is:A, D
New wave =y1ˆj+z1ˆk
=(aˆj+aˆk)sinω(t−xv)
Amplitude =∣∣aˆj+aˆk∣∣=a√2
(i) and (ii) are travelling in opposite directions , so they will form stationary waves.
Similarly (iii) and (iv) will make the stationary wave.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Assertion - Reasoning
Explore 6 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Comprehension
Explore 55 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Single Correct
Explore 144 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
Knowledge Check
Wave equations of two particles are given by y1=asin(ωt−kx),y2=asin(kx+ωt), then
AThey are moving in opposite directionBPhase between them is 90∘CPhase between them is 180∘DPhase between them is 0∘Two wave are represented by equation y1=asinωt and y2=acosωt the first wave :-
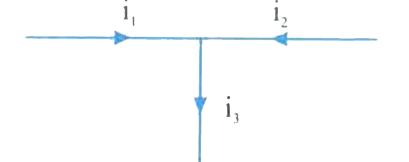
Aleads the second by πBlags the second by πCleads the second by π2Dlags the second by π2If i1=3sinωtand(i2)=4cosωt, then (i3) is
 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
Four different independent waves are represented by
(i) y1=a1sinωt , (ii) y2=a2sin2ωt
(iii) y3=a3cosωt , (iv) y4=a4sin(ωt+π3)
With which two waves interference is possible
View SolutionThe ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
View SolutionFour sound sources produce the following four waves
(i) y1=asin(ωt+ϕ1)
(ii) y2=asin2ωt
(iii) y3=a'sin(ωt+ϕ2)
(iv) y4=a'sin(3ωt+ϕ)
Superposition of which two waves gives rise to interference?
View SolutionThe equations of two SH M's are
X1=4sin(ωt+π/2).X2=3sin(ωt+π)
View SolutionTwo waves are represented by y1=asin(ωt+π6)andy2=acosωt. What will be their resultant amplitude
View Solution