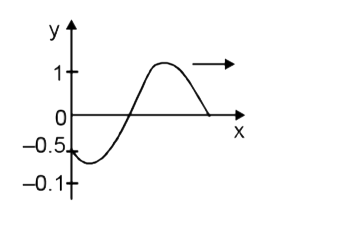
Figure .shows two snapshots of medium particle supporting a plane progressive wave travelling along positive x-axos, corresponding to instants t=0.002s and t=0.008s, respectively shown by curves numbered 1 and 2.
Assume that the interval between the two snapshots is less than the time period.
The frequency of the wave
52s−1
205s−1
104s−1
54s−1
The correct Answer is:c
From the graph it is clear
wave velocity v=(8−3)0.006
v=5×1036m/s
And wave velocity v=fλ
5×1036=f(9−1)⇒f=5×1036×8=104s−1 Let y=Asin(ωt−kx+ϕ)
for curve (1):
−1√2=1sin(ω+ϕ)=−1√2
⇒sin(0.002ω+ϕ)=5π4 or (7pi)/(4)<br>butasthevelocityisdownward<br>so0.002omega+phi=(5pi)/(4)<br>Forcurve(2):<br>1=1 sin (omegaxx0.008+phi)<br>implies0.008omega+phi=2pi+(pi)/(2)FromEqs.(i)and(ii),<br>6omega=1250pi<br>impliesf=(1250pi)/(12pi)=104 Hz<br>v=f lambda=(1250)/(12)xx8=(2500)/(3)m//s
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Assertion-Reasoning
Explore 6 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICSChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
Knowledge Check
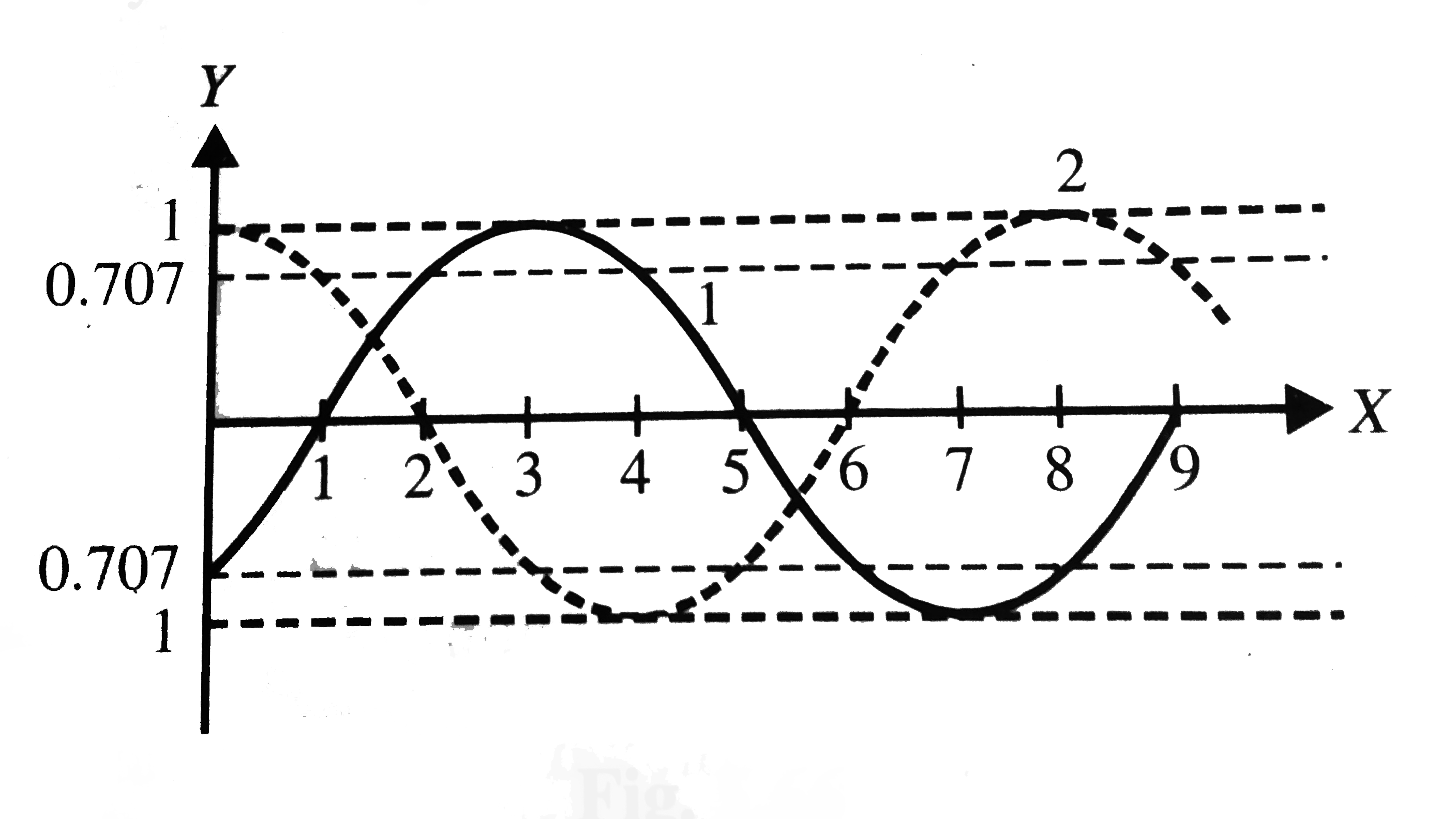
Figure. shows two snapshots of medium particle supporting a plane progressive wave travelling along positive x−axos, corresponding to instants t=0.002s and t=0.008s, respectively shown by curves numbered 1 and 2.
Assume that the interval between the two snapshots is less than the time period.

Velocity of the wave isA17003m/sB17005m/sC25007m/sD25003m/sthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by
 Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)The equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by :-
_E01_059_Q01.png) .Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
.Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
A progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:
View SolutionThe
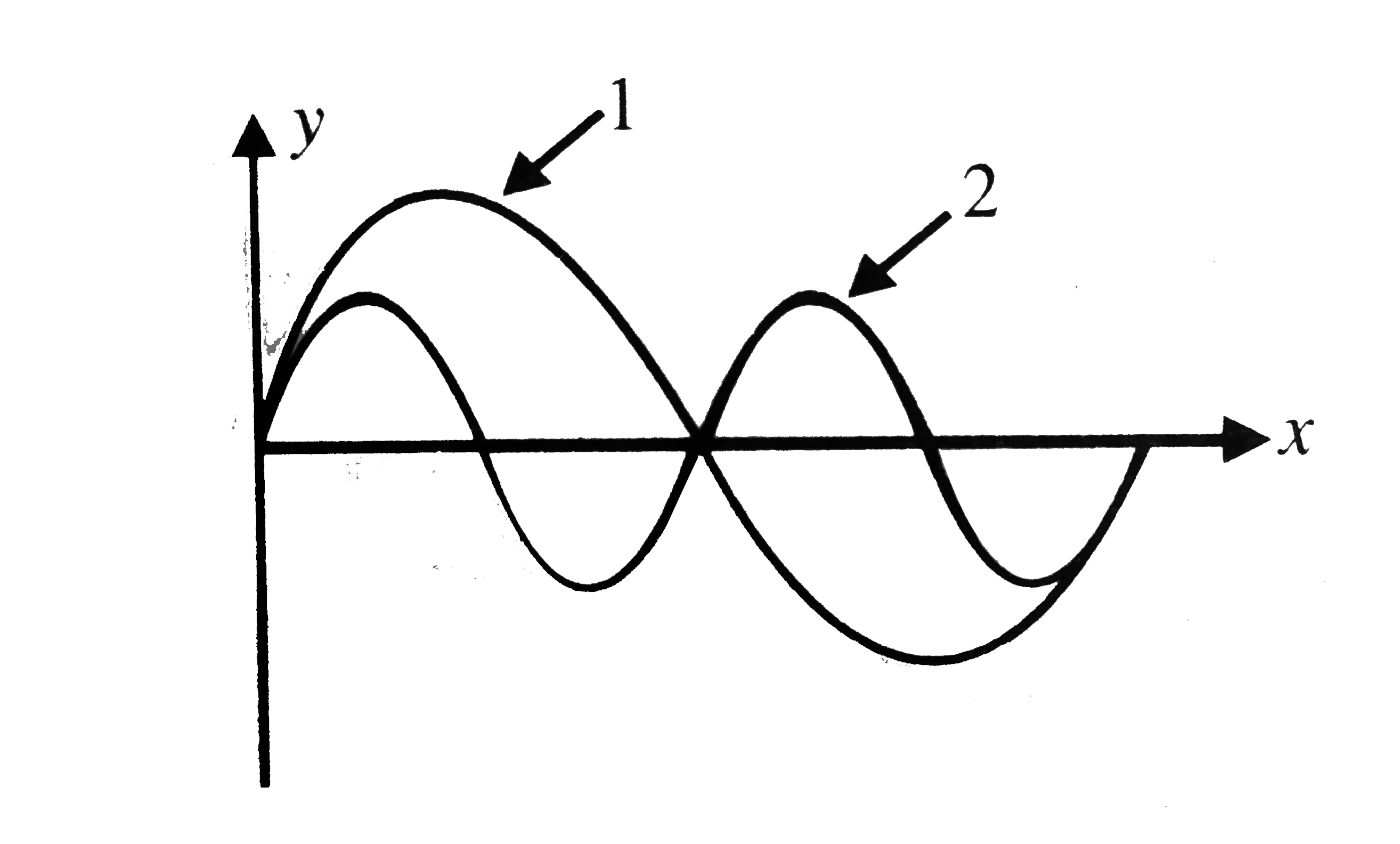
shows two snapshots, each of a wave travelling along a particular string. The phase for the waves are given by (a) 4x-8t (b) 8x-16t. Which phase corresponds to which waves in
View Solutionshows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.

(a) write down the equation of the curve. (b) find the angle θ made by the tangent at point P with the x-axis. (c ) If the particle at P has a velocity vpm/s, in the negative y-direction, as shown in figure, then determine the speed and direction of the wave. (d) find the frequency of the wave. (e) find the displacement equation of the particle at the origin as a function of time. (f) find the displacement equation of the wave.
View SolutionThe position of a transverse wave travelling in medium along positive x-axis is shown in figure at time t=0. Speed of wave is v=200 m/s
Frequency of the wave is

View Solutionin a sine wave ,positive of different particles at time t=0 is shown in figure. The equation for this wave if it is travelling along positive x -axis can be
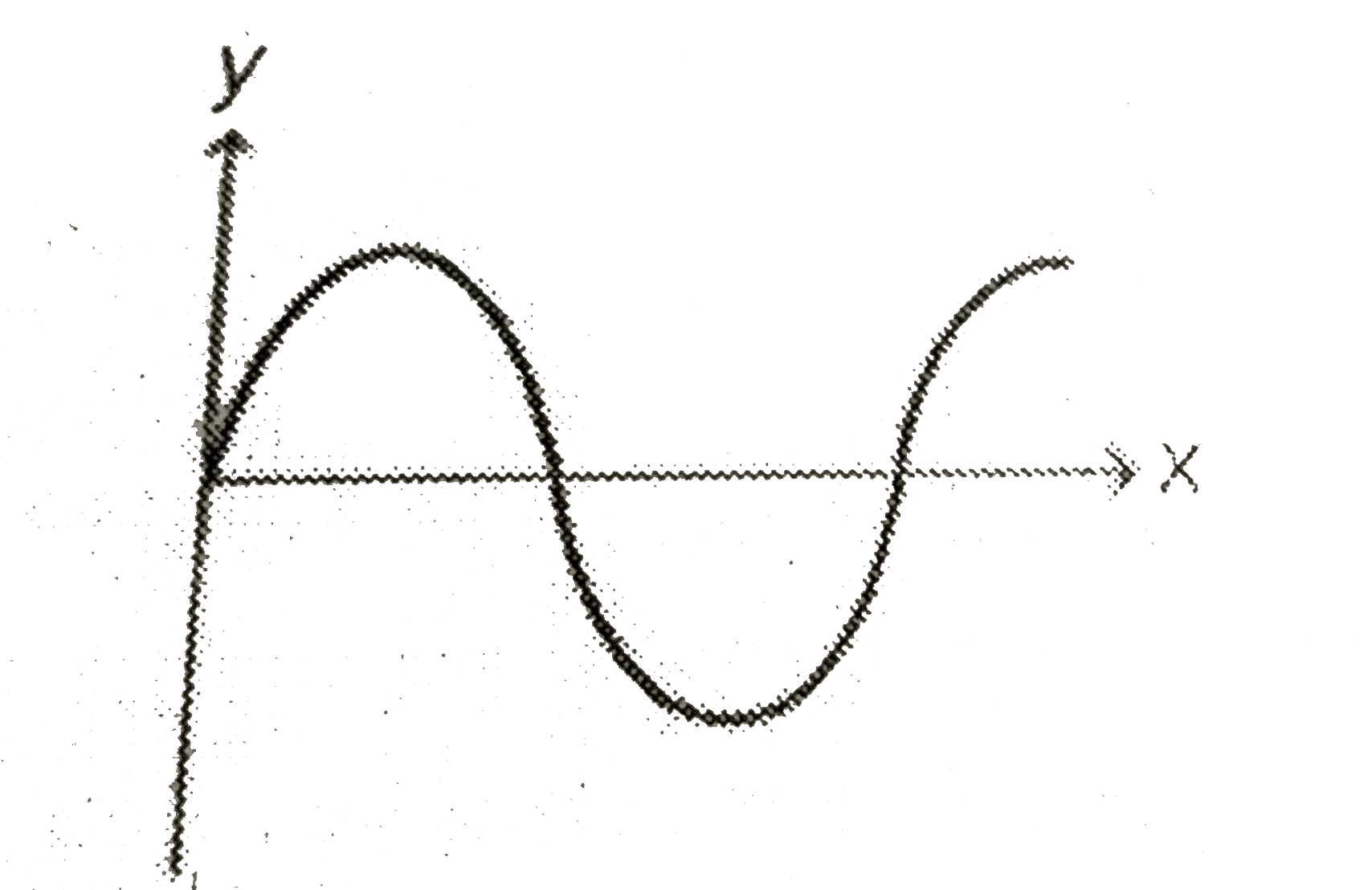
View Solution