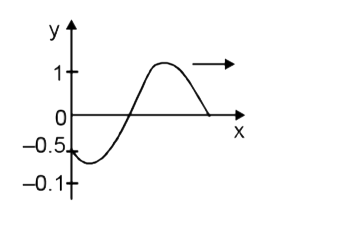
shows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.

(a) write down the equation of the curve. (b) find the angle $θ$ made by the tangent at point P with the x-axis. (c ) If the particle at P has a velocity $v_{p} m / s$ , in the negative y-direction, as shown in figure, then determine the speed and direction of the wave. (d) find the frequency of the wave. (e) find the displacement equation of the particle at the origin as a function of time. (f) find the displacement equation of the wave.

Video Solution

Text Solution

Verified by Experts

(a). From given curve: amplitude of the wave $A = 10 c m$ and wavelength $λ = 12 c m$
$y = A sin (k x \pm ω t + ϕ) = A sin (\frac{2 π}{λ} x \pm \frac{2 π}{T} t + ϕ)$ ….(i)
At $t = 0, y = A sin (k x + ϕ) = 10 \frac{sin (π)}{6} x + ϕ)$
At $x = 0, y = - 5 c m = 10 sin ϕ$
$sin ϕ = - (1) (2) \Rightarrow ϕ = - \frac{π}{6}$
hence $y = 0.10 (m) \frac{sin (π)}{6} x - \frac{π}{6})$
(b). $tan θ = \frac{d y}{d x} = 0.10 \times (π) (6) \frac{cos (π)}{6} x - \frac{π}{6})$
At $x = 6 m$
$\frac{d y}{d x} tan θ = \frac{π}{600 cos (π - \frac{π}{6}) = \frac{π}{60} (- \frac{cos (π)}{6})}$
$= - \frac{π}{60} . \frac{\sqrt{3}}{2} = \frac{- π \sqrt{3}}{120}$
$θ = {tan}^{- 1} (- \frac{π \sqrt{3}}{120})$
(c ). nParticle velocity
$v_{p} = v (\frac{d y}{d x})$
$- v_{p} = - v \frac{- π \sqrt{3}}{120})$
$v = \frac{- 120}{\sqrt{3 π}} v_{p} = \frac{- 40 \sqrt{3}}{π} v_{p}$ Along negative $x -$ axis.
(d). wave velocity
$v = f λ$
$\Rightarrow f = \frac{v}{λ 0 = \frac{40 \sqrt{3} v_{p}}{π \times 12}}$
$= \frac{10 \sqrt{3}}{3 π} v_{p} s^{- 1}$
(e). hence displacement equation of medium particle at origin at $x = 0$ , from eq... (ii)
$y = 10 (c m) sin [\frac{20 \sqrt{3}}{3} v_{p} t - \frac{π}{6}]$
(f). As wave is travelling towards negative x-directin hence positive sign should be used between kx and $ω t$ in eq. ..(i)
The equation of the wave,
$y = 0.1 (m) sin [\frac{π}{6} x (m) + ω t - \frac{π}{6}]$
here $ω = 2 π f = 2 π \frac{10 \sqrt{3}}{3 π} v_{p} = \frac{20 \sqrt{3}}{3} v_{p}$
Hence displacement equation of the wave
$y = 0.1 (m) sin [\frac{π}{6} x (m) + \frac{20 \sqrt{3}}{3} v - (p) t - \frac{π}{6}]$ ...(ii)

Updated on:21/07/2023

the equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by

A $sin (k x - ω t + \frac{π}{6})$
B $sin (k x - ω t - \frac{π}{6})$
C $sin (ω t - k x + \frac{π}{6})$
D $sin (ω t - k x - \frac{π}{6})$
The equation of a simple harmonic progressive wave along the negative direction of X-axis is
A $y = a sin 2 π [\frac{t}{T} - \frac{x}{λ}]$
B $y = a sin (2 π n t)$
C $y = a sin 2 π [\frac{t}{T} + \frac{x}{λ}]$
D $y = a cos 2 π [x]$
The equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by :-
.
A $sin (k x - ω t + \frac{π}{6})$
B $sin (k x - ω t - \frac{π}{6})$
C $sin (ω t - k x + \frac{π}{6})$
D $sin (ω t - k x - \frac{π}{6})$