A transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
Since the wave is travelling along +x−direction and the displacement of the end x=0 is at time t=0, the general equation of this wave is
y(x,t)=Asin{2πλ(vt−x1)}...(i)
where A=0.01m
when x=0.1m,y=−0.005m
Putting all values, we get −0.005=0.01sin{2πλ(vt−x1)}
where x1=0.1m
or, sin{2πλ(vt−x1}=−12
∴ Phase sintheta_(1)=2πλ(vt−x1)=7π6....(ii)
When x=0.2my=+0.005. therefore, we have
+0.005=0.01sin{2πλ(vt−x2)}
where x2=0.2m
θ2=2πλ(vt−x2)=π6 ......(iii)
From Eqs.(ii)and (iii)
Δθ=θ1−θ2=π
now, Δθ=2πλΔx
Thus, π=−2πλ(x1−×2)=−2πλ(0.1−0.2)
or λ=0.2m
Now, frequency g og the wave =frequency of the tuning for k=500Hz.
hence, wave velocity
v=fλ=500×0.2=100m/s
substituting for A,lambda and v in eq. (i) we get
y(x,t)=0.01sin(10π(100t−x))
this is the lequation of the wave where y and x are in metres and t in seconds.
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Single Correct
Explore 62 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Single Correct Answer
Explore 1 Video
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Exercise 5.2
Explore 23 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICSChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View Solution
Knowledge Check
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
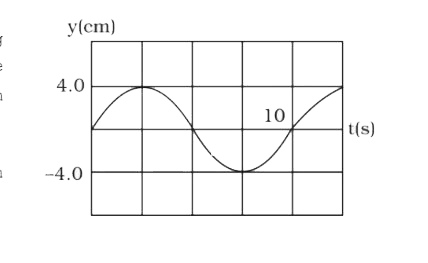
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?A−2cm/sB+2cm/sC+1.5cm/sD−2.5cm/sThe amplitude of S.H.M. at x=0.05 m is
A0.02 mB0.01 mC0.0141mD1.414 mA source of frequency 500Hz emits waves of wavelength 0.2m. How long does it take to travel 300m ?
A75 secondsB60 secondsC12 secondsD3 seconds
A transverse wave of frequency 500 Hz and speed 100 m/s is traveling in the positive x direction on a long string. At time t = 0 s the displacements at x=0.0 m and at x=0.25 m are 0.0 m and 0.02 m, respectively. The displacement at x=0.2 m at t=5×10−4s is
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
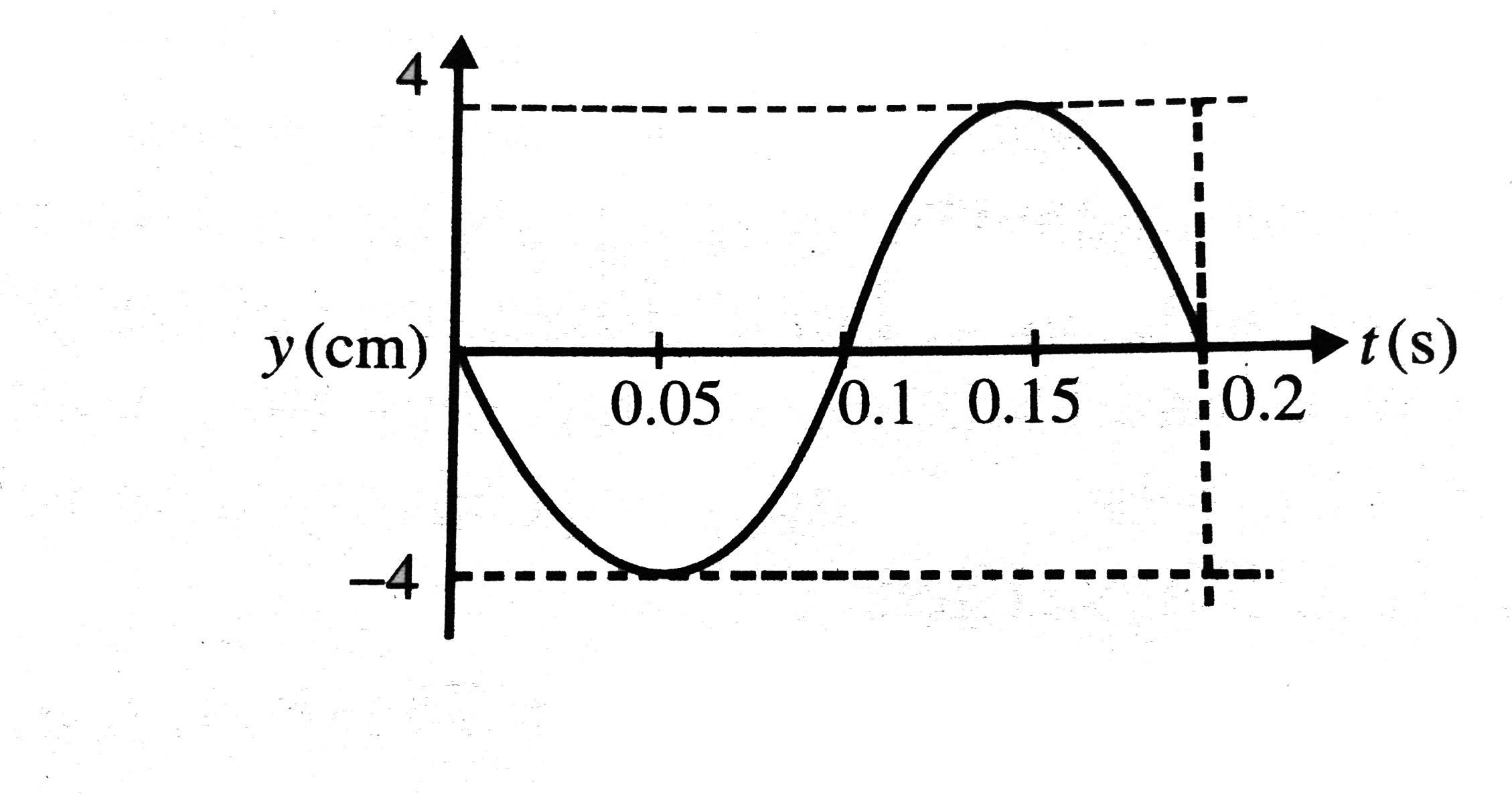
View SolutionThe displacement of a particle executing S.H.M is given by x=0.01sin100π(t+0.05). The time period is
View SolutionA simple harmoinc progressive wave of amplitude 0.05 m and frequency 5Hz is travelling along the positive direction of x-axis with a speed of 40 m/s, then the displacement of a particle at 30 m from origin in the time 1 second will be
View SolutionA source of frequency 500Hz emits waves of wavelength 0.2m. How long does it take to travel 300m ?
View Solution

