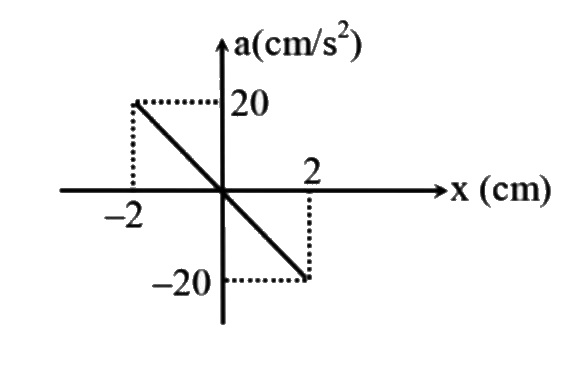
The acceleration-displacement $(a - X)$ graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

Video Solution

Text Solution

Verified by Experts

In SHM , $α = - ω^{2} x$
$β = - ω^{2} = (- α)$
$∴ β = ω^{2} = α$ (from graph)
and $ω = \sqrt{\frac{β}{α}}$
or $2 π f = \sqrt{\frac{β}{α}}$
or $f = \frac{1}{2 π} \sqrt{\frac{β}{α}}$

Updated on:21/07/2023

The velocity of a particle executing simple harmonic motion is
A $ω^{2} \sqrt{A^{2} + x^{2}}$
B $ω \sqrt{A^{2} - x^{2}}$
C $ω \sqrt{A^{2} + x^{2}}$
D $ω^{2} \sqrt{A^{2} - x^{2}}$
The acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
A $\frac{4 π}{\sqrt{3}} s$
B $\frac{2 π}{\sqrt{3}} s$
CThe given graph doesn't represent simple harmonic motion
Dinformation is insufficient
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.
BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.
Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.
Dits linear velocity and acceleration always attain their peak values simlataneaously.