In an LR circuit connected to a battery, the rate at which energy is stored in the inductor is plotted against time during the growth of current in the circuit. Which of the following best represents the resulation curve?
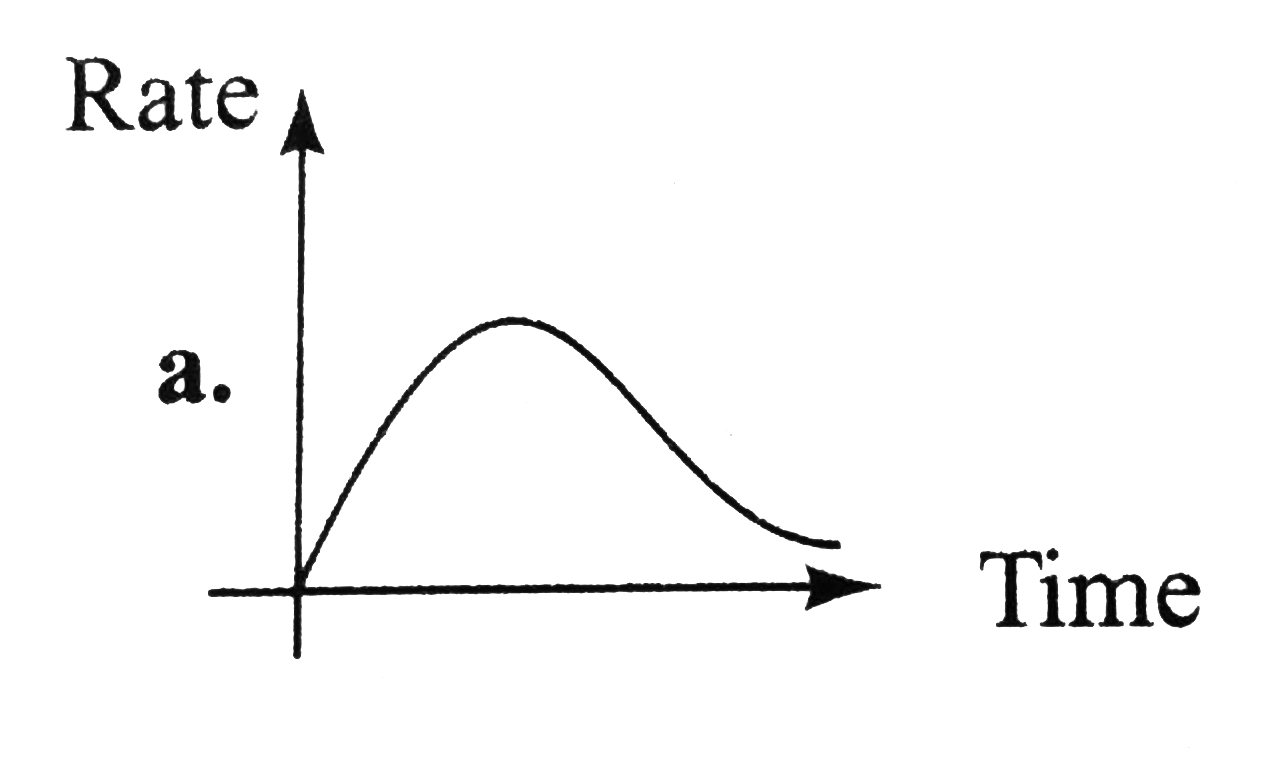
The correct Answer is:A
To solve the problem, we need to analyze the behavior of energy stored in an inductor in an LR circuit over time as the current grows. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Energy Stored in the Inductor
The energy (U) stored in an inductor is given by the formula:
U=12LI2
where L is the inductance and I is the current flowing through the inductor.
Step 2: Determine the Rate of Change of Energy
To find the rate at which energy is stored in the inductor, we need to differentiate the energy with respect to time (t):
dUdt=ddt(12LI2)
Using the chain rule, we get:
dUdt=LIdIdt
This expression indicates that the rate of change of energy depends on both the current (I) and the rate of change of current (dIdt).
Step 3: Analyze the Behavior at Initial and Final Times
- At t=0: The current I is zero, hence:
dUdt=L⋅0⋅dIdt=0
- At t=∞: The current reaches its maximum value I0, and the rate of change of current dIdt approaches zero as the circuit reaches steady state. Thus:
dUdt=LI0⋅0=0
Step 4: Sketch the Graph
From the analysis, we can conclude:
- The rate of energy storage starts at zero when t=0.
- It increases as the current increases and reaches a maximum value at some point during the growth of current.
- Finally, as the current stabilizes, the rate of energy storage returns to zero when t approaches infinity.
Step 5: Identify the Correct Graph
Based on the above behavior, the graph that best represents the rate of energy storage against time will start at zero, rise to a maximum, and then return to zero as time approaches infinity.
The correct option is Graph A, which shows this behavior.
The energy (U) stored in an inductor is given by the formula:
U=12LI2
where L is the inductance and I is the current flowing through the inductor.
To find the rate at which energy is stored in the inductor, we need to differentiate the energy with respect to time (t):
dUdt=ddt(12LI2)
Using the chain rule, we get:
dUdt=LIdIdt
This expression indicates that the rate of change of energy depends on both the current (I) and the rate of change of current (dIdt).
- At t=0: The current I is zero, hence:
dUdt=L⋅0⋅dIdt=0
- At t=∞: The current reaches its maximum value I0, and the rate of change of current dIdt approaches zero as the circuit reaches steady state. Thus:
dUdt=LI0⋅0=0
From the analysis, we can conclude:
- The rate of energy storage starts at zero when t=0.
- It increases as the current increases and reaches a maximum value at some point during the growth of current.
- Finally, as the current stabilizes, the rate of energy storage returns to zero when t approaches infinity.
Based on the above behavior, the graph that best represents the rate of energy storage against time will start at zero, rise to a maximum, and then return to zero as time approaches infinity.
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Knowledge Check
A simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
ARL In [√2√2−1]BLR In [√2−1√2]CLR In [√2√2−1]DRL In [√2−1√2]The rate of decay (R) of nuclei in a radioactive sample is plotted against time (t). Which of the following best represents the resulting curve ?
A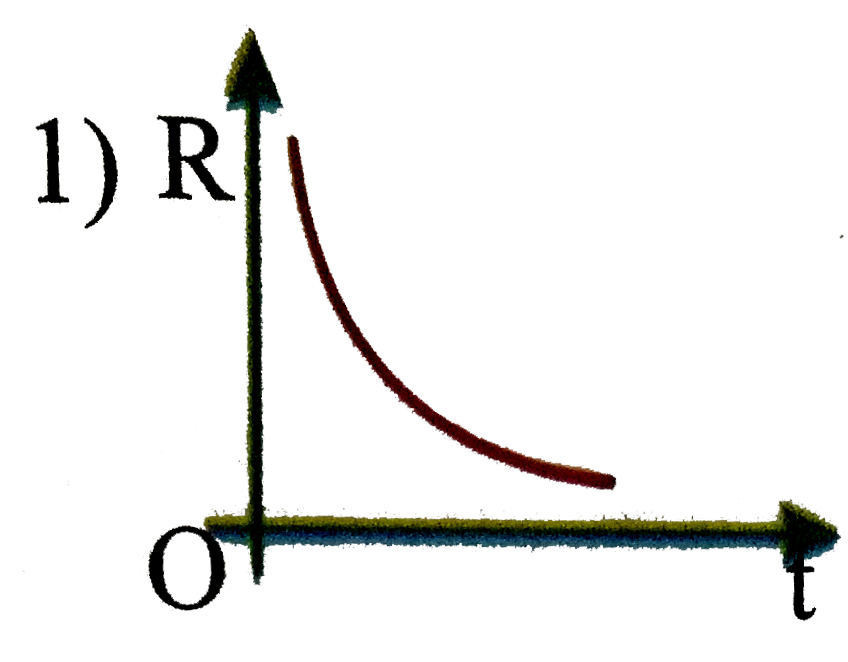 B
B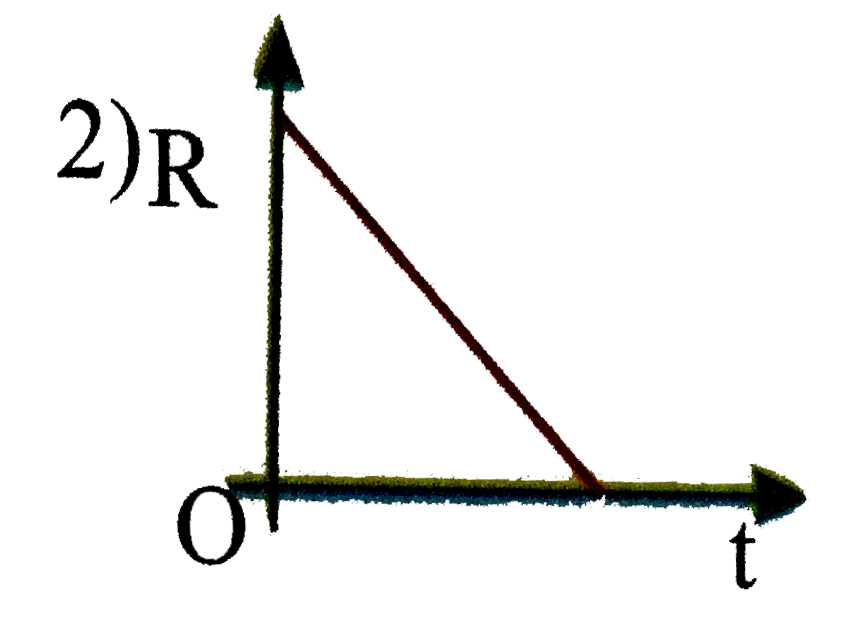 C
C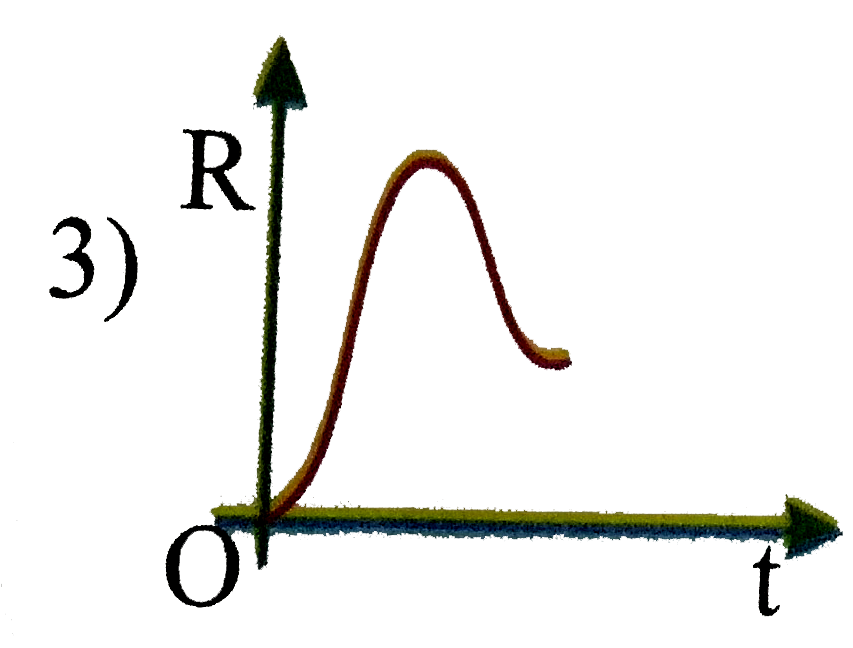 D
D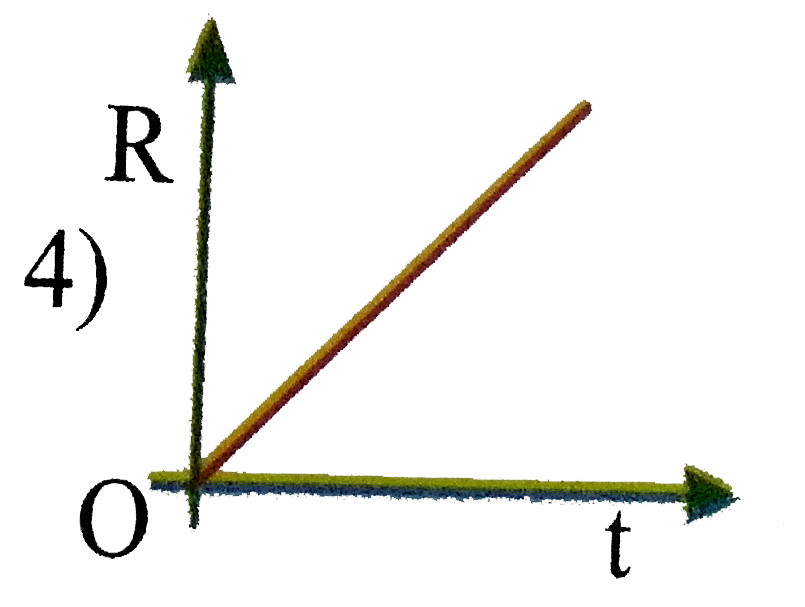
The rate of decay (R) of nuclei in a radioactive sample is plotted against time (t). Which of the following best represents the resulting curve ?
A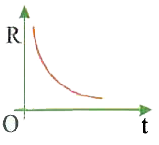 B
B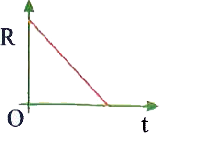 C
C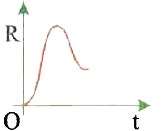 D
D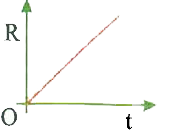
An ideal cell is connected to a capacitor through a voltmeter. The reading V of the voltmeter is plotted agains time. Which of the following best represents the resulting curve?
View SolutionIn an L-R circuit connected to a battery of constant emf E, switched is closed at time t=0. If denotes the induced emf across inductor and I the current in the circuit at any time t. Then which of the following graphs shown the variation of e with i?
View SolutionWhen an electric heater is switched on, the current flowing through it ( i ) is plotted against time ( t ). Taking into account the variation of resistance with temperature, which of the following best represents the resulting curve
View SolutionIf maximum energy is stored in capacitor at t = 0 then find the time after which current in the circuit will be maximum.
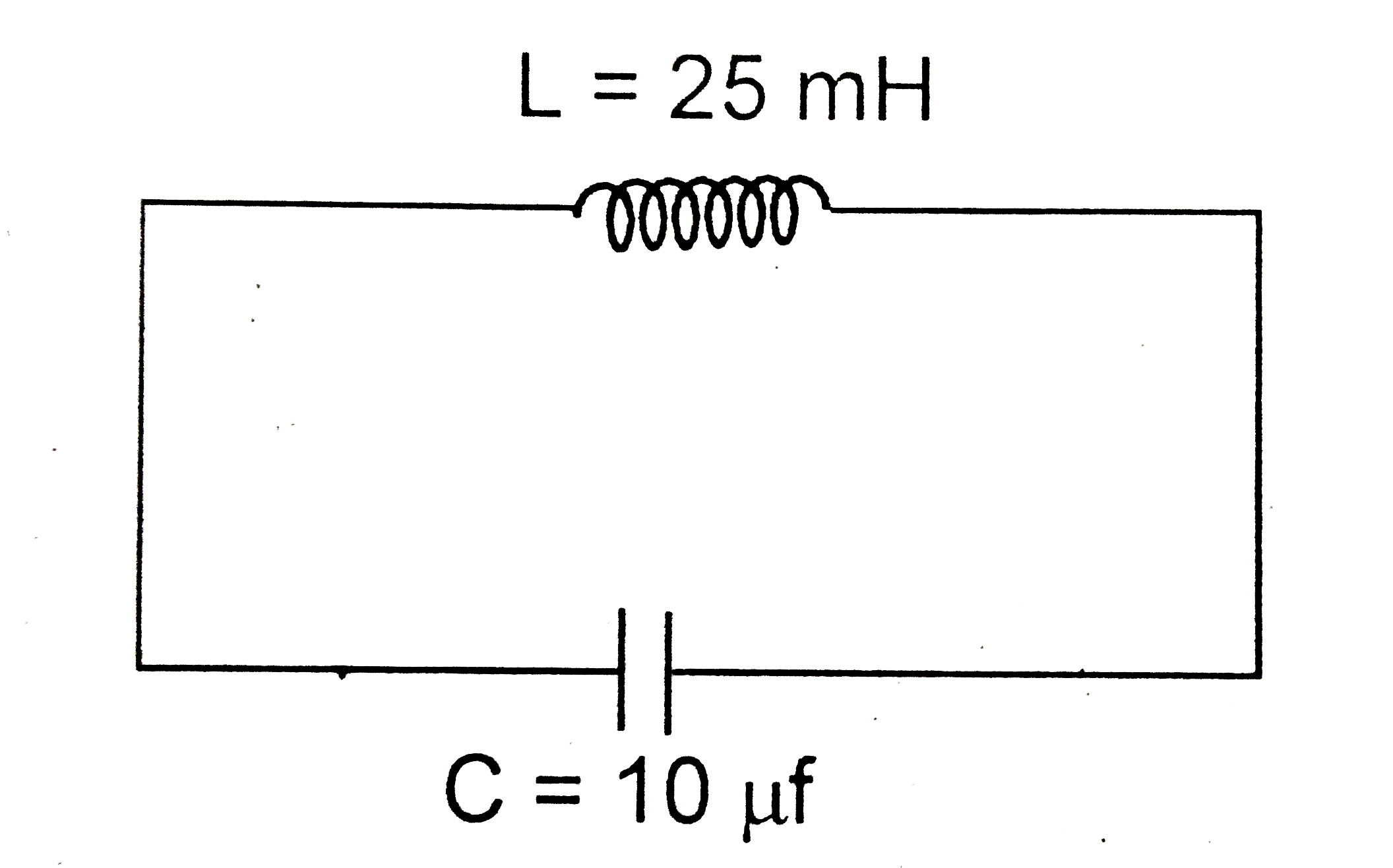
View SolutionAn inductor and a capacitor are joined in series to an AC source. The frequency of the AC is gradually increased. The phase difference φ between the emf and the current is plotted against nthe angular frequency ω. Which of the following best represents the resulting curve?
View Solution


_S01_061_Q01.png)