In Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is
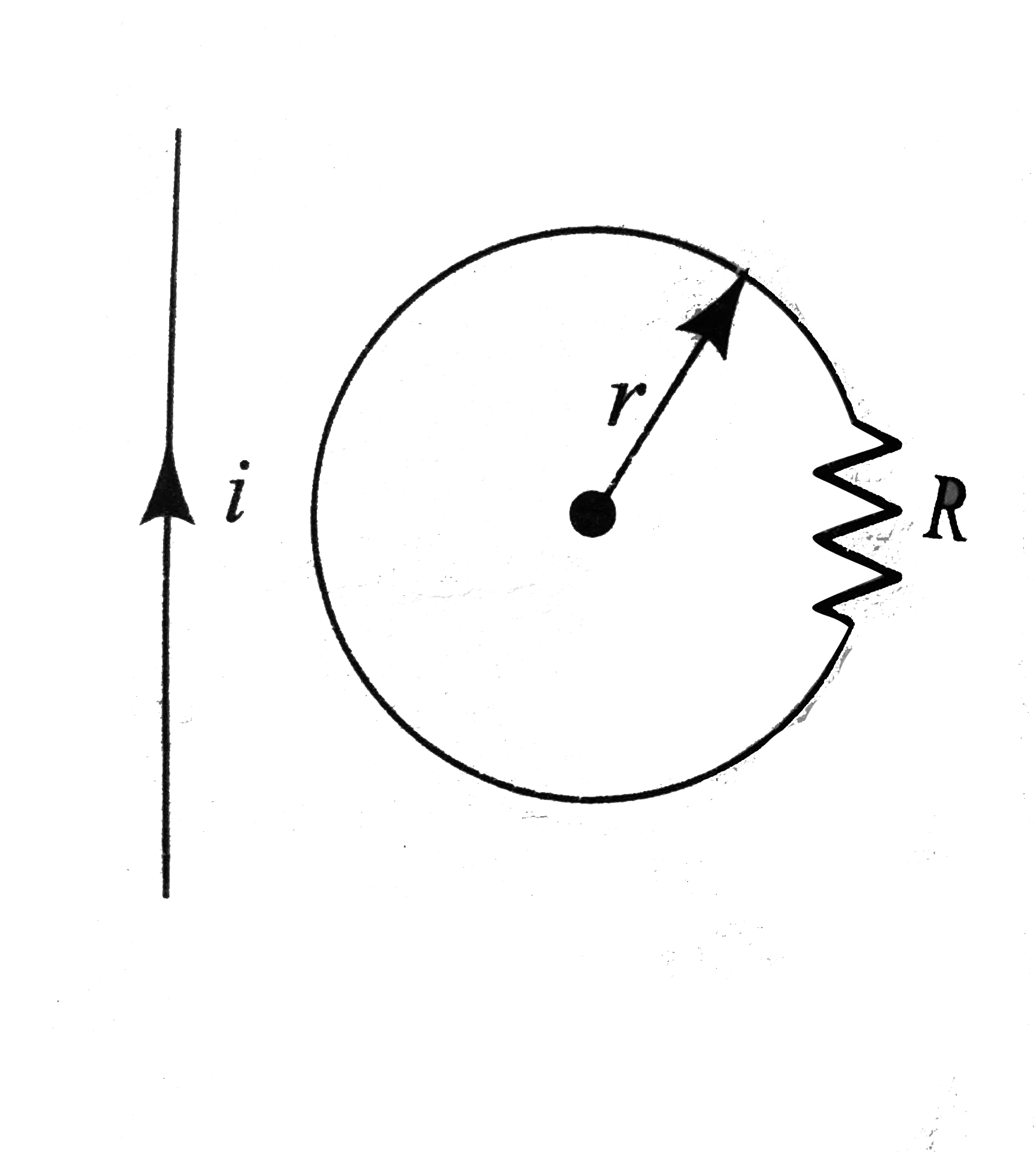
MaR
maRe−Rt/L
MRe−tR/L
MaR(1−e−tR/L)
The correct Answer is:D
E=Mdidt=Ma, I=MaR(1−e−tR/L)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
The current i in an induction coil varies with time t according to the graph

Draw the graph of induced e.m.f. with time.
View SolutionTwo coils, 1 & 2, have a mutual inductance = M and resistances R each. A current flows in coil 1, which varies with time as: I1=kt2, where K is a constant and 't' is time. Find the totalcharge that has flown through coil 2, between t=0 and t=T.
View Solution
Knowledge Check
In the adjacent figure, the mutual inducatance of the infinite straight wire and the coil is M, while the self inductance of the coil is L. The current in infinite wire is varying according to the realtion l1=αt, where α is a constant and t is the time. The time dependence of current in the coil is
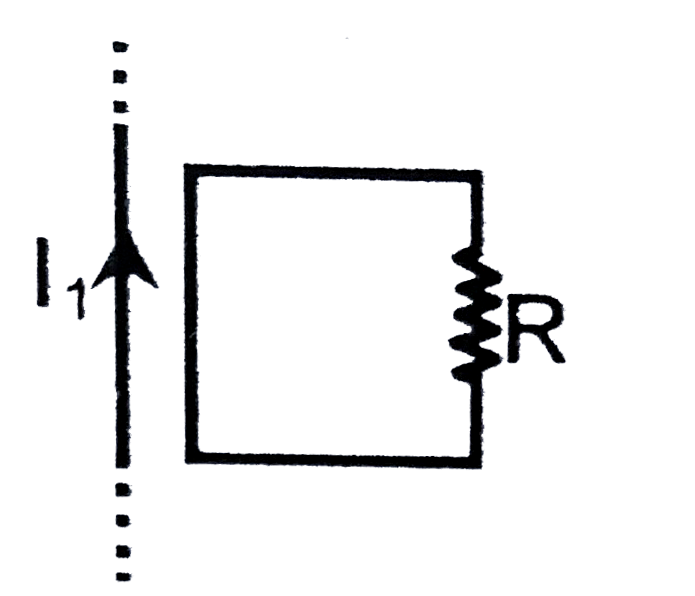 AMαRBMαLRe−Rt/LCαR(1−e−Rt/L)Dnone of these
AMαRBMαLRe−Rt/LCαR(1−e−Rt/L)Dnone of theseThe self-inductance of a coil is 2H. The current in the coil changes from 8A to 2.95 A in 0.01 s. The time constant of the coil will be -
A2sB0.1 sC10 msD1 msTwo coils have a mutual inductance of 0.01 H. The current in the first coil changes according to equation, I = 5 sin 200πt. The maximum value of emf induced in the second coil is
A10πVB0.1πVCπVD0.01πV
Two coils have a mutual inductance 0.005 H. The current changes in the first coil according to equation I=I0sinωt, where I0=10A and ω=100π rad/s. The maximum value of e.m.f. in the second coil is
View SolutionThe current i in an induction coil varies with time according to the graph shown in figure. Which of the following graph shows induced emf in the coil with time:
View SolutionMutual inductance of two coils depends on their self inductance L1 and L2 as :
View SolutionA coil resistance R and inductance L is connected to a battery of emf E volt. The final current in the coil is
View SolutionThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
View Solution