There is a uniform magnetic field B in a circular region of radius R as shown in Fig. 3.149 whose magnitude changes at the rate of dB/dt. The emf circular concentric conducting arc of radius R1 having an angle θ as shown (−OAO'=θ) is

(a) θ2πR21dBdt
(b) θ2R2dBdt
(a) θ2πR2dBdt
(d) none of these
The correct Answer is:B
( b) Rquired emf
f=(πR2dBdt)θ2π=R2θ2(dBdt)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A uniform magnetic field B exists in a circular region of radius R. the field is perpendicular to the plane and is increasing at a constant rate of dBdt=α. There is a straight conducing rod AB of length 2R. Find the emf induced in the rod when it is placed as shown in figure (a) & (b). Point C is midpoint of the rod in figure (b)
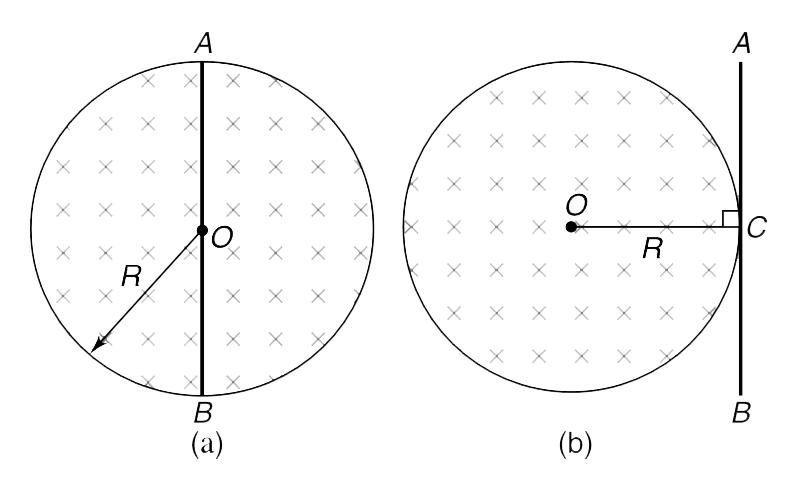
View SolutionA uniform magnetic field is applied in a circular region of radius R as shown in the given figure. A charged particle of charge q and mass m enters with a velocity from point P along the line that is making an angle with the line segment OP, in the region of magnetic field.
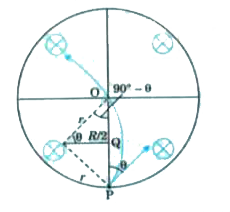
The charged particle is found to pass through the centre of the circular region. Find the angle θ.
Given : B=1T,R=10cm,m=6×10−3kg,q=6×10−2C,v=1/√3.
View Solution
Knowledge Check
Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.
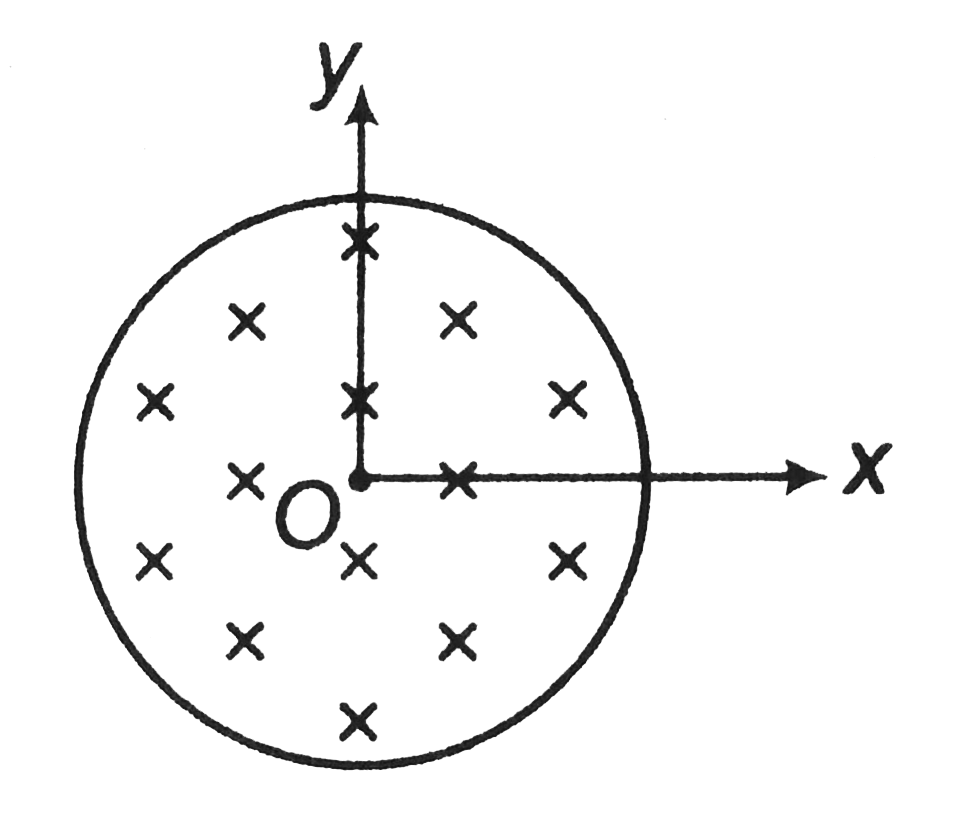 Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axis
Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axisThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
Athe emf induced in the ring is πr2dBdtBthe emf induced in the ring is 2πrdBdtCdiametrically opposite points on the ring are at the same potentialDall points on the ring are at the same potentialA particle of charge q and mass m is projected with a velocity v0 toward a circular region having uniform magnetic field B perpendicular and into the plane of paper from point P as shown in Fig. 1.136. R is the radius and O is the center of the circular region. If the line OP makes an angle θ with the direction of v0 then the value of v0 so that particle passes through O is
 AqBRmsinθBqBR2msinθC2qBRmsinθD3qBR2msinθ
AqBRmsinθBqBR2msinθC2qBRmsinθD3qBR2msinθ
There is a uniform magnetic field (B) perpendicular to the plane of the figure in a circular region of radius a centred at O. ABCD is a conducing loop in the plane of the figure with its arms BC and DA along two radial lines from O having an angle θ between them. AB is circular arc of radius OB = d centred at O. CD is also a circular arc of radius OC=b centred at O. The magnetic field is changed at a rate dBdt.
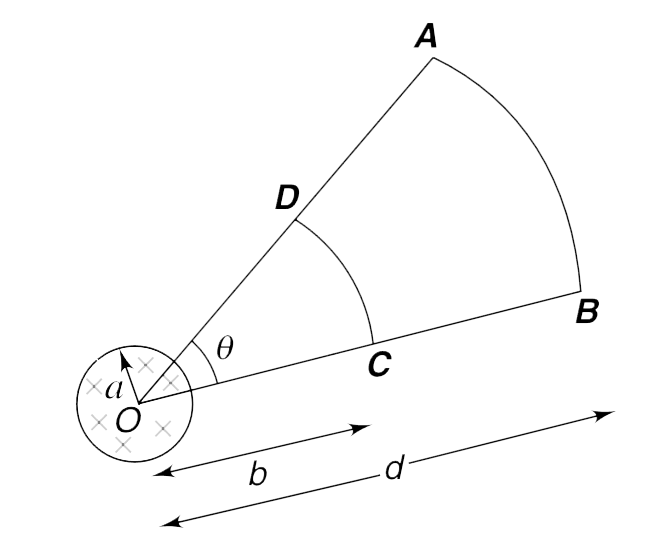
(a) The emf induced in the loop ABCD.
(b) Find emf induced in arc AB.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionIn a very long solenoid of radius R, if the magnetic field chabges at the rate of dB/dt.AB=BC
The induced emf for the trianglar circuit ABC shown in Fig. 3.196 is

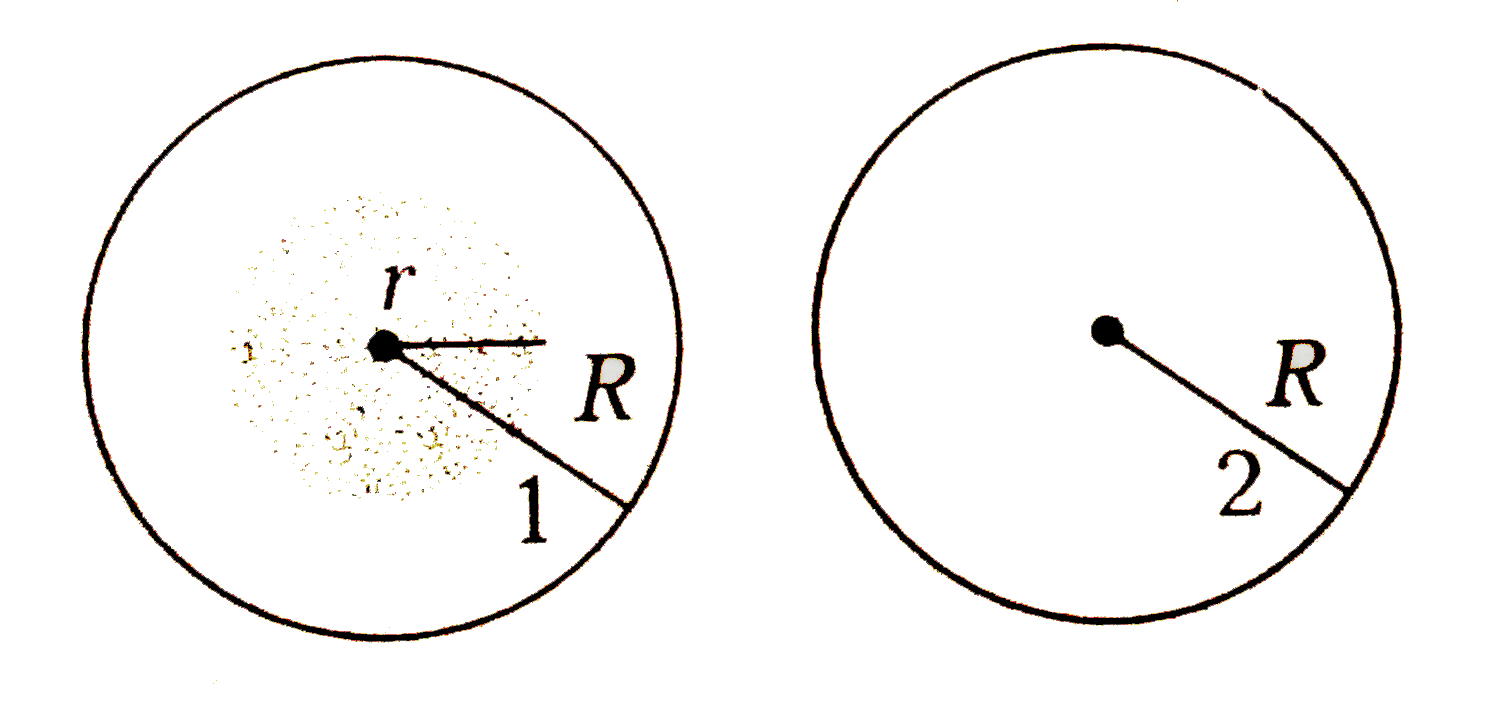
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
View Solution
