A magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of the generated in the loop during that time
(a) aT3R
(b) a2T23R
( c) a2T2R
( d) a2T33R
The correct Answer is:D
(D) Given that ϕ=at(T−t)
Induced emf, E=dϕdt=ddt[at(T−t)]
=at(0−1)+a(T−t)
=a(T−2t)
So, induced emf is also a function of time.
∴ Heat generated in time T is
H=∫T0E2Rdt=a2R∫T0(T−2t)2dt=a2T33R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A magentic flux through a statinary loop with a resistance R varies during the tiem interval τ as Φ=at(τ−t). Find the amount of heat generated in the loop during that time. The inductance of the loop is to be neglected.
View SolutionThe magnetic flux through a stationary loop with a resistanoe R varies during interval of time T as ϕ= at (T−t). If the heat generated during this time, neglecting the inductance of the loop, is a2T3pR, then find p.
View Solution
Knowledge Check
The magnetic flux through a stationary loop with resistance R varies during interval of time T as ϕ = at (T – t). The heat generated during this time neglecting the inductance of loop will be
Aa2T33RBa2T23RCa2T3RDa2T3RThe magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by
AQ=1R.ΔϕΔtBQ=ΔϕRCQ=ΔϕΔtDQ=R.ΔϕΔtThe magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by
AQ=1RΔϕΔtBQ=ΔϕRCQ=ΔϕΔtDQ=R.ΔϕΔt
The electrodes of a capacitor of capacitance C=2.00μF carry opposite charges q0=1.00mC. Then the electores are interconnected through a resistanace R=5.0MΩ. Find:
(a) the charge flowing thorugh that resistance during a time interval τ=2.00s,
(b) the amount of heat generated in the resistance during the same interval.
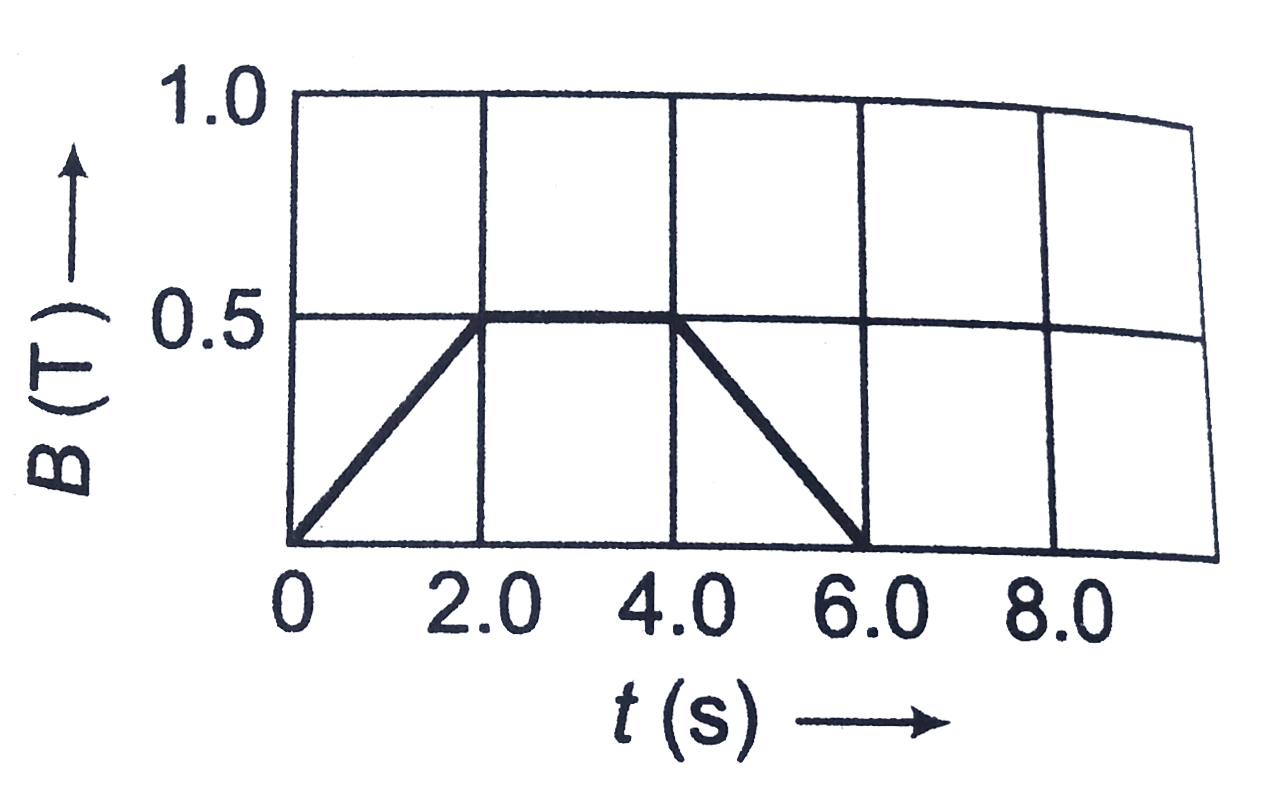
View SolutionThe magnetic field through a single loop of wire, 12cm in radius and of 8.5Ω resistance, changes with time as shown in figure. Calculate the emf in the loop as a function of time. Consider the time intervals
(a) t=0 to t=2.0s (b) t=2.0s to t=4.0s (c) t=4.0s to t=6.0s.
The magnetic field is perpendicular to the plane of the loop.
View SolutionThe magnetic flux in a closed circuit of resistance 10Ω varies with time according to equation , ϕ=6t2−5t+1. What is the magnitude of the induced current at t=0.25s?
View SolutionThe magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represent by
View SolutionThe magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
View Solution
