The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
0.12 V
2.4 V
0.02 V
1.2 V
The correct Answer is:C
Given, ϕ=(2t2+4t+6)mWb
AS, ε=dϕdt=ddt(2t2+4t+6)×10−3Wbs−1
=(4t+4)×10−3V
At t=4s
ε=(4×4+4)×10−3V=20×10−3=0.02V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:Lenz'S Law And Conservation Of Energy
Explore 13 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:MCQs
Explore 2 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:Magnetic Flux
Explore 3 Videos
- ELECTRIC CHARGES AND FIELDSBook:NCERT FINGERTIPSChapter:ELECTRIC CHARGES AND FIELDSExercise:Assertion And Reason
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(5t2+10t+5) milliweber. Calculate the e.m.f. induced in the loop at t=5 s.
View SolutionThe magnetic flux passing perpendicular to the plane of the coil and directed into the paper is varying according to the relation ϕ=3t2+2t+3, where ϕ is in milliweber and t is in second. Then the magnitude of emf induced in the loop when t=2 second is-

View Solution
Knowledge Check
The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation ϕ=(2t2+4t+6)mWb. The emf induced in the loop at t=4 s is
A0.12 VB2.4 VC0.02 VD1.2 VIn the figure the flux through the loop perpendicular to the plane of the coil and direciton into the paper varying according to the relation ϕ=6t2+7t+I where ϕ is in milliweber and t is in loop at t=2s and direction of induced current through R are
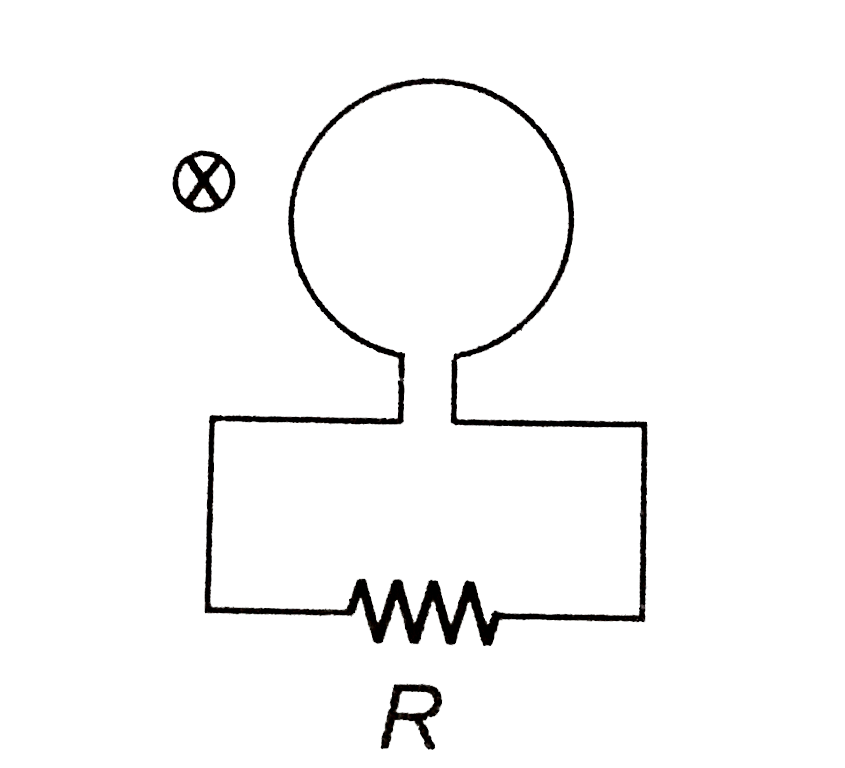 A39mV , right to leftB39mV , left to rightC31mV right to leftD31mV , left to right
A39mV , right to leftB39mV , left to rightC31mV right to leftD31mV , left to rightThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first
 Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)
The magnetic flux passing prependicular to the plane of the coil directed into the paper is varying according to the relation
ϕ=6t2+8t+I0 , where ϕ is in weber and t in second.
(a) What is the magnitude of emf induced in the loop when t=2sec ?
(b) What is the magnitude and direction of current at t=2sec ?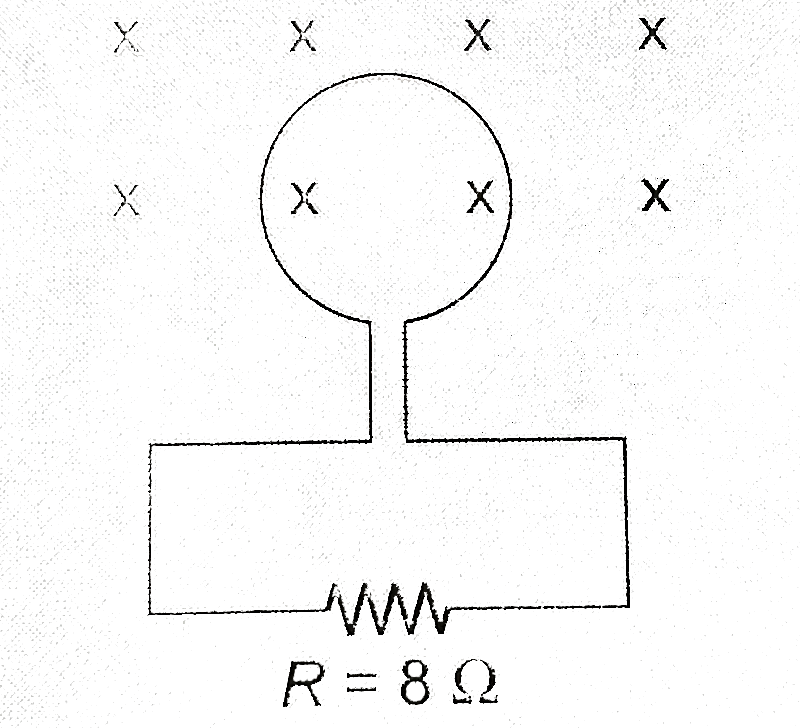
View SolutionThe magnetic flux through a coil is varying according to the relation ϕ=(5t3+4t2+2t−5) Wb. Calculate the induced current through the coil at t=2 s if resistiance of coil is 5 ohm.
View SolutionThe magnetic flux through a loop is varying according to relation ϕ=6t2+7t+1 where ϕ is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second ?
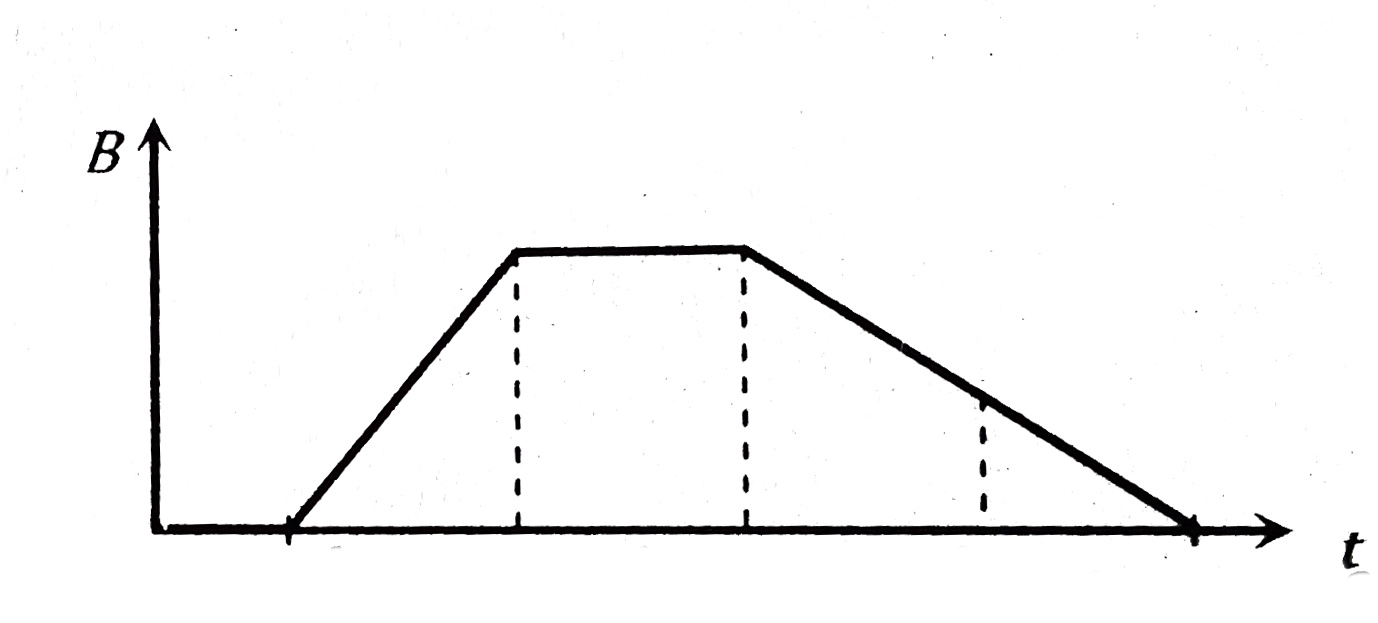
View SolutionThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.

View SolutionThe graph gives the magnitude B (t) of a uniform magnetic field that exists throughout a conducting loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first
View Solution

