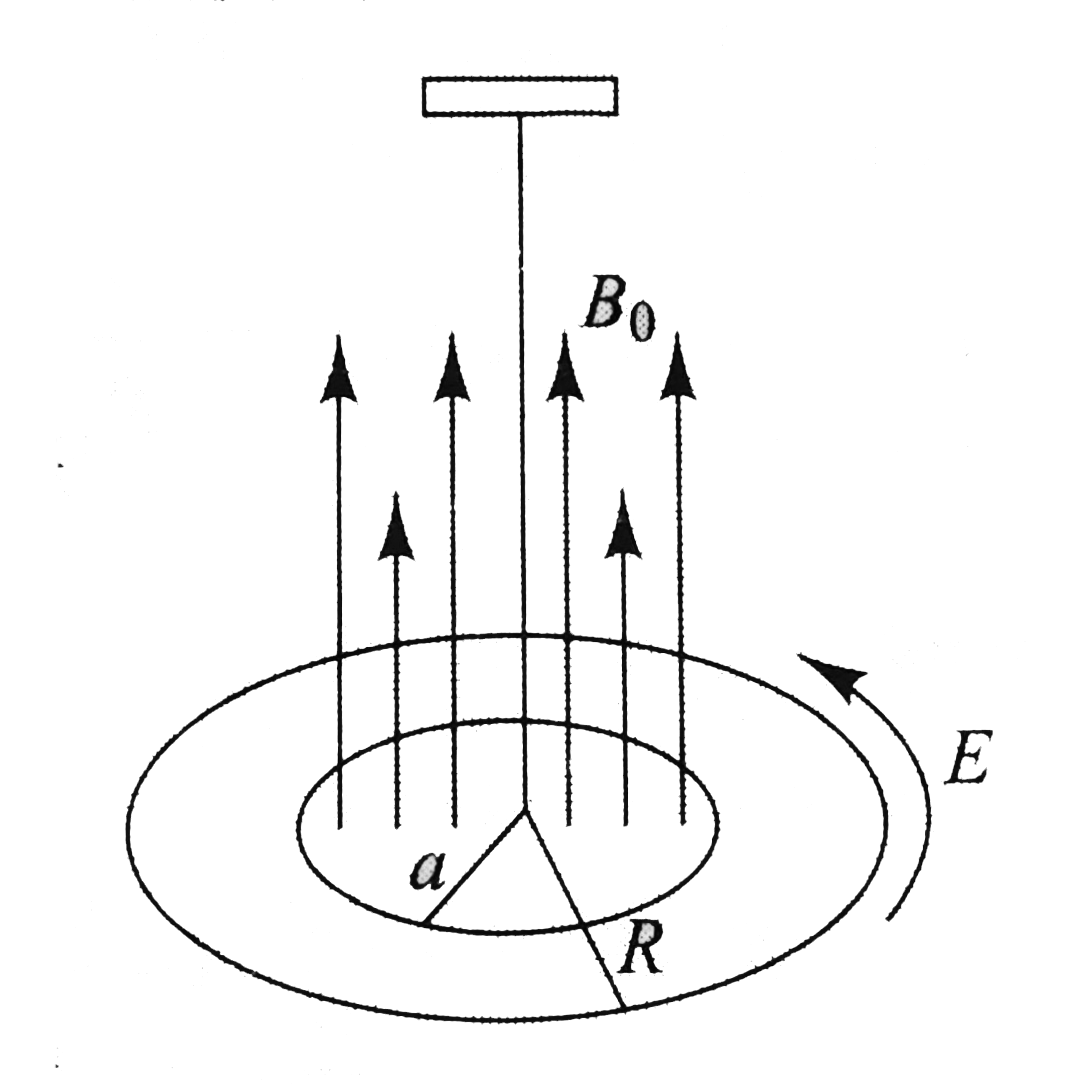
A line charge with linear charge density $λ$ is wound around an insulating disc of mass $M$ and radius $R$ , which is then suspended horizontally as shown in Fig. 3.90, so that it is free to rotate. In the central region, of radius $a$ , there is a uniform magnetic field $B_{0}$ , pointing up. Now the magnetic field is switched off, which causes the disc to rotate.
Find the angular speed with which the disc starts rotating.

Video Solution

Text Solution

Verified by Experts

The induced electric field $E$ due to the changing magnetic field is given by (from Faraday's law)
$\to$ $E . 2 π r = - π a^{2} \frac{d B}{d t}$ $\to$ $E = \frac{- a^{2}}{2 R} \frac{d B}{d t}$
Hence, induced electric field is tangential to the disc as shown in Fig. 3.90 and its magnitude is $E = \frac{a^{2}}{2 R} \frac{d B}{d t}$ .
This electric field causes the disc to rotate. Now torque on the disc is $τ = (λ p u R) E R = π l a m b d a^{2} R \frac{d B}{d t}$ .
Angular impulse:
$L = \int τ d t = \int π λ a$ ^(2)R(dB)/(dt)dt = pi $λ$ a^(2)Rint dB = pi alpha a^(2)RB_(0) $< b r > N o w$ L = Iomega $< b r >$ rarrpi $λ$ a^(2)RB_(0) = (MR^(2))/(2)omegararromega = (2pi lambda a^(2)B_(0))/(MR)

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A nonconducting ring of uniform mass m, radius b and uniform linear charge density $λ$ is suspended as shown in figure in a gravity free space. There is uniform coaxial magnetic field $B_{0}$ , pointing up in a circular region of radius 'a' $(< b)$ . Now if this field is switched off, then:-

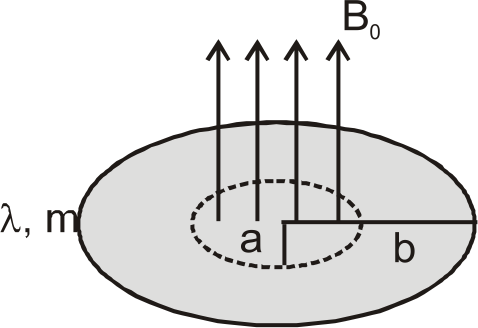AThere will be induced electric field on periphery of ring, in anticlockwise sense when seen from above
BInduced electric field imparts angular momentum of magnitude $λ π a^{2} b B_{o}$
CFinal angular velocity of ring will be more if time taken to switch of the field $B_{o}$ is small
DFinal angular velocity will always be independent of time taken to switch off the field $B_{o}$
Question 2 - Select One
Charge $Q$ is uniformly distributed on the rim of a thin insulating disc of mass $m$ which is initially at rest and placed on a smooth horizontal surface. What will be the angular velocity of the disc if a magnetic field $B$ , perpendicular to the plane of the disc is switched on ?

A $Q B / 2 m$
B $Q B / 3 m$
C $2 Q B / 3 m$
D $Q B / m$
Question 3 - Select One
A ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is:
A $\frac{q B}{m}$
B $\frac{2 q B}{m}$
C $\frac{q B}{2 m}$
DNone of these

CENGAGE PHYSICS-ELECTROMAGNETIC INDUCTION-compression type

Home
Ask Doubt
Profile