A particle of mass m and charge q is moving in a region where uniform, constant electric and mangetic fields →Eand→B are present. →Eand→B are parallel to each other. At time t=0, the velocity →v0 of the particle is perpendicular to →E (Assume that its speed is always <<c, the speed of light in vacuum). Find the velocity →v of the particle at time t. You must express your answer in terms of t,q,m, the vector →v0,→E and →B and their magnitudes →v0,→E and →B.
ˆj=→EE or →BB,ˆi=→v0v0,ˆk=→v0×→B0v0B
Force due to electric field will be along y-axis. Magnetic force will not affect the motion of changed particle in the direction of electric field (or y-axis) so.
ay=Fem=qEm,vy=ayt
=qEmT....(i)

The changed particle under the action of magnetic field describes a circle in x-z plane (perpendicular to →B) with T=2πmBq or ω=2πT=qBm
Initially (t=0) velocity was along x-axis. Therefore, magnetic force (→Fm) will be along positive z-axis [→Fm=q(→v0×→B)]. Let it this force makes an angle θ with x-axis at time t, then
θ=ωt
∴vx=v0cosωt=v0cos(qBmt)...(ii)
vz=v0sinωt=v0sin(qBmt)...(iii)
From Eqs. (i), (ii) and (iii)
→v=vxˆi+vyˆj+vzˆk
∴→v=v0cos(qBmt)(→v0v0)+qEmt(→EE)+v0sin(qBmt)(→v0×→Bv0B)
Or →v=cos(qBmt)(→v0)+(qmt)(→E)+sin(qBmt)(→v0×→BB)
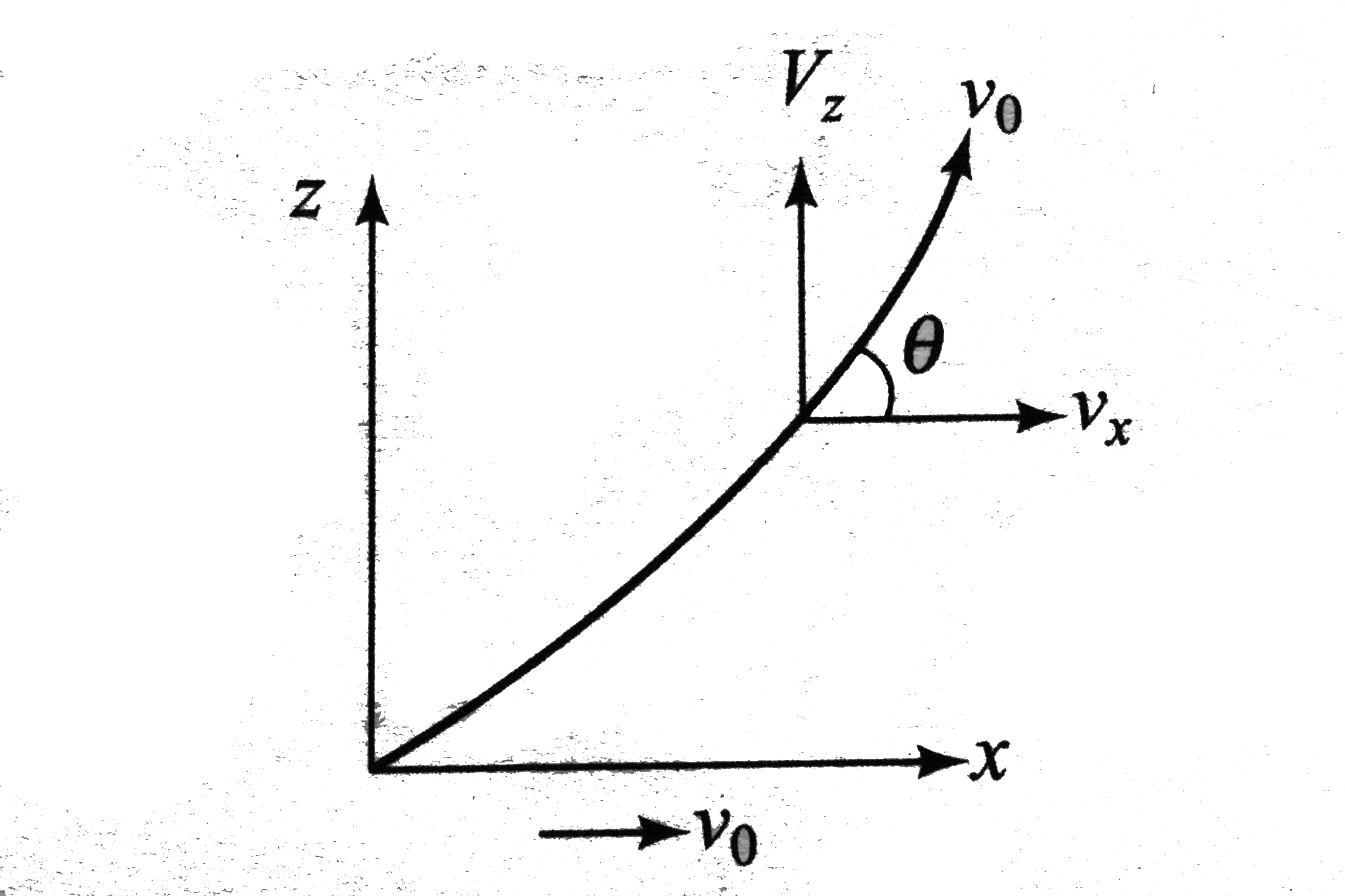 .
.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
Knowledge Check
A particle of charge q and mass m starts moving from the origin under the action of an electric field →E=E0ˆi and →B=B0ˆi with a velocity →v=v0ˆj. The speed of the particle will becomes √52v0 after a time
Amv0qE0Bmv02qE0C√3mv02qE0D√5mv02qE0
A particle of mass m and charge q is moving in a region where uniform electric field −−→E and and uniform mag-netic field −−→Bare present. It is given that −−→E∣∣→E∣∣=−−→B∣∣→B∣∣. At time t = 0, velocity of the particle is −−→V0 and −−→V0.−−→E=0. Write the velocity of the particle at time t.
View SolutionAn electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionIf ∣∣→a+→b∣∣=∣∣→a−→b∣∣, show that the vectors →aand→b are perpendicular to each other.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
View SolutionIf →a+→b+→c=→0, −→|a|=3, ∣∣→b∣∣=5 and |→c|=7.
Find the angle betweeen →a and →b
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionTwo vectors →a and →b are perpendicular to each other if →a.→b=0.
View Solution
