In fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
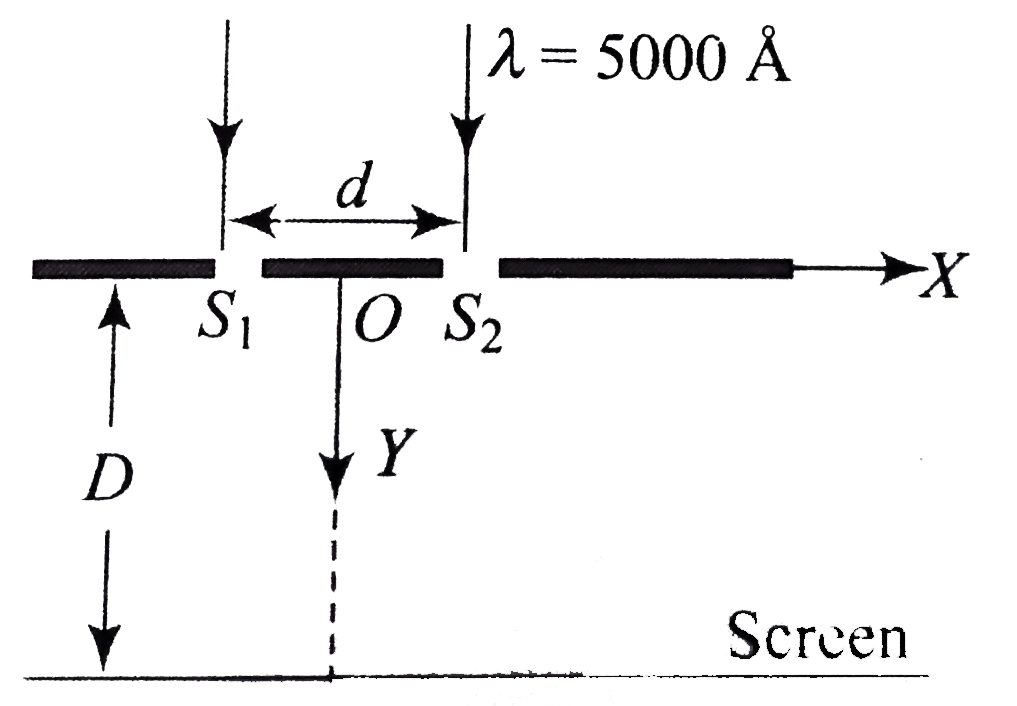
The velocity of central maxima at t=5s is
50ms−1 along Y-axis
50ms−1 along negative Y-axis
25ms−1 along Y-axis
3×108ms−1 along Y-axis
The correct Answer is:a
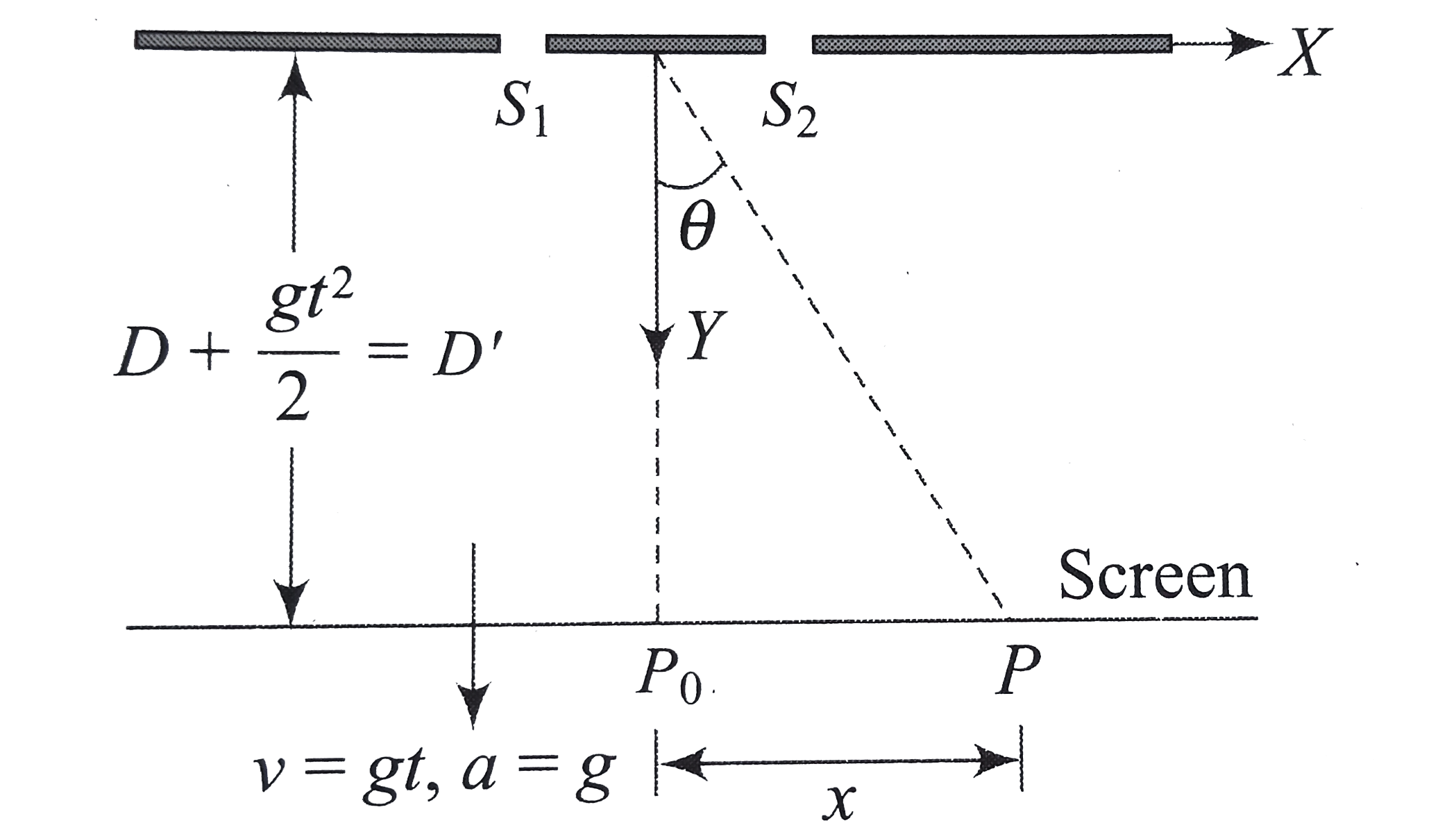
At any time t, the situation ia as shown in the figure below.
Central maxima is always lying on y-axis at P0. Its velocity at any time t is given by v p gt along positive Y-axis. So, required velocity is 50ms−1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives4videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK34videos
THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK38videos
WAVES
Similar Questions
Light of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View SolutionLight of wavelength 6000 o A is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. find the position of the first dark fringe
View Solution
Knowledge Check
- Question 1 - Select One
In fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
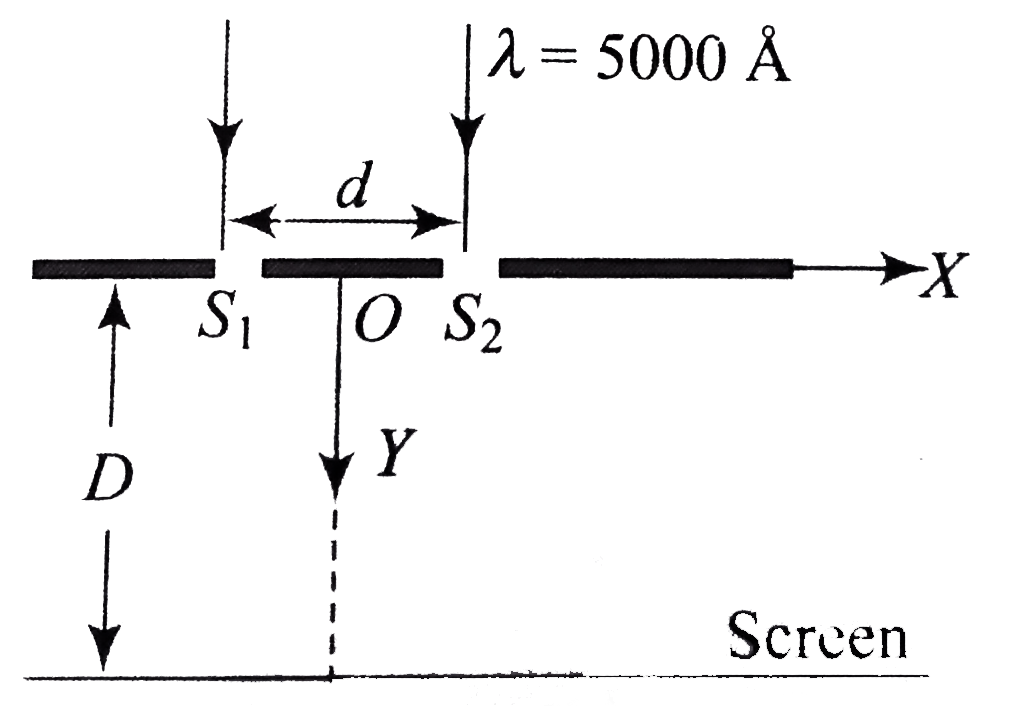
Velocity of 2nd maixma w.r.t central maxima at t=2s isA(8cms−1)ˆi+20ms−1ˆjB8cms−1ˆiC2cms−1ˆiD86ms−1ˆi - Question 2 - Select One
In fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
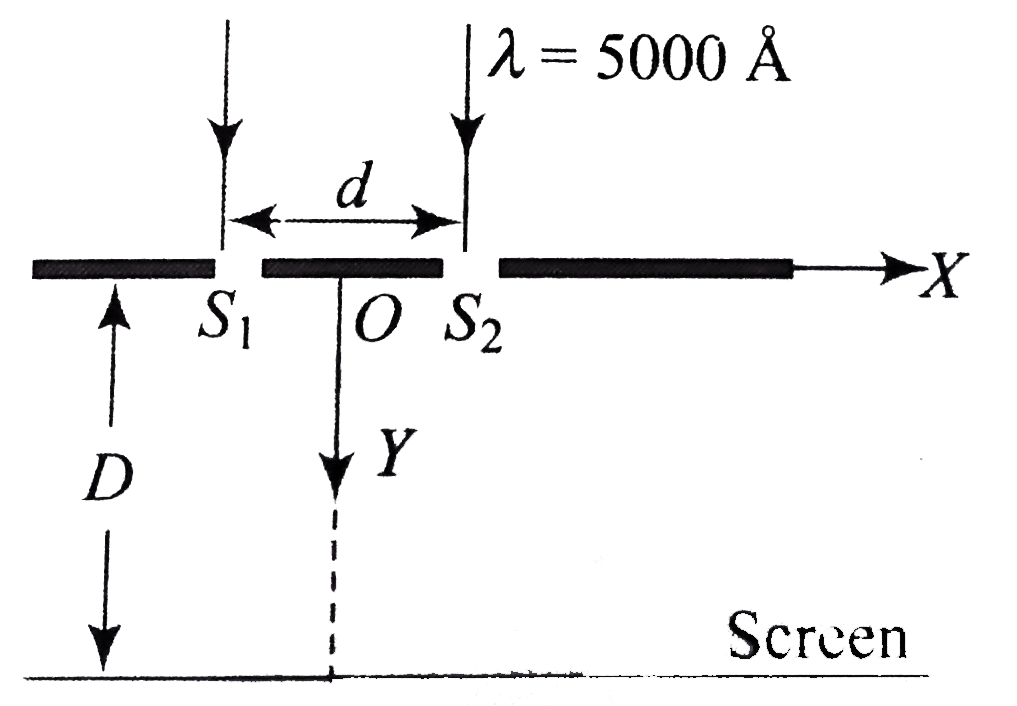
Acceleration of 3rd maxima w.r.t. 3rd maxiam on other side of central maxima at t=3 s isA0.02ms−1ˆiB0.03ms−1ˆiC10ms−1ˆjD0.6ms−2ˆi - Question 3 - Select One
Light of wavelength 5000Å is incident over a slit of width 1μm. The angular width of central maxima will be
A30∘B60∘C90∘D120∘
Light of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
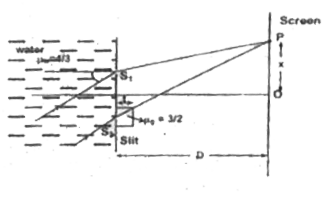
View SolutionA coherent beam light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1 m from the slits and the separation between- the slits is 3×10−4m. A thin film of glass μg= 3/2 and thickness 0.41 mm is placed near one slit as shown in the figure, find
(a) the position of central maxima.
(b) the intensity at'point O.
View SolutionIn YDSE monochromatic light of wavelength 600 nm incident of slits as shown in figure.
_PHY_E01_002_Q01.png)
If S1S2=3mm,OP=11mm thenView SolutionLight of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
View SolutionLight of wavelength 5000Å is incident normally on a slit. The first minimumof the diffraction pattern is formed at adistance of 5 mm from centra maximum. The screen is situated at a distance of 2 m from the slit. The slit width is
View Solution