When light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
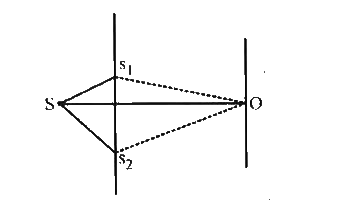
If the slits S1 and S2 are arranged as shown in Fig. the ratio of internsity of fringe at P and R is

0
∞
1:1
1:2
The correct Answer is:a
Since the ligth from slit S1 and S2 reach the point P with a path difference of λ/2, the point P will be dark, I=0. Since path difference is zero for R, there will be a bright fringe at R. So, ratio of intensity will be zero. So choice (a) is correct.
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Integer
Explore 3 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Archives
Explore 4 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Assertion- Reasoning
Explore 13 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:QUESTION BANK
Explore 34 Videos
- WAVESBook:CENGAGE PHYSICSChapter:WAVESExercise:QUESTION BANK
Explore 38 Videos
Similar Questions
Young's double slit experiment is conducted with light of wavelength λ.The intensity of the bright fringe is "1" .The intensity at a point where the path difference is3λ4 is given by
View SolutionIn an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View Solution
Knowledge Check
When light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
At point having a path difference of λ4, the intensityA0Ba2C2a2Da2/2When light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
If the path difference between the slits S1 and S2 is λ2 the central fringe will have an intensity ofA0Ba2C2a2D4a2In Young's double slit experiment the amplitudes of two sources are 3a and a respectively. The ratio of intensities of bright and dark fringes will be
A(a) 3:1B(b) 4:1C(c) 2:1D(d) 9:1
In an interference experiment, third bright fringe is obtained at a point on the screen with a light of 700 nm . What should be the wavelength of the light source in order to obtain 5th bright fringe at the same point
View SolutionInterference fringes are obtained due to the interference of wave from two coherent sources of light with amplitudes a1 and a2(a1=2a2). The ratio of the maximum and minimum intensities of light in the interference pattern is
View SolutionIn a standard YDSE slit width is 1mm and distance of screen from the slit is 1m. If wavelength of light is 632nm and bright fringe formed at y = 1.270 mm. Find path difference for the point
View SolutionThe ratio of the intensity at the centre of a bright fringe to the intensity at a point one-quarter of the distance between two fringe from the centre is
View SolutionThe ratio of the intensity at the centre of a bright fringe to the intensity at a point one quarter of the fringe width from the centre is
View Solution

