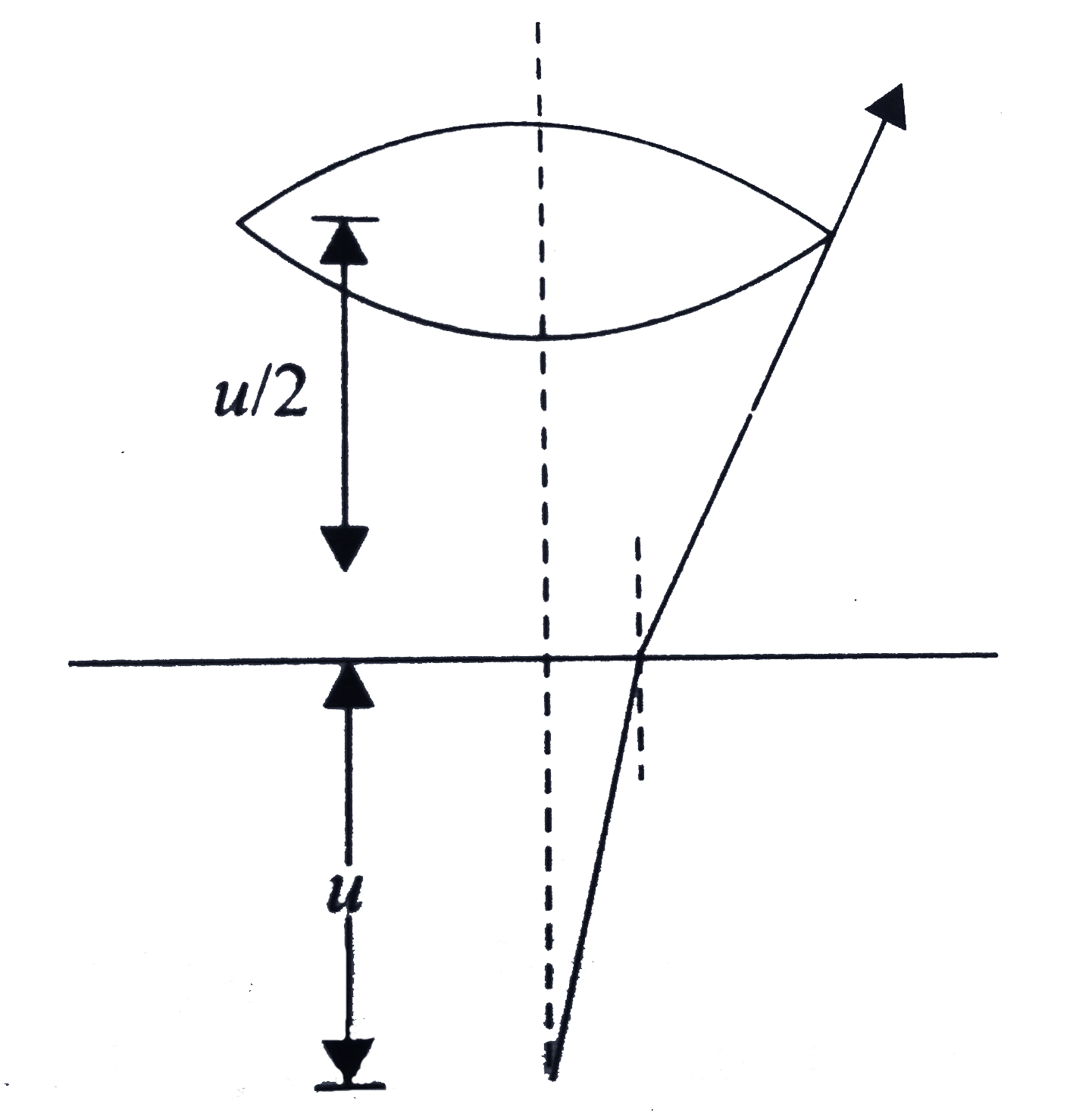
A fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
4
6
7.5
9
The correct Answer is:c.
For a plane water surface,
1v−4/3(−u)=1−4/3∞=0
or v=−0.75u
For convex lens.
μ1=1,μ2=1,
u1=−(0.75+0.5)u
=−1.25u
v1=−(u+0.5u)=−1.5u
Rays are coming from air and are viewed through air.
From 1v1−1u1=1f⇒−11.5u−1(−1.25u)=1f
or f=7.5u
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A convex lens forms a real image of pencil at a distance of 50 cm from the lens . The image formed is of the same size as the object . Find the focal length and power of the lens. At what distance is the pencil placed from the lens ?
View SolutionA convex lens forms a real and inverted image of a pencial at a distance of 60 cm from the lens. The image formed is of the same size as the object. Find the focal length and power of the lens. At what distance is the pencil placed from the lens. ?
View Solution
Knowledge Check
A fish in water (refractive index n ) looks at a bird vertically above in the air. If y is the height of the bird and x is the depth of the fish from the surface, then the distance of the bird as estimated by the fish is
Ax+y(1+1n)By+x(1−1n)Cy+x(1−1n)Dx+y(1−1n)An equi-convex glass lens with radius of each face as R is placed in air (.aug=3/2). "If there is water in the object space and air in the image space and given" .auw=4/3, the focal length of the lens is
A4 RB2 RC3R2DRIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
A5.5 mB6 mC83mD203m
Find the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionA convex lens forms a real and inverted image of a pencil at a distance of 40 cm from the lens. The image formed is of the same size as the object Find the focal length and power of the lens. At what distance is the : object placed from the lens?
View SolutionA bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionA convex lens of focal length f produces an image 1/n times the size of the object. The distance of the object from the lens is
View Solution
