Question

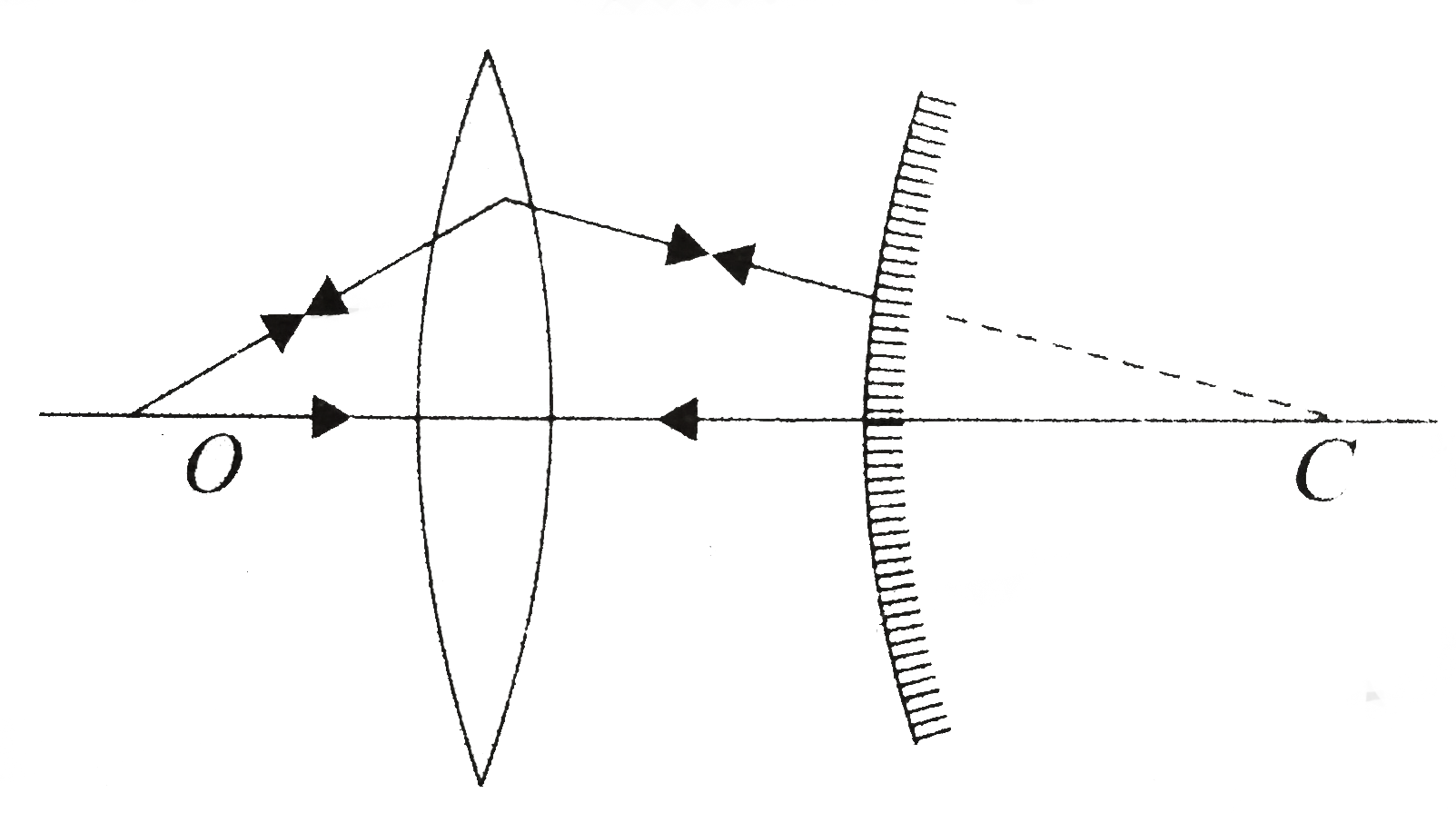
A point object is placed at a distance of ${\displaystyle 12cm}$ from a convex lens of focal length ${\displaystyle 10cm.}$ On the other side of the lens, a convex mirror is placed at a distance of ${\displaystyle 10cm}$ from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is

Options

A. `20 cm`
B. `25 cm`
C. `15 cm`
D. `30 cm`

Answer

B

Explanation

To solve the problem step by step, we need to determine the focal length of the convex mirror based on the information provided about the convex lens and the distances involved.

1. Identify the Given Information:
- Object distance from the convex lens (u) = -12 cm (negative because it is on the same side as the incoming light).
- Focal length of the convex lens (f) = +10 cm (positive for a convex lens).
- Distance from the lens to the convex mirror = 10 cm.

2. Use the Lens Formula:
The lens formula is given by:
\( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \)
Rearranging this to find v (the image distance):
\( \frac{1}{v} = \frac{1}{f} + \frac{1}{u} \)

3. Substitute the Values:
Substitute \( f = 10 \) cm and \( u = -12 \) cm into the equation:
\( \frac{1}{v} = \frac{1}{10} + \frac{1}{-12} \)
Finding a common denominator (60):
\( \frac{1}{v} = \frac{6}{60} - \frac{5}{60} = \frac{1}{60} \)

4. Calculate v:
\( v = 60 \text{ cm} \)
This means the image formed by the lens is located 60 cm on the opposite side of the lens.

5. Determine the Radius of Curvature (r) for the Convex Mirror:
Since the convex mirror is placed 10 cm from the lens, the distance from the image formed by the lens to the mirror is:
\( r = v - 10 \text{ cm} = 60 \text{ cm} - 10 \text{ cm} = 50 \text{ cm} \)

6. Calculate the Focal Length of the Convex Mirror:
The focal length (F) of a mirror is related to its radius of curvature (r) by the formula:
\( F = \frac{r}{2} \)
Therefore,
\( F = \frac{50 \text{ cm}}{2} = 25 \text{ cm} \)

Final Answer:
The focal length of the convex mirror is 25 cm.