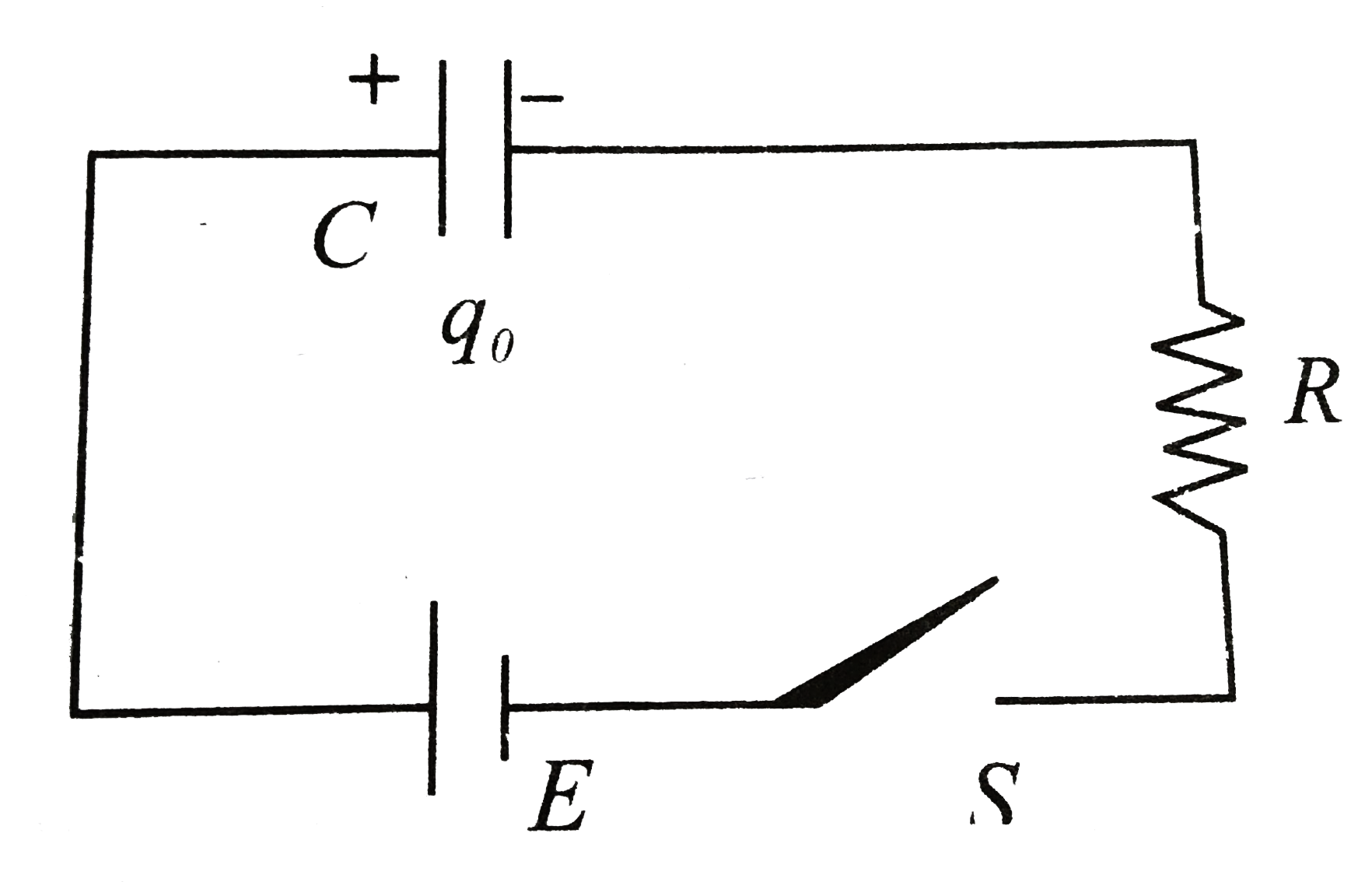
A capacitor having initial charge q0=CE/2 is connected to a cell of emf E through a resistor R as shown. Find the total heat generated in the circuit after the switch S is closed.
(1/12)CE2
(1/8)CE2
(1/4)CE2
none of these
The correct Answer is:B
b. Final charge on capacitor qf=CE
Charge flown =CE−CE/2=CE/2
Work done by battery: Wb=E(CE/2)=12CE2
Change in energy of capacitor is
ΔU=12C[q2f−q20]
=12C[(CE)2−(CE/2)2]=3CE28
Heat =Wb−ΔU=18CE2 .
Similar Questions
Knowledge Check
In the circuit shown in the figure, the capacitor C is charged to a potential Vo. The heat generated in the circuit when the switch S is closed, is
ACV20B2CV20C4CV20D8CV20A 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
A10B20C100D200Find heat produced in the capacitors after long time on closing the switch S
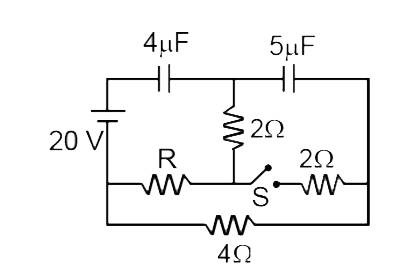 A0.0002JB.0005JC0.00075JDzero
A0.0002JB.0005JC0.00075JDzero
A capacitor C(=100μF) is charged with a total charge of 1.2×10−3C and connected in a circuit as shown. Find the current in the circuit after the key k is closed ( t= 0) as a function of time (t). Notice that the positively charged plate of the capacitor is connected to the negative terminal of the cell

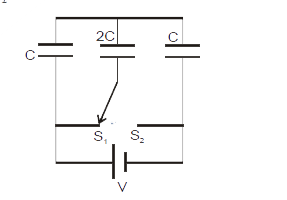
View SolutionIn the circuit shown, each capacitor has a capacitance C, The cell voltage is E, Find the amount of charge flowing through the switch when it is closed and also find the heat dissipated in the circuit when the switch is closed.
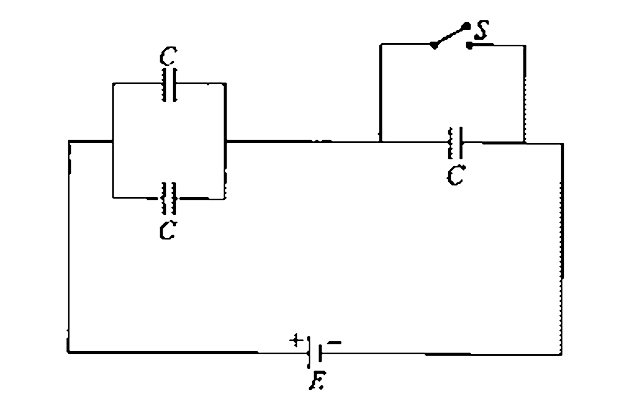
View SolutionFind the charge flown through the path 1, 2, 3 as shown in figure after closing switch S and heat generated in the circuit.

View SolutionFind the charge flown through the path 1, 2, 3 as shown in figure after closing switch S and heat generated in the circuit.

View SolutionIn the circuit shown, a capacitor charged to a potential difference V0 is connected to an uncharged capacitor through a resistor at t=0, by closing the switch. Find current in the circuit as function of time.
 .
.
View Solution