Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Charge q is
−8μC
−6.5μC
−5μC
+6.5μC
The correct Answer is:C
To solve the problem, we need to determine the charge q that is held at the point (0, 0.1 m) on the y-axis, given the forces acting on it due to two fixed point charges Q.
1. Identify the Charges and Their Positions:
- We have two equal point charges, each Q=8μC=8×10−6C, located at points (2m,0) and (−2m,0).
- The charge q is held at the point (0,0.1m).
2. Calculate the Distance from Charge Q to Charge q:
- The distance from either charge Q to charge q can be calculated using the distance formula:
r=√(2−0)2+(0−0.1)2=√4+0.01=√4.01m
3. Calculate the Force on Charge q:
- The force F experienced by charge q due to one charge Q is given by Coulomb's Law:
F=k|Q⋅q|r2
- Here, k=9×109N⋅m2/C2 and r2=4.01.
4. Calculate the Components of the Force:
- Since there are two charges Q, the total force Ftotal acting on charge q will have components from both charges.
- The horizontal components will cancel out, and only the vertical components will add up:
Ftotal=2Fcos(θ)
- Where cos(θ)=0.1√4.01.
5. Substituting the Values:
- We know that at t=0, the force experienced by q is 9×10−3N:
9×10−3=2⋅k|Q⋅q|(4.01)⋅0.1√4.01
6. Rearranging to Solve for q:
- Rearranging the equation gives:
q=9×10−3⋅4.01⋅√4.012⋅k⋅Q⋅0.1
7. Substituting Values:
- Substitute k=9×109N⋅m2/C2 and Q=8×10−6C:
q=9×10−3⋅4.01⋅√4.012⋅(9×109)⋅(8×10−6)⋅0.1
8. Calculating q:
- Calculate the values step by step to find q:
q≈−5μC=−5×10−6C
Final Answer:
The charge q is approximately −5μC.
- We have two equal point charges, each Q=8μC=8×10−6C, located at points (2m,0) and (−2m,0).
- The charge q is held at the point (0,0.1m).
- The distance from either charge Q to charge q can be calculated using the distance formula:
r=√(2−0)2+(0−0.1)2=√4+0.01=√4.01m
- The force F experienced by charge q due to one charge Q is given by Coulomb's Law:
F=k|Q⋅q|r2
- Here, k=9×109N⋅m2/C2 and r2=4.01.
- Since there are two charges Q, the total force Ftotal acting on charge q will have components from both charges.
- The horizontal components will cancel out, and only the vertical components will add up:
Ftotal=2Fcos(θ)
- Where cos(θ)=0.1√4.01.
- We know that at t=0, the force experienced by q is 9×10−3N:
9×10−3=2⋅k|Q⋅q|(4.01)⋅0.1√4.01
- Rearranging the equation gives:
q=9×10−3⋅4.01⋅√4.012⋅k⋅Q⋅0.1
- Substitute k=9×109N⋅m2/C2 and Q=8×10−6C:
q=9×10−3⋅4.01⋅√4.012⋅(9×109)⋅(8×10−6)⋅0.1
- Calculate the values step by step to find q:
q≈−5μC=−5×10−6C
The charge q is approximately −5μC.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Interger Answer type
Explore 20 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Fill in the blanks
Explore 10 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Assertion and Reason Type
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:CENGAGE PHYSICSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Question Bank
Explore 4 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
Similar Questions
Two point charges 8 μC and −8μC are kept at points (-2cm, 0) and (2cm, 0), respectively. Calculate the electric potential at points (0, 7cm) and (4cm, 0).
View SolutionTwo point charges of, 1 μC and -1 μC are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View Solution
Knowledge Check
Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Frequency of oscillation isA8B10C5D2Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Amplitude of motion isA10cmB20cmC30cmD40cmConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Equation of SHM (displacement from mean position) can be expressed asAy=0.1sin(10πt)By=0.1sin(10πt+π/2)Cy=0.1sin(5πt+π/2)Dy=0.2sin(5πt)
two point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
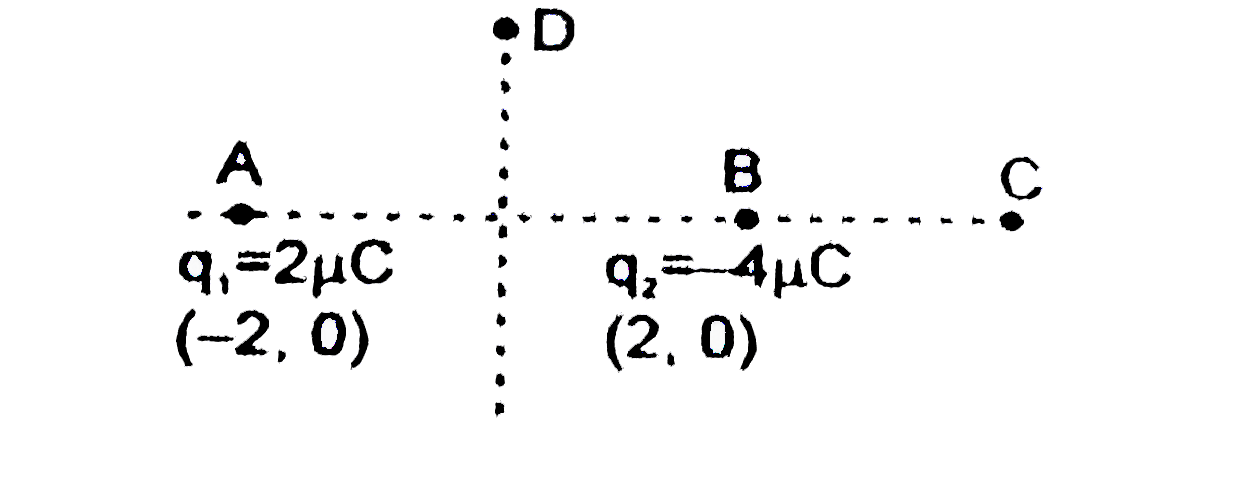
View SolutionTwo equal positive charges Q are fixed at points (a, 0) and (−a,0) on the x-axis. An opposite charge -q at rest is relased from point (0, a) on the y-axis. The charge -q will
View SolutionTwo equal negative charges −q are fixed at points (0,−a) and (0,a) on y-axis. A poistive charge Q is released from rest at point (2a,0) on the x-axis. The charge Q will
View SolutionTwo equal negative charges are fixed at points and on y-axis. A positive charge Q is released from rest at the point on the x-axis. The charge Q will:
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View Solution

