We know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Will the particle perform a simple harmonic motion? Also, find the time period of its oscillations.
Yes, time period =2πs.
No, time period =2πs
Yes, time period =4πs.
The particle will perform SHM, but time period cannot be found from the given data.
The correct Answer is:A
F=−10−5x
ma=−10−5x or 10×10−6a=−10−5x
or a=−x
ω2=1,ω=1rad.T=2πω=2π1=2πs
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Interger Answer type
20 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Knowledge Check
We know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.A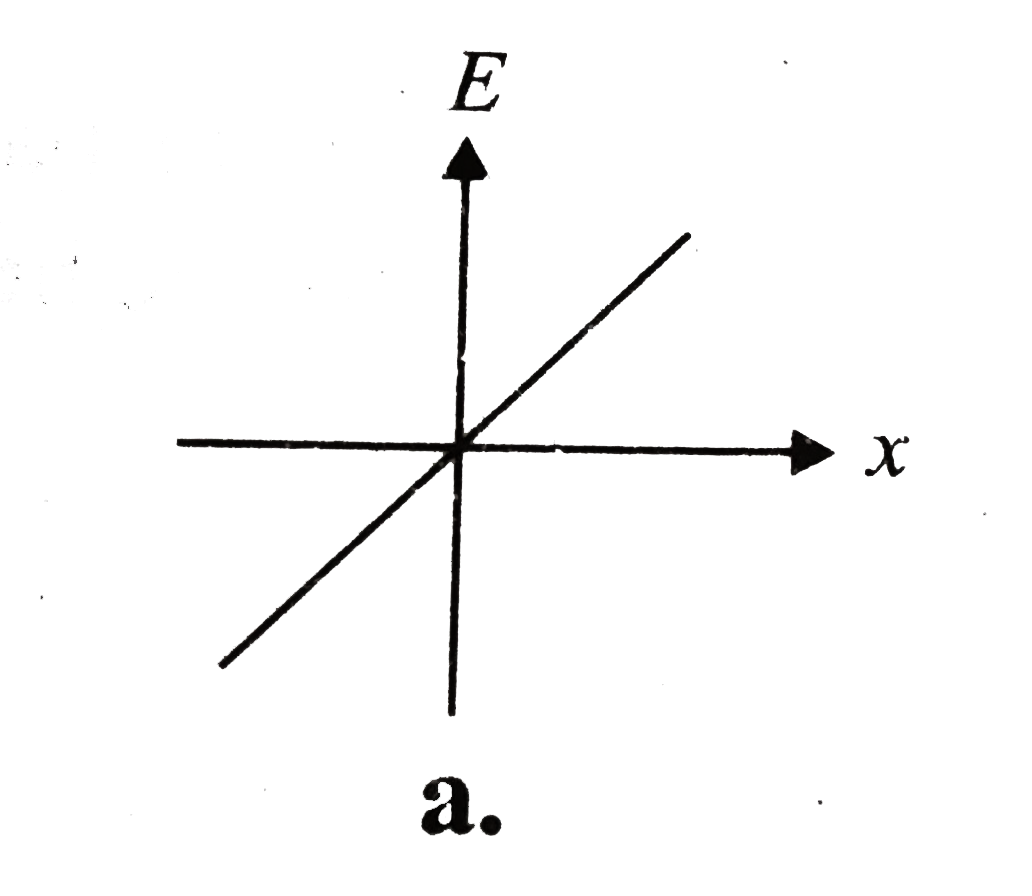 B
B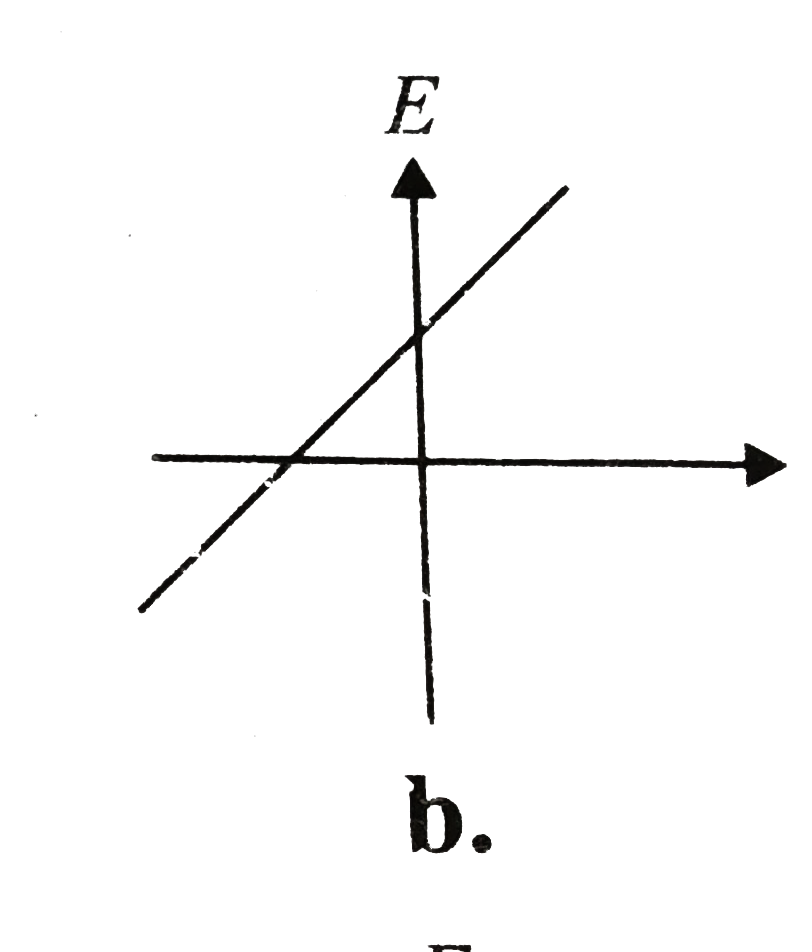 C
C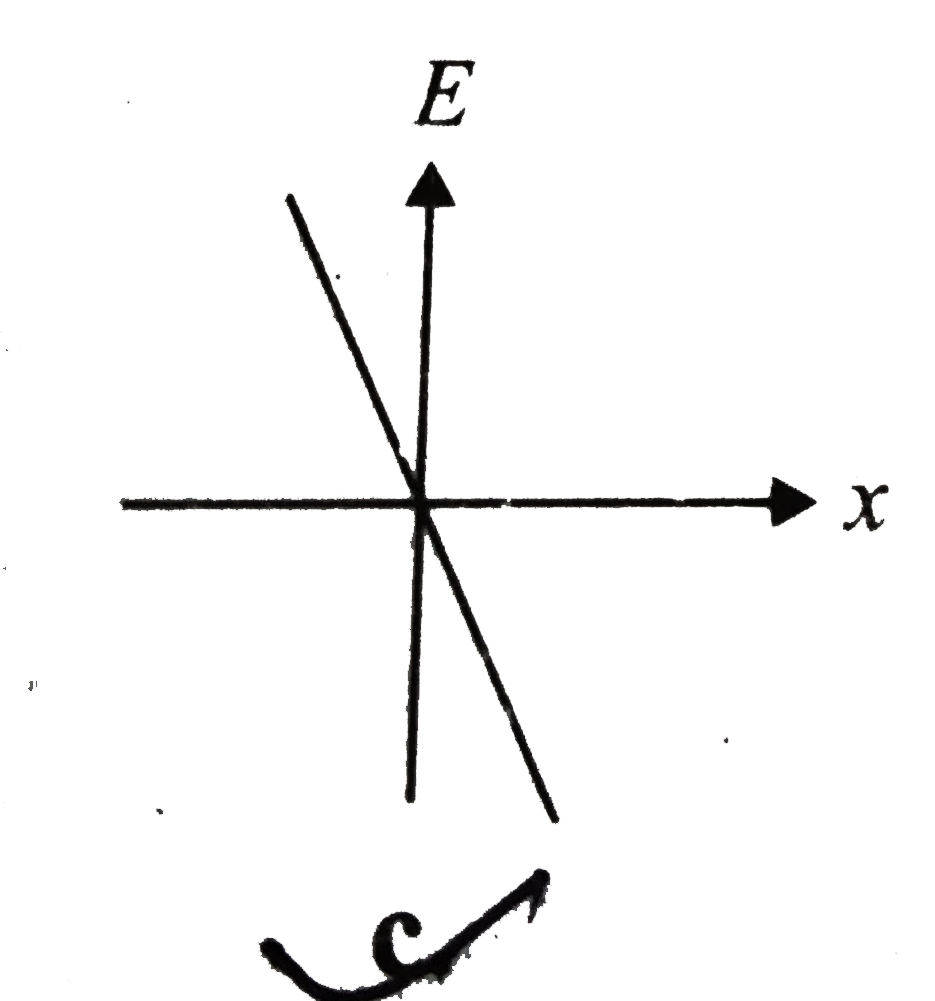 D
D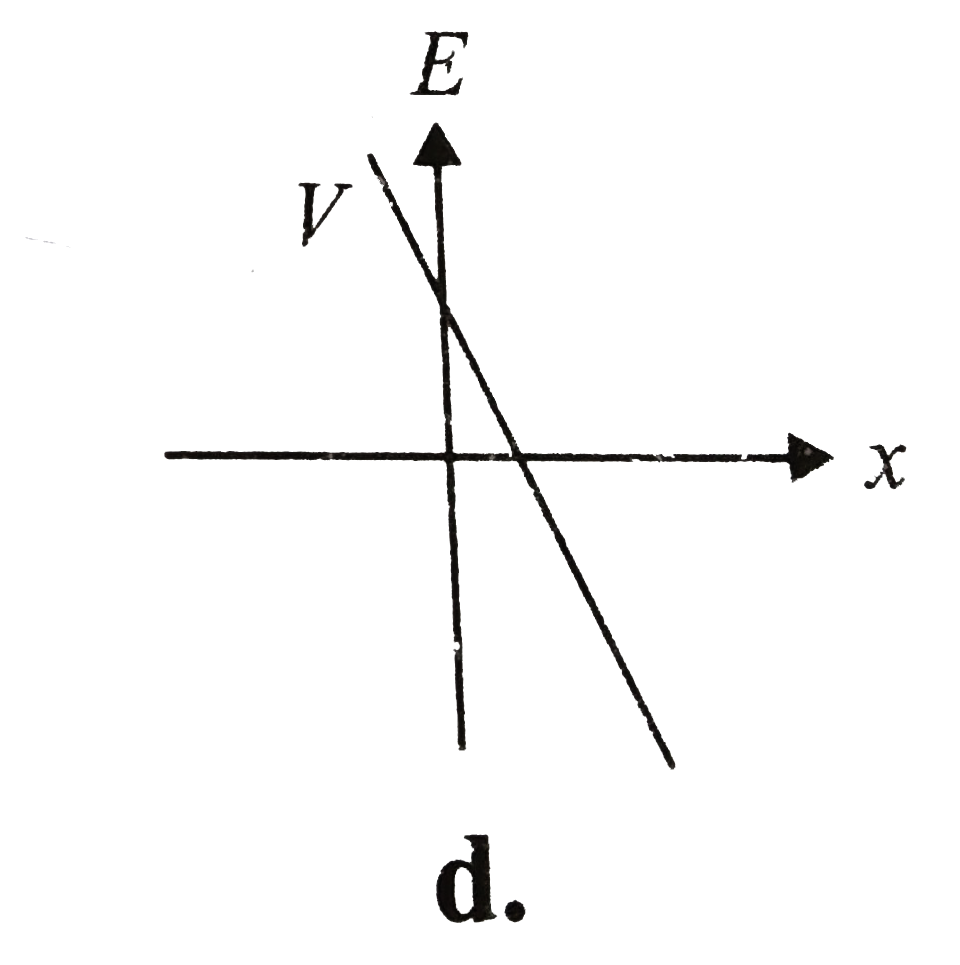
We know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
A charge particle of mass 10 mg and charge 2.5μC is released from rest at x=2m. Find its velocity when it crosses origin.A0.5ms−1B1ms−1C2ms−1D4ms−1The variation of potential with distance R from a fixed point is shown in figure. The electric field at R = 5 m is -
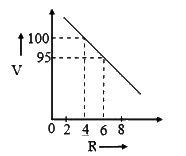 A2.5Vm−1B−2.5Vm−1C(2/5)Vm−1D−(2/5)Vm−1
A2.5Vm−1B−2.5Vm−1C(2/5)Vm−1D−(2/5)Vm−1
The electric potential at a point (x,y,z) is given by V=−s2
View Solutionthe electric potential in the region of space is given by :V(x)=A+Bx+Cx2 where V is in volts,x is in meters and A,B,C are constants.Then,
View SolutionLet V be the electric potential at a given point. Then the electric field Ex along x-direction at that point is given by :
View SolutionLet V be the electric potential at a given point. Then the electric field Ex along x-direction at that point is given by :
View SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
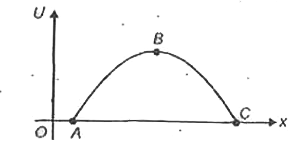
The body is in equilibrium state at
View Solution
