Two point charges 8 μC and −8μC are kept at points (-2cm, 0) and (2cm, 0), respectively. Calculate the electric potential at points (0, 7cm) and (4cm, 0).
To solve the problem of calculating the electric potential at the specified points due to the two point charges, we will follow these steps:
Given Data:
- Charge q1=8μC=8×10−6C at point (−2cm,0)
- Charge q2=−8μC=−8×10−6C at point (2cm,0)
- Point A: (0,7cm)
- Point B: (4cm,0)
Step 1: Calculate the electric potential at point A (0, 7 cm)
1. Distance from q1 to point A:
r1=√(0−(−2))2+(7−0)2=√(2)2+(7)2=√4+49=√53cm
2. Distance from q2 to point A:
r2=√(0−2)2+(7−0)2=√(−2)2+(7)2=√4+49=√53cm
3. Calculate the potentials due to each charge:
V1=k⋅q1r1=9×109⋅8×10−6√53×10−2=72×103√53V
V2=k⋅q2r2=9×109⋅(−8×10−6)√53×10−2=−72×103√53V
4. Total potential at point A:
VA=V1+V2=72×103√53−72×103√53=0V
Step 2: Calculate the electric potential at point B (4 cm, 0)
1. Distance from q1 to point B:
r1=√(4−(−2))2+(0−0)2=√(6)2=6cm
2. Distance from q2 to point B:
r2=√(4−2)2+(0−0)2=√(2)2=2cm
3. Calculate the potentials due to each charge:
V1=k⋅q1r1=9×109⋅8×10−66×10−2=72×1036=12×103V
V2=k⋅q2r2=9×109⋅(−8×10−6)2×10−2=−72×1032=−36×103V
4. Total potential at point B:
VB=V1+V2=12×103−36×103=−24×103V
Final Answers:
- Electric potential at point A (0, 7 cm): VA=0V
- Electric potential at point B (4, 0): VB=−24×103V
- Charge q1=8μC=8×10−6C at point (−2cm,0)
- Charge q2=−8μC=−8×10−6C at point (2cm,0)
- Point A: (0,7cm)
- Point B: (4cm,0)
r1=√(0−(−2))2+(7−0)2=√(2)2+(7)2=√4+49=√53cm
r2=√(0−2)2+(7−0)2=√(−2)2+(7)2=√4+49=√53cm
V1=k⋅q1r1=9×109⋅8×10−6√53×10−2=72×103√53V
V2=k⋅q2r2=9×109⋅(−8×10−6)√53×10−2=−72×103√53V
VA=V1+V2=72×103√53−72×103√53=0V
r1=√(4−(−2))2+(0−0)2=√(6)2=6cm
r2=√(4−2)2+(0−0)2=√(2)2=2cm
V1=k⋅q1r1=9×109⋅8×10−66×10−2=72×1036=12×103V
V2=k⋅q2r2=9×109⋅(−8×10−6)2×10−2=−72×1032=−36×103V
VB=V1+V2=12×103−36×103=−24×103V
- Electric potential at point A (0, 7 cm): VA=0V
- Electric potential at point B (4, 0): VB=−24×103V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 3
Explore 3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 4
Explore 7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 1
Explore 10 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Two point charges of magnitude 4 μC and-4μC are kept at points (-2 cm, 0) and (2 cm, 0) respectively. Calculate the magnitude of electric field intensity at points (0, 2 cm).
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).

View Solution
Knowledge Check
Three point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at the origin.
A2.0×103VB9.0×103VC1.0×103VD10×103VThree point charges 1μC,1μC and −2μC are placed at points having coordinates (0,1,0)cm, (1,0,0) cm and (0,0,0)cm respectively. The magnitude of electric dipole moment of the system is
A10−8CmB√2×10−8CmC√3×10−8CmD2×10−8Cm
Two identical charges of -0.1 μC are palced at point A (0, 0) and B (8cm, 0) respectively. Calculate the value of charge Q to be placed at a point M (4 cm, 0) such that the electrostatic potential energy of the system is zero.
View SolutionPoint charges q1=4 μC and q2 = -2 μC are kept at point x = 0 and x = 4 respectively , electrical potential will be zero at points (where x is in cm)
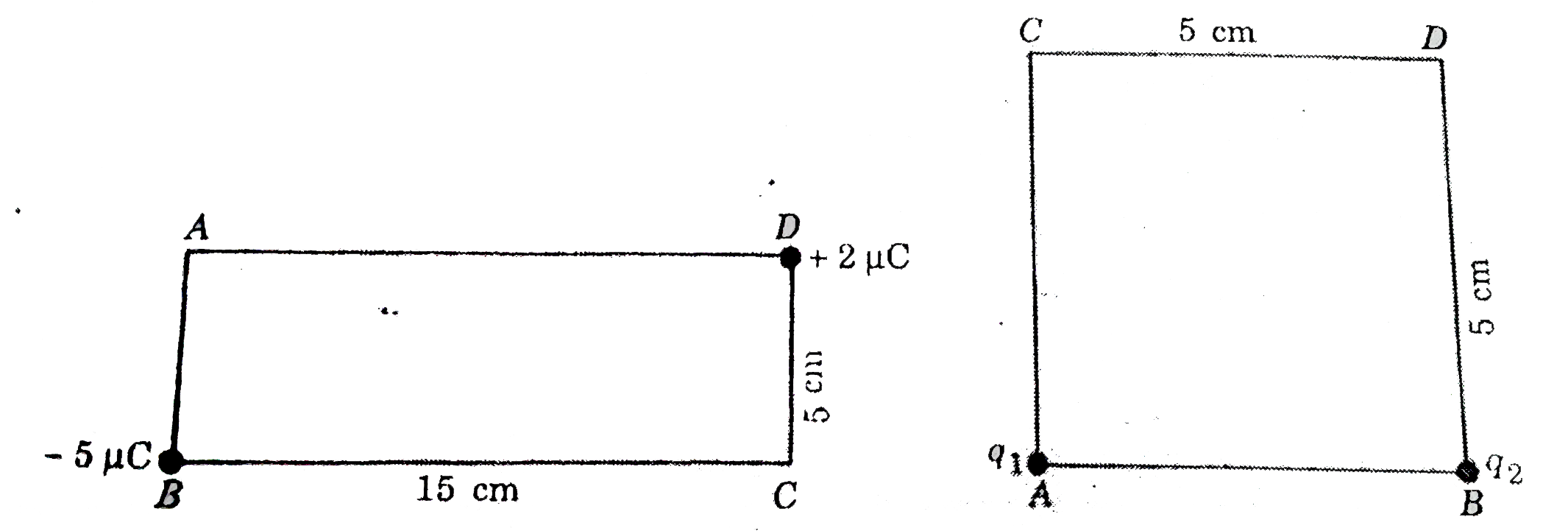
View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
View SolutionThe point charges q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at origin.
View SolutionTwo identical charges of 1μC are kept on 0,2 m) and (0,-2 m), respectively. Calculate the magnitude of the force acting on a 2μC charge placed at (-5m,0).
View SolutionTwo point charges 10μCand−10μC are separated by a distance of 40 cm in air.
Calculate the electrostatic potential energy of the system, assuming the zero of the potential energy to be at infinity.
View Solution

