A charged particle of mass m = 2 kg and charge 1μC is projected from a horizontal ground at an angle θ=45∘ with speed 10ms−1. In space, a horizontal electric field towards the direction of projection E=2×107NC−1 exists. The range of the projectile is
20 m
60 m
200 m
180 m
The correct Answer is:A
ax=qEm=10−4×2×1072=10ms−2
Tune of flight =2usinθg=2×10×1√210=√2s
Hence R=uxT+12axT2
=10cos45∘×T+12axT2
=10√2×√2+12×10×2
=20m.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type109videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank4videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A charged particle of mass m=1 kg and charge q=2μC is thrown from a horizontal ground at an angle θ=45∘ with the speed 25m/s. In space, a horizontal electric field E=2×107 V/m exists in the direction of motion. Find the range on horizontal ground of the projectile thrown. Take g=10m/s2.
View SolutionA charged particle of mass m=1 kg and charge q=2μC is thrown for a horizotal ground at an angle θ=45∘ with speed 20m/s. In space a horizontal electric field E=2×107 V/m exist. Find the range on horizontal ground of the projectile thrown.
View Solution
Knowledge Check
- Question 1 - Select One
A charged particle of mass m=2kg and charge 1μC is thrown from a horizontal ground at an angle of 45∘ with horizontal with a spedd of 10m/s. In space a horizontal electric field E=2×107N/C exists. Find the range of the projectile
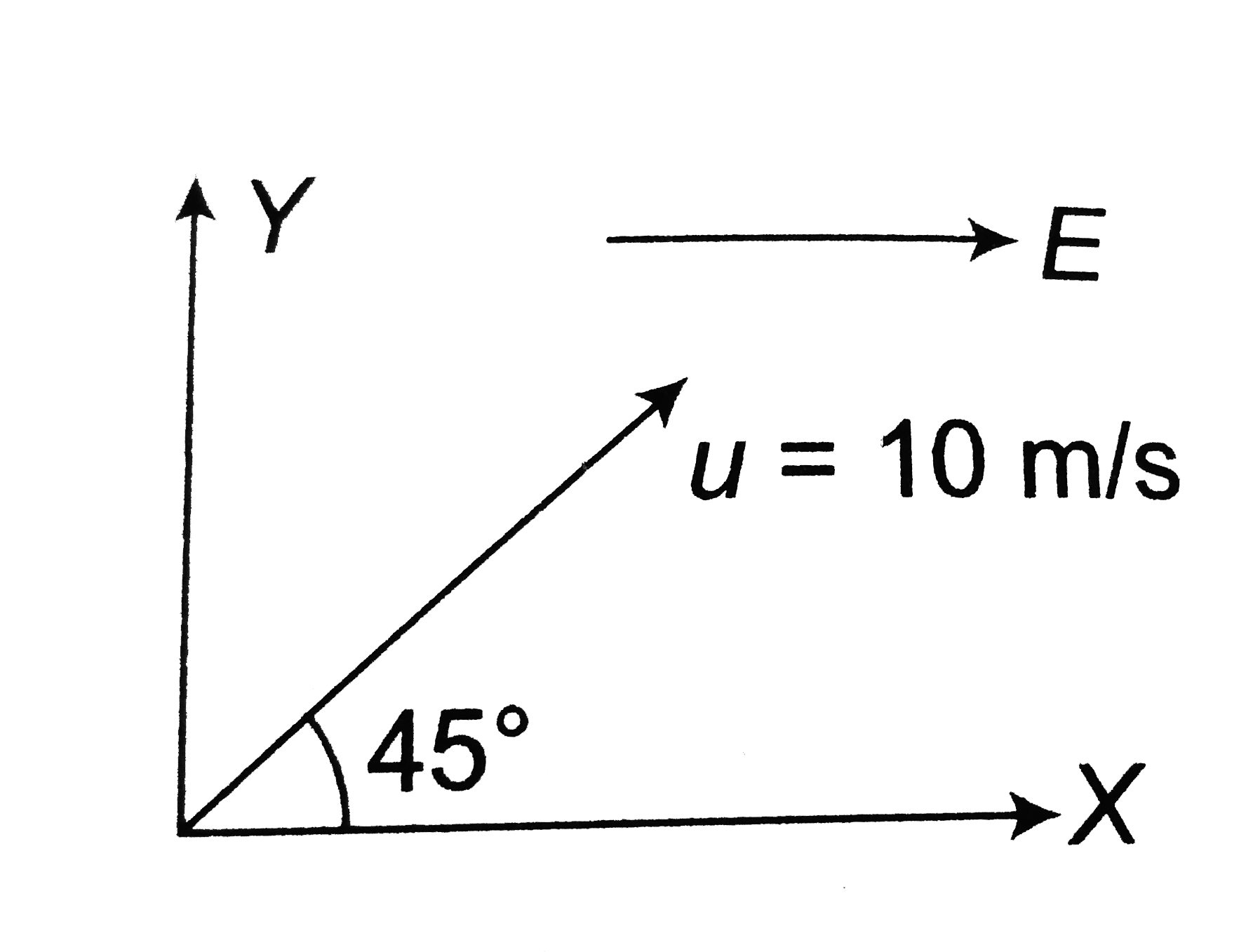A5mB30mC10mD20m - Question 2 - Select One
A particle is projected from horizontal ground at angle 'θ' with speed 'u'. In same plane of motion a horizontal acceleration 'a' exists so that projected particle returns back to point of projection. Find time of flight.
A2usinθgB3usinθgC2ucosθαD3ucosθα - Question 3 - Select One
A particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
AThe kinetic energy after a displacement y is qEyBThe horizontal and vertical components of acceleration of ax=0,ay=qEmCthe equation of trajectory is y=12(qEx2mv2)DThe horizontall and verticasl displacements x and y after a time t x=vt and y=12ayt2
A particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA particle of mass m and charge q is thrown with initial velocity v0 at an angle with the horizontal. In space there exist an electric field of strength E at angle β with the downward vertical away from the point of projection. Find the time of flight and range of projectile on horizontal ground
View SolutionA particle is projected from horizontal ground with speed 5ms−1 at 53∘ with horizontal. Find time after which velocity of particle will be 45∘ with horizontal:
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
View SolutionA particle is projected from horizontal making an angle of 53∘ with initial velocity 100ms−1. The time taken by the particle to make angle 45∘ from horizontal is
View Solution