From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
10√3
20 m
20√3m
40√3
The correct Answer is:C
To find the horizontal range of a projectile fired at an angle, we can use the formula:
R=u2sin(2θ)g
Where:
- R is the horizontal range,
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 10m/s2).
Step 1: Identify the given values
- Initial speed u=20m/s
- Angle of projection θ=60∘
- Acceleration due to gravity g=10m/s2
Step 2: Calculate sin(2θ)
Using the angle θ=60∘:
2θ=120∘
Now, we need to find sin(120∘):
sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
Step 3: Substitute the values into the range formula
Now substituting the values into the range formula:
R=(20m/s)2⋅sin(120∘)10m/s2
R=400⋅√3210
Step 4: Simplify the expression
R=400⋅√3210=400√320=20√3m
Final Answer
The horizontal range of the projectile is:
R=20√3m
- R is the horizontal range,
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 10m/s2).
- Initial speed u=20m/s
- Angle of projection θ=60∘
- Acceleration due to gravity g=10m/s2
Using the angle θ=60∘:
2θ=120∘
Now, we need to find sin(120∘):
sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
Now substituting the values into the range formula:
R=(20m/s)2⋅sin(120∘)10m/s2
R=400⋅√3210
R=400⋅√3210=400√320=20√3m
The horizontal range of the projectile is:
R=20√3m
Topper's Solved these Questions
Similar Questions
A particle is projected at an angle of60∘ above the horizontal with a speed of 10m/s .When the projectile reaches highest point, change in velocity is
View SolutionA projectile is fired at an angle of 30° to the horizontal with the speed v. If another projectile is projected with the same speed, then at what angle with the horizontal it must be projected so as to have the same range ?
View Solution
Knowledge Check
The horizontal range for projectile is given by
Au2θsin2θgBu2sin2θgCu2sin2θ2gDu2cos2θgIn case of a projectile fired at an angle equally inclined to the horizontal and vertical with velocity (u). The horizontal range is:-
Au2gBu22gC2u2gDu2g2The horizontal range covered by projectile is proportional to
Aits velocityBsquare of its velocityCsine of the angle of projectionDsquare of the sine of the angle of projection
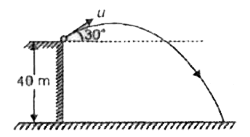
Figure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
View SolutionA projectile is fired horizontally with an initial speed of 20 m/s/ its horzontal speed 3 sec later is:
View SolutionKeeping the speed of projection constant, the angle of projection is increased from 0∘ to 90∘. Then the horizontal range of the projectile
View SolutionA particle is projected from the ground at an angle of 60∘ with horizontal at speed u=20m/s. The radius of curvature of the path of the particle, when its velocity. makes an angle of 30∘ with horizontal is :
(g=10m/s2
View SolutionA stone projected from ground with certain speed at an angle θ with horizontal attains maximum height h1 when it is projected with same speed at an angle θ with vertical attains height h2. The horizontal range of projectile is
View Solution

