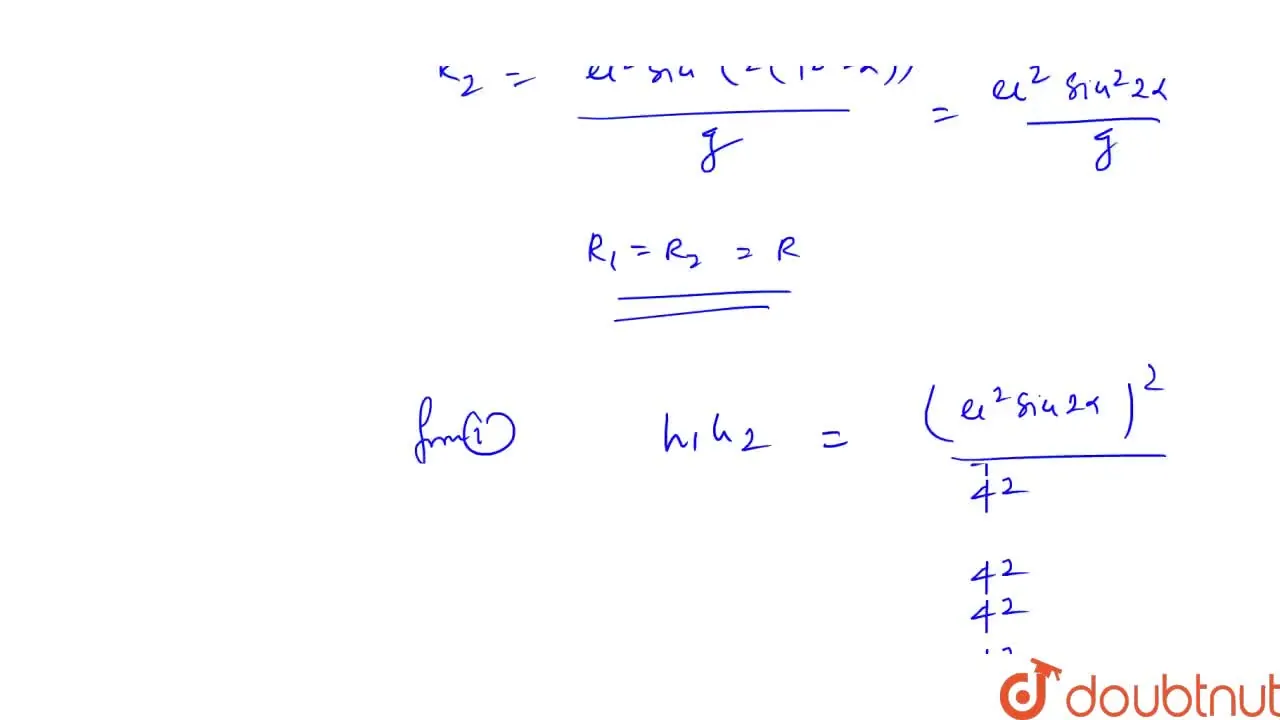A stone projected from ground with certain speed at an angle θ with horizontal attains maximum height h1 when it is projected with same speed at an angle θ with vertical attains height h2. The horizontal range of projectile is
h1+h22
2h1h2
4√h1h2
h1+h2
The correct Answer is:C
Step by step video, text & image solution for A stone projected from ground with certain speed at an angle theta with horizontal attains maximum height h_(1) when it is projected with same speed at an angle theta with vertical attains height h_(2). The horizontal range of projectile is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A stone projected with a velocity u at an angle (theta )with the horizontal reaches maximum heights H1. When it is projected with velocity u at an angle (π2−θ) with the horizontal, it reaches maximum height H2. The relations between the horizontal range R of the projectile, H1andH2, is
View SolutionA stone projected with a velocity u at an angle q with the horizontal reaches maximum heights H1. When it is projected with velocity u at an angle (π2−θ) with the horizontal, it reaches maximum height H2. The relations between the horizontal range R of the projectile, H1andH2, is
View SolutionA projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
View SolutionIf R and H are the horizontal range and maximum height attained by a projectile , than its speed of prjection is
View SolutionThe maximum height attained by a projectile when thrown at an angle θ with the horizontal is found to be half the horizontal range. Then θ is equal to
View SolutionThe maximum height attained by a projectile when thrown at an angle θ with the horizontal is found to be half the horizontal range. Then θ is equal to
View SolutionThe maximum height attained by a projectile when thrown at an angle θ with the horizontal is found to be half the horizontal range. Then θ is equal to
View SolutionParticle A is projected with speed u at an angle θ with the horizontal . Another particle B is also projected with same speed u at an angle 90−θ with the horizontal . Both the projectiles are fired from the ground and reaches the ground after completing the projectile . Time of flight for A is tA and that for B it is tB. Range of the projectile A is RA and that for B is RB . Maximum height reached by the projectile A is hA and that for B is hB
 View Solution
View SolutionThe angle of projection at which the horizontal range and maximum height of projectile are equal is
View SolutionFind the average velocilty of a projectile between the instants it crosses half the maximum height. It is projected with speed u ast angle θ with the horizontal.
View Solution