A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω resistance, the ammeter reading is 0.04A. Find the voltage reading by the voltmeter and its resistance. Had the voltmeter been an ideal one what would have been its reading?
400Ω
200Ω
300Ω
500Ω
The correct Answer is:A
Let R1 and R2 be the resistances of the ammeter and the voltmeter, respectively. Let the external resistance be denoted by R and the internal resistance of battery be r. The equivalent resistance of the parallel combination of R and R2 is given by
R'=RR2R+R2
The total resistance RT of circuit then becomes
RT=R1+r+RR2R+R2
The current in the circuit is given by
I=ER1+r+RR2R+R2
This must be equal to 0.04A, the reading indicated by the ammeter.
3.42+3+100R2100+R2=0.04 or R2=400Ω
In case of an ideal voltmeter, no current flows through it. In that case, current in the circuit is
I'=3.42+3+100=3.4105=0.0324A
Potential drop across the resistance R would br 100×0.0324=3.24V.
This should be that reading indicated by an ideal voltmeter.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:Integer
Explore 8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:Assertion-Reasoning
Explore 7 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
- ELECTROMAGENTIC INDUCTIONBook:CENGAGE PHYSICSChapter:ELECTROMAGENTIC INDUCTIONExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
(a) A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance 100Ω. When a voltmeter is connected across the 100Ω resistance the ammeter reading is 0.04A. Find the voltage read by the voltmeter and its resistance. Had the voltmeter been an ideal one, what would have its reading ?
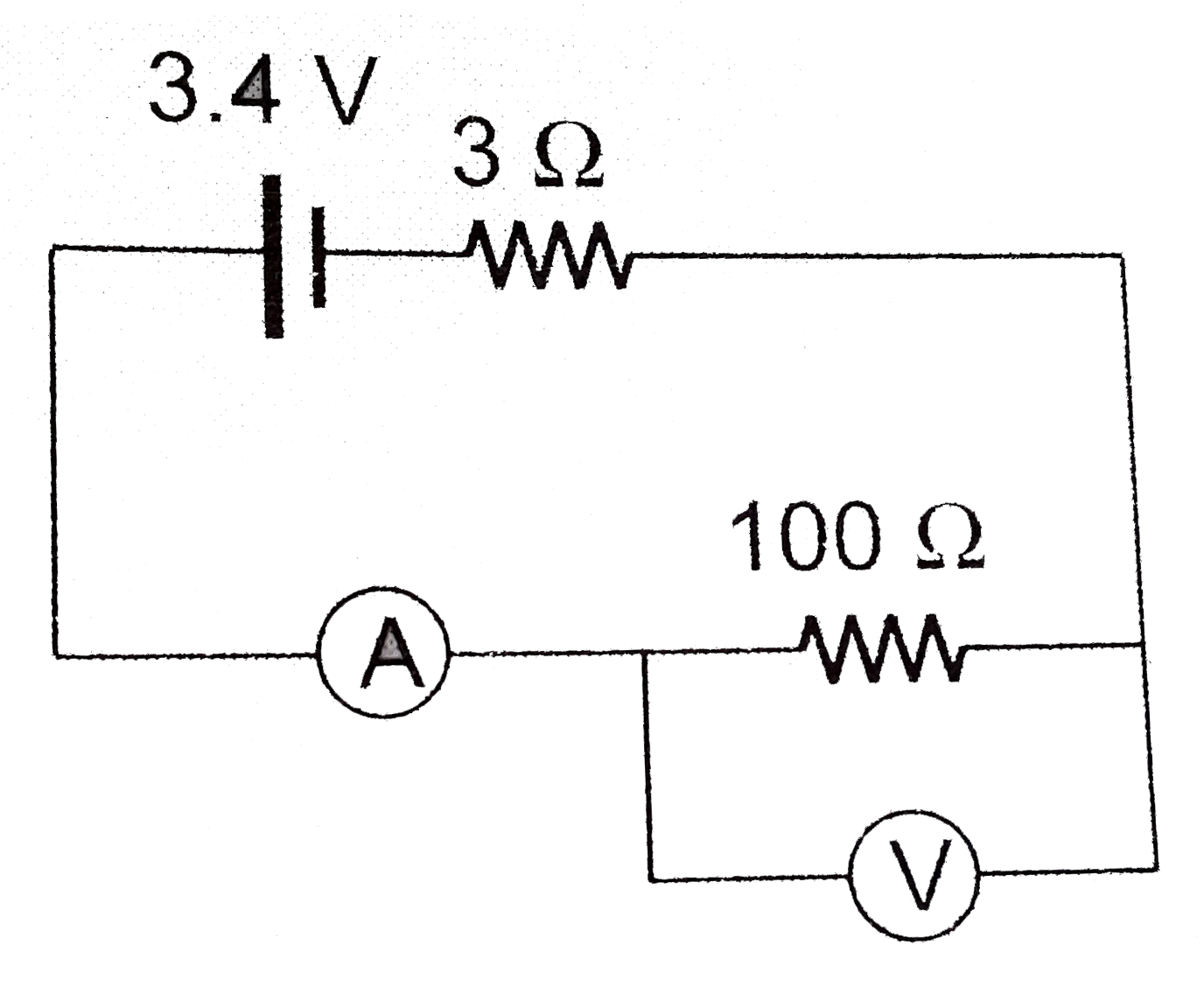
(b) Two resistances of 100Ω and 200Ω are connected in series with battery of emf 4V and negligible internal resistance. A voltmeter of resistance 200Ω is used to measure voltemeter of resistances separately. Calculate the voltmeter indicated.
( c) In the circuit shown, a voltmeter reads 30V when it is connected across the 400Ω resistance. Calculate what the same voltmeter will read when it is connected across the 300Ω resistance ?
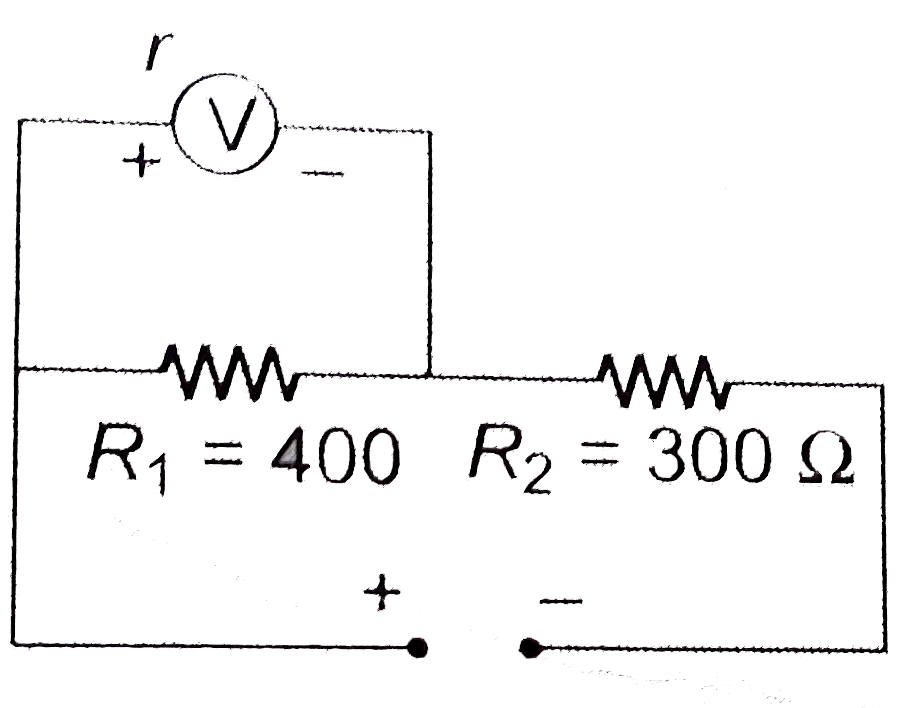
(d) An ammeter and a voltmeter are connected in series to a battery of emf E=6.0V. When a certain resistance is connected in parallel with the voltmeter. the reading of the ammeter is doubled. while voltmeter reading is reduced to half. Find the voltmeter reading after the connection of the resistance.
View SolutionA cell has an emf of 3 volt and internal resistance 2Ω. It is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω. Resistance, the ammeter reading is 40 mA. The resistance of the voltmeter is
View Solution
Knowledge Check
A voltmeter has a resistance of 50Ω is connected across a cell of e.m.f. 2V and internal resistance 10Ω. The reading of voltmeter is
A1.667VB16.7VC167VD0.167VAn ammeter is connected in series with an unknown resistance and a voltmeter is connected across the terminals of the resistance . If the ammeter reads 1.2 A and the voltmeter reads 18 V the n value of the resistance is
A21.6B18.0C15.0D9.0The voltmeter reads 40V across 60Ω resistance. The resistance of voltmeter is.
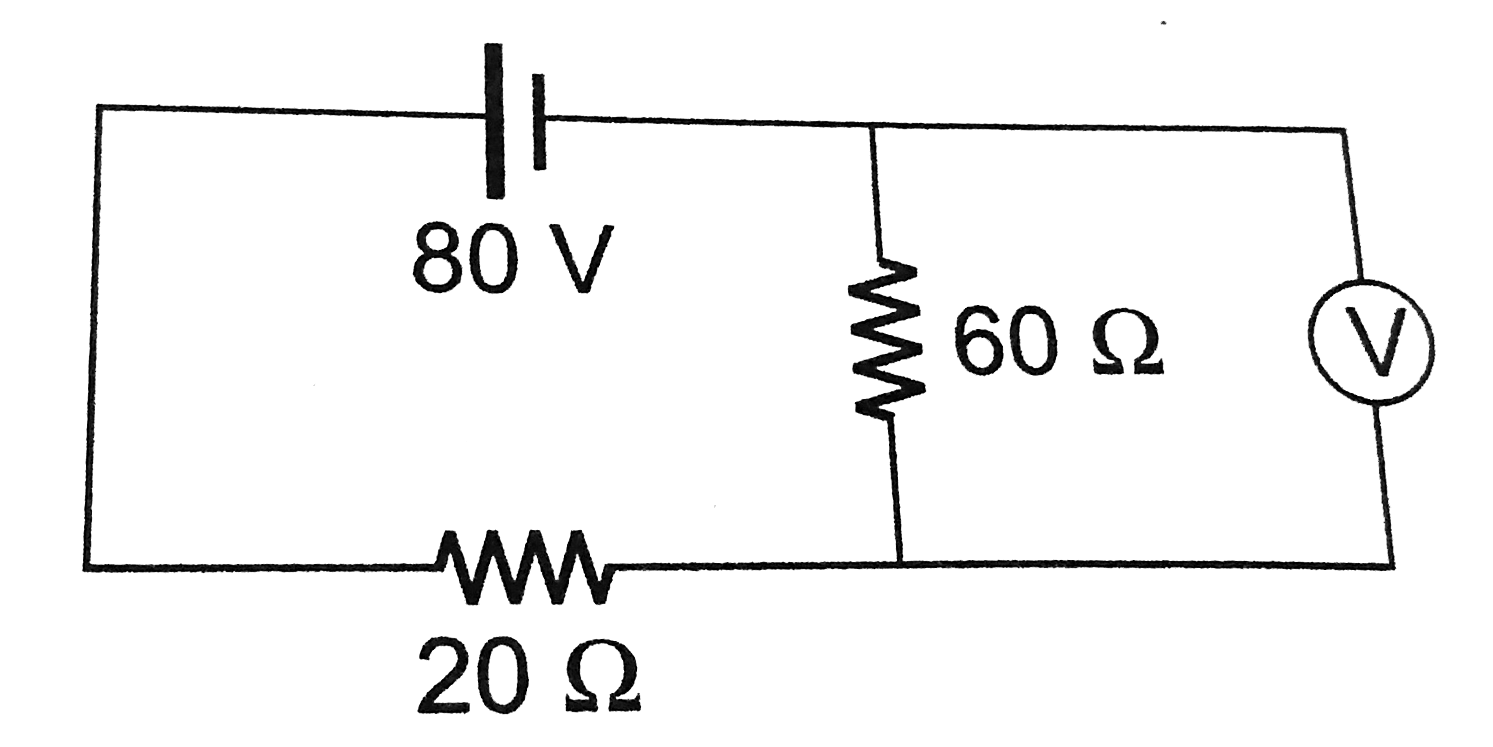 .A10ΩB20ΩC30ΩD40Ω
.A10ΩB20ΩC30ΩD40Ω
A battery of EMF 1.4 V and internal resistance 2Ω is connected to resistor of 100Ω resistance through an ammeter. The resistance of the ammeter is 43Ω. A voltmeter is also connected to find potential difference across resistor. The ammeter reacds 0.02 A if resistance of voltmeter is 100x then x is
View SolutionA battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
View SolutionA battery of emf 1.4 volt and internal resistance 2Ω is connected to a resistor is of 100Ω through an ammeter. The resistance of the ammter is 43Ω. A voltmeter has also been connected to measure the potential difference across the resistor 100Ω. If the ammeter reads 0.02A and voltmeter reading is 1.10 volt then error in the reading of voltmeter is x volt then find value of x(10025) in nearest integer.
View SolutionA battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
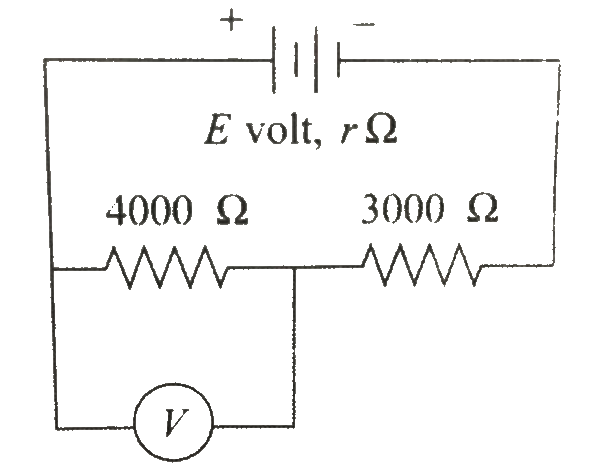
View SolutionIn Fig.6.59, when an ideal voltmetre is connected across 4000Ω resistance, it reads 30V. If the voltmeter is connected across 3000Ω resistance, it will read
View Solution

