A battery of emf 1.4 volt and internal resistance 2Ω is connected to a resistor is of 100Ω through an ammeter. The resistance of the ammter is 43Ω. A voltmeter has also been connected to measure the potential difference across the resistor 100Ω. If the ammeter reads 0.02A and voltmeter reading is 1.10 volt then error in the reading of voltmeter is x volt then find value of x(10025) in nearest integer.
The correct Answer is:1
To solve the problem, we need to analyze the circuit and calculate the error in the voltmeter reading. Here’s a step-by-step solution:
Step 1: Understand the Circuit
We have a battery with an emf of 1.4 V and an internal resistance of 2 Ω. This battery is connected to a 100 Ω resistor through an ammeter with a resistance of 43 Ω. The ammeter reads a current of 0.02 A, and we need to find the error in the voltmeter reading across the 100 Ω resistor.
Step 2: Calculate the Total Resistance in the Circuit
The total resistance Rtotal in the circuit can be calculated as:
Rtotal=Rinternal+Rammeter+Rload
Where:
- Rinternal=2Ω
- Rammeter=43Ω
- Rload=100Ω
Calculating Rtotal:
Rtotal=2+43+100=2+1.33+100=103.33Ω
Step 3: Calculate the Current Through the Circuit
The current I flowing through the circuit is given as 0.02 A. We can verify this with Ohm's law:
V=I⋅Rtotal
Calculating the voltage drop across the total resistance:
V=0.02A×103.33Ω=2.0666V
Step 4: Calculate the Voltage Across the 100 Ω Resistor
The voltage across the 100 Ω resistor can be calculated using Ohm's law:
V100=I⋅Rload=0.02A×100Ω=2V
Step 5: Calculate the Voltage Drop Across the Ammeter
The voltage drop across the ammeter can be calculated as:
Vammeter=I⋅Rammeter=0.02A×43Ω=0.02667V
Step 6: Calculate the Effective Voltage Across the Resistor
The effective voltage across the 100 Ω resistor when considering the internal resistance of the battery is:
Veffective=Vbattery−Vinternal−Vammeter
Where Vbattery=1.4V and Vinternal=I⋅Rinternal=0.02A×2Ω=0.04V:
Veffective=1.4V−0.04V−0.02667V=1.33333V
Step 7: Calculate the Error in the Voltmeter Reading
The voltmeter reads 1.10 V, but the effective voltage across the 100 Ω resistor is 1.33333 V. The error x in the voltmeter reading is:
x=Veffective−Vvoltmeter=1.33333V−1.10V=0.23333V
Step 8: Calculate x(10025)
Now, we need to find:
x(10025)=0.23333×4=0.93332
Rounding to the nearest integer gives us:
Final Answer=1
We have a battery with an emf of 1.4 V and an internal resistance of 2 Ω. This battery is connected to a 100 Ω resistor through an ammeter with a resistance of 43 Ω. The ammeter reads a current of 0.02 A, and we need to find the error in the voltmeter reading across the 100 Ω resistor.
The total resistance Rtotal in the circuit can be calculated as:
Rtotal=Rinternal+Rammeter+Rload
Where:
- Rinternal=2Ω
- Rammeter=43Ω
- Rload=100Ω
Rtotal=2+43+100=2+1.33+100=103.33Ω
The current I flowing through the circuit is given as 0.02 A. We can verify this with Ohm's law:
V=I⋅Rtotal
Calculating the voltage drop across the total resistance:
V=0.02A×103.33Ω=2.0666V
The voltage across the 100 Ω resistor can be calculated using Ohm's law:
V100=I⋅Rload=0.02A×100Ω=2V
The voltage drop across the ammeter can be calculated as:
Vammeter=I⋅Rammeter=0.02A×43Ω=0.02667V
The effective voltage across the 100 Ω resistor when considering the internal resistance of the battery is:
Veffective=Vbattery−Vinternal−Vammeter
Where Vbattery=1.4V and Vinternal=I⋅Rinternal=0.02A×2Ω=0.04V:
Veffective=1.4V−0.04V−0.02667V=1.33333V
The voltmeter reads 1.10 V, but the effective voltage across the 100 Ω resistor is 1.33333 V. The error x in the voltmeter reading is:
x=Veffective−Vvoltmeter=1.33333V−1.10V=0.23333V
Now, we need to find:
x(10025)=0.23333×4=0.93332
Rounding to the nearest integer gives us:
Final Answer=1
Topper's Solved these Questions
Similar Questions
A battery of EMF 1.4 V and internal resistance 2Ω is connected to resistor of 100Ω resistance through an ammeter. The resistance of the ammeter is 43Ω. A voltmeter is also connected to find potential difference across resistor. The ammeter reacds 0.02 A if resistance of voltmeter is 100x then x is
View SolutionA battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
View Solution
Knowledge Check
Three batteries having emfs and internal resistances as shown in figure are connected across a resistor of 2Ω. The reading of ammeter is
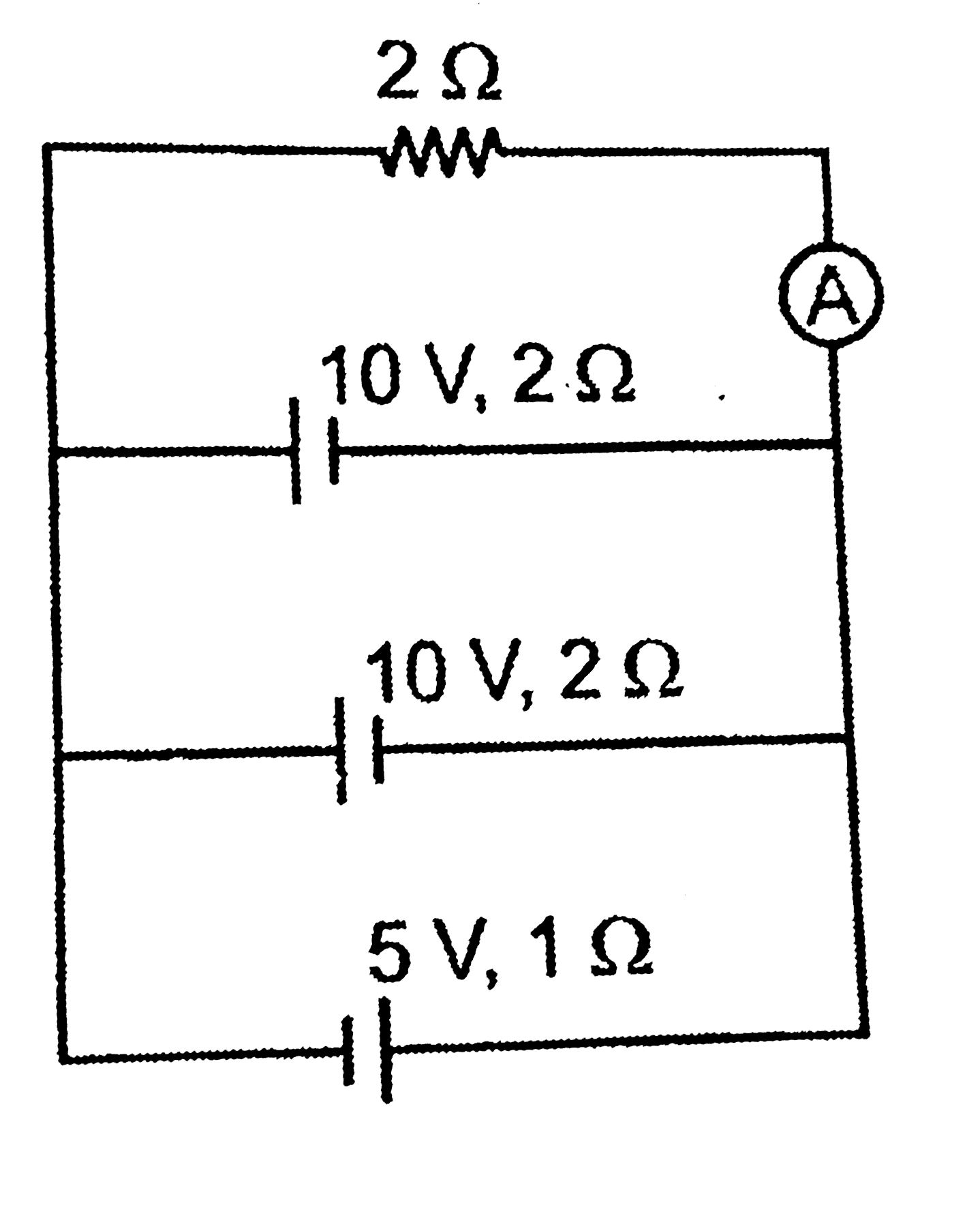 A1AB1.5AC2AD2.5A
A1AB1.5AC2AD2.5A
A battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
View SolutionA battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
View SolutionA battery of emf 3 volt and internal resistance r is connected in series with a resistor of 55Ω through an ammeter of resistance 1Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA battery of emf 3V and internal resistance r is connected in series with a resistor of 55Ω through an ammeter of resistance 1Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionThe battery of EMF 5V and internal resistance 20Ωis connected with a resistance R1=50Ω and a resistance . A voltmeter of resistance 1000Ω is used to measure the potential difference across R1 .What percentage error is made in the reading.
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
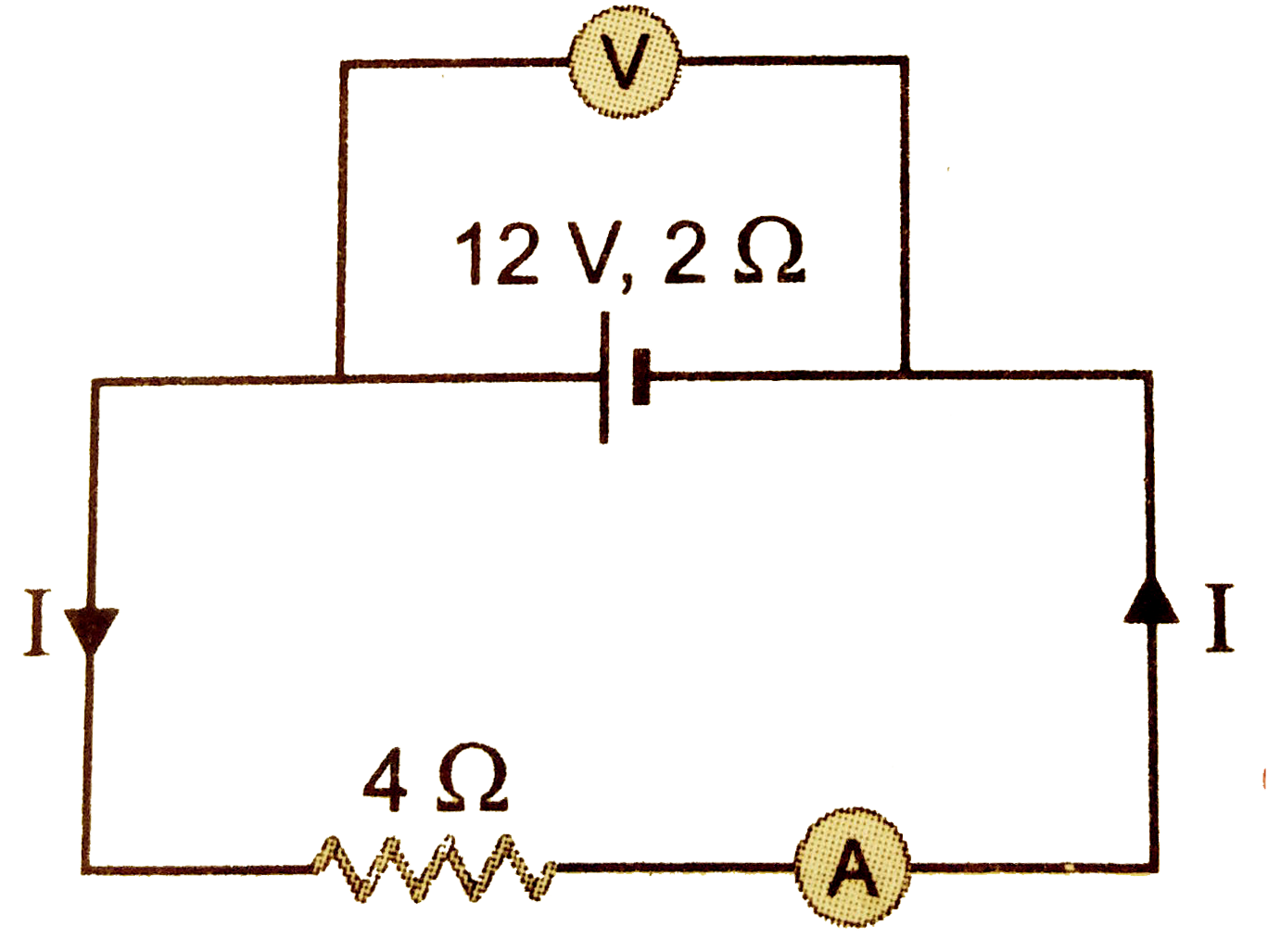
View Solution