n identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
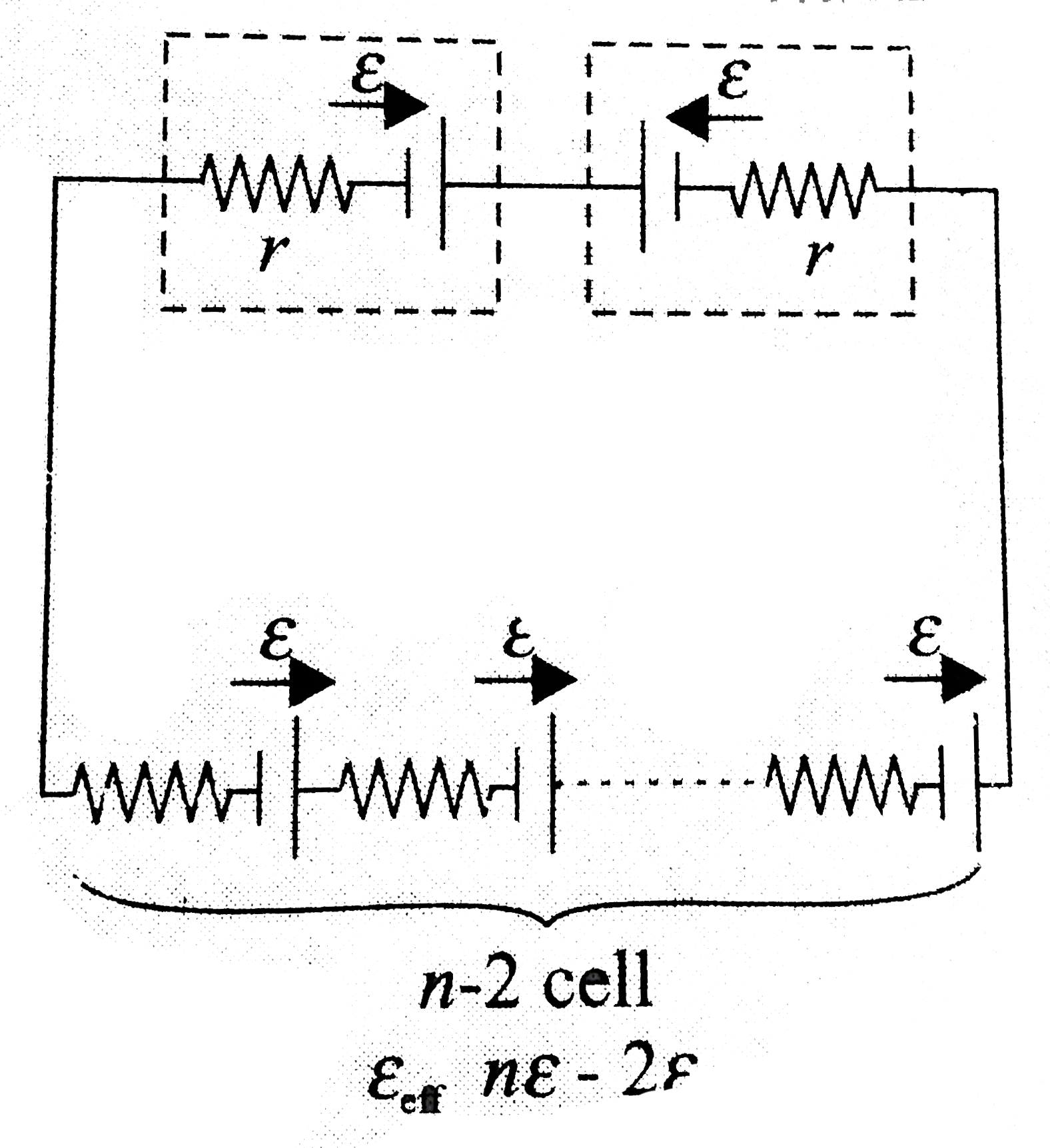
Let r be the internal resistance of each cell. For series
connection, εeff= nε=6n.
reff=nr
or I=nεnr+R=6nnr+5=10 ……(i)
For wrong connection of two cells, the effective emf decreases by 2ε because the emfs of two identical cells counteract with each other. Then,
ε'eff=nε−ε=(n−2)ε=(n−2)6
and εeff=nr
or i'=(n−2)εnr+R=(n−2)6nr+5=6.45 ......(ii)
By solving Eqs. (i) and (ii), we have n = 10 and r = 0.1Ω.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Three cells each of emf 1.5 V, after being connected in series with each other, are connected to the ends of a resistance. The current obtained is 1 A. When the cells are connected in parallel across the ends of the same resistance, the current is found to be 0.36 A. Find the external resistance and the internal resistance of each cell.
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View Solution
Knowledge Check
Two identical cells whether connected in parallel or in series gives the same current, when connected to an external resistance 1.5Ω. Find the value of internal resistance of each cell.
A1ΩB0.5ΩCZeroD1.5ΩThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
A(n−1)E(n+1)r+2B(n−1)Enr+RC(n−2)Enr+RD(n−2)E(n−2)r+Rn identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
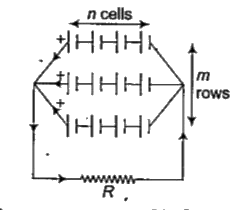 Anr=mRBnR=mrCnm=rRDnmR=r
Anr=mRBnR=mrCnm=rRDnmR=r
A cell which has an emf 1.5 V is connection series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
View SolutionA student is asked to connected four cells of emf of 1 V and internal resistance 0.5 ohm in series with an external resistance of 1 ohm. But one cells is wrongly connected by him with its terminal reversed, the current in the ciruit is
View Solutionn identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
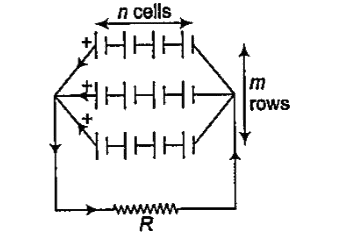
View SolutionThree similar cells, each of emf 2 V and internal resistance rΩ send the same current through an external resistance of 2Ω, when connected in series or in parallel. The strength of the current flowing through the external resistance is
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solution

