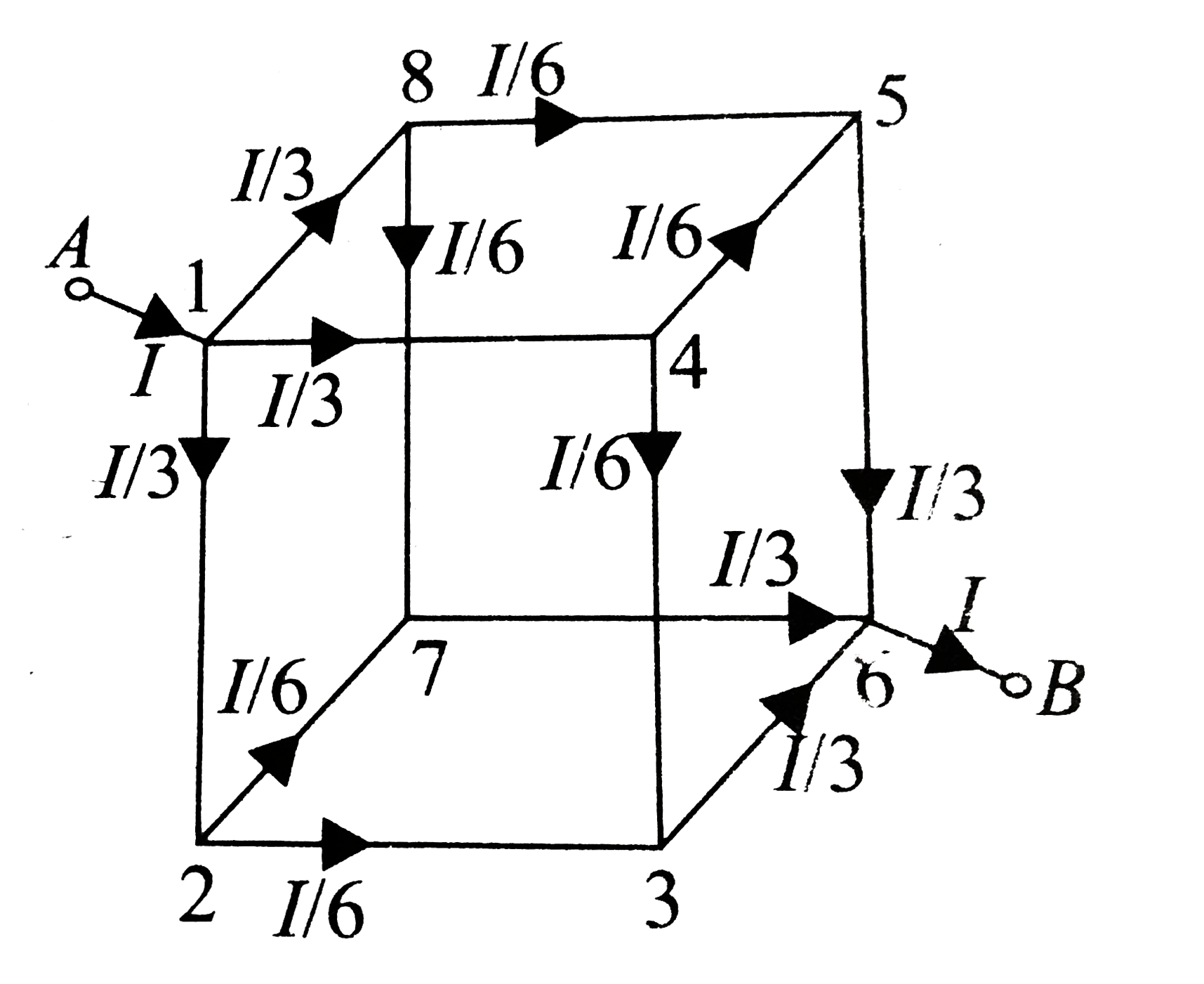
Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in.

Let un number the corners as 1,2,3,…. As
shown in fig 5.46 Let us identify various paths from A to B
a(1−8−7−6),b(1−2−7−6),c(1−8−5−6),<br>d(1−2−3−6),e(1−4−5−6),f(1−4−3−6)
Now for each of these paths
we have identical resistances. Let
the current entering at point A be
I. The current will be distributed
equally among all the three paths.
therefore, we can say that current
is I12=I23=12(I3)=I6
Similarly, we can say that I43=I45=I85=I87=I/6. Therefore, to
calculate the potential difference across the paht (1→2→7→6),
we have
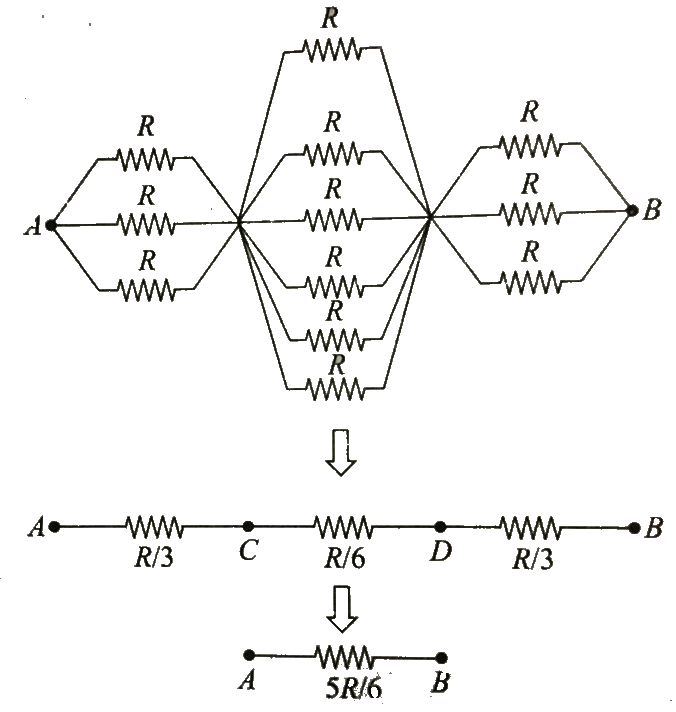
V1−I3R−I6R−I3R=V6
or V1V6=I[R3+R6+R3]=56IR
or(V1−V6)I=56R
Therefore, the equivalent resistance is 5R/6.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in.

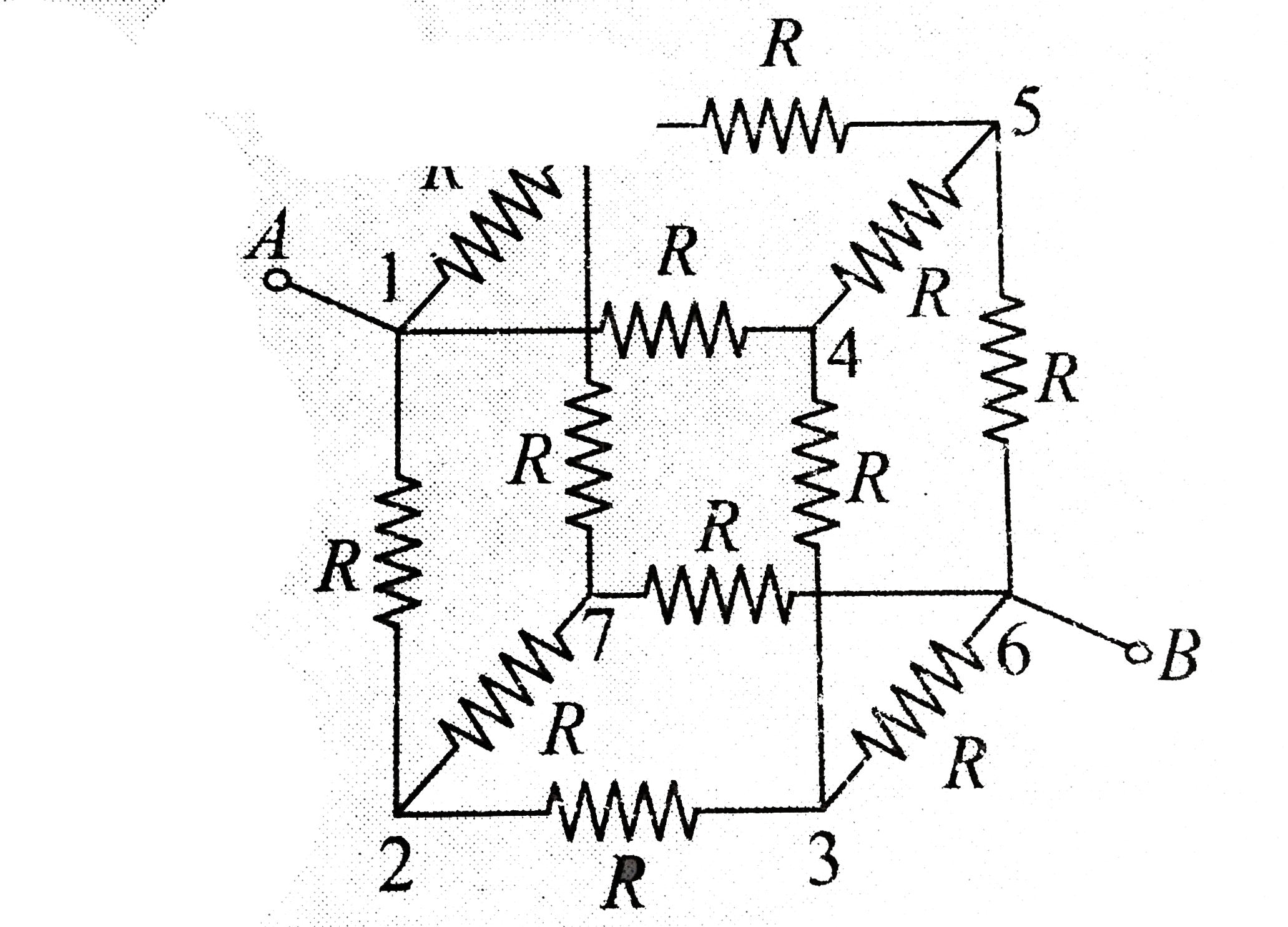
View SolutionTweleve indentical resistor are arranged on all edfges of a cube. Then find the equivalent resistance between the corners 1 and 6 as shwon in fig 5.126(us nodal method)
View Solution
Knowledge Check
Five resistors are connected as shown in the diagram. The equivalent resistance between A and B is
 A6ohmB9ohmC12ohmD15ohm
A6ohmB9ohmC12ohmD15ohmA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
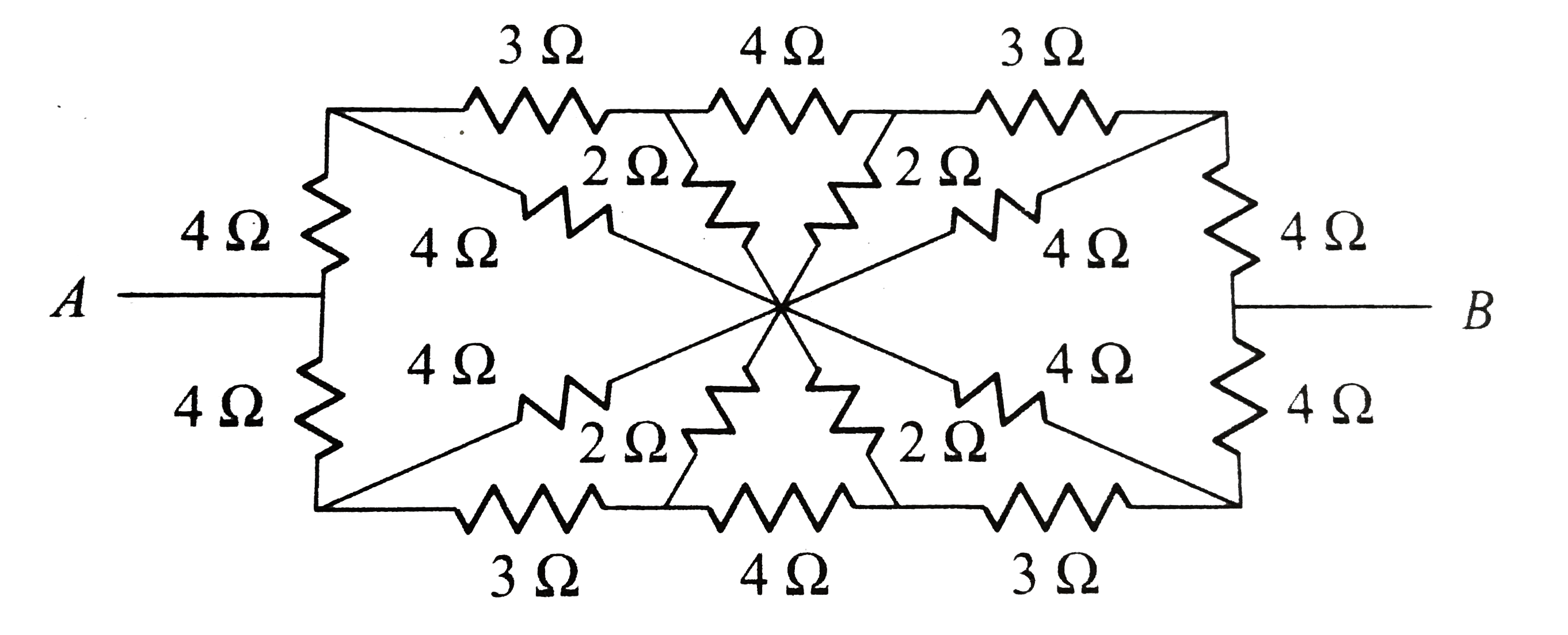 A6ΩB12ΩC9ΩD15Ω
A6ΩB12ΩC9ΩD15ΩEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
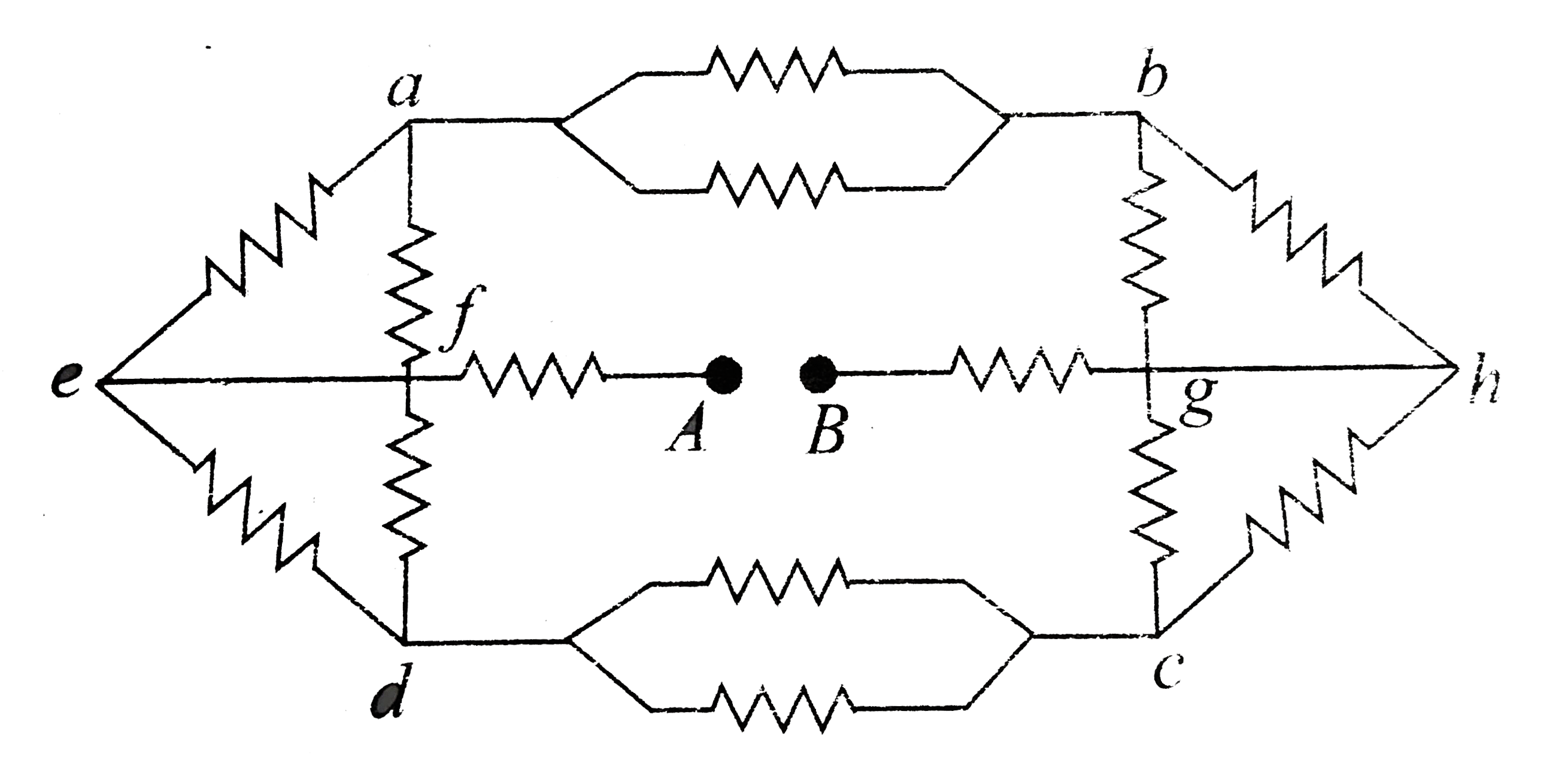 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4
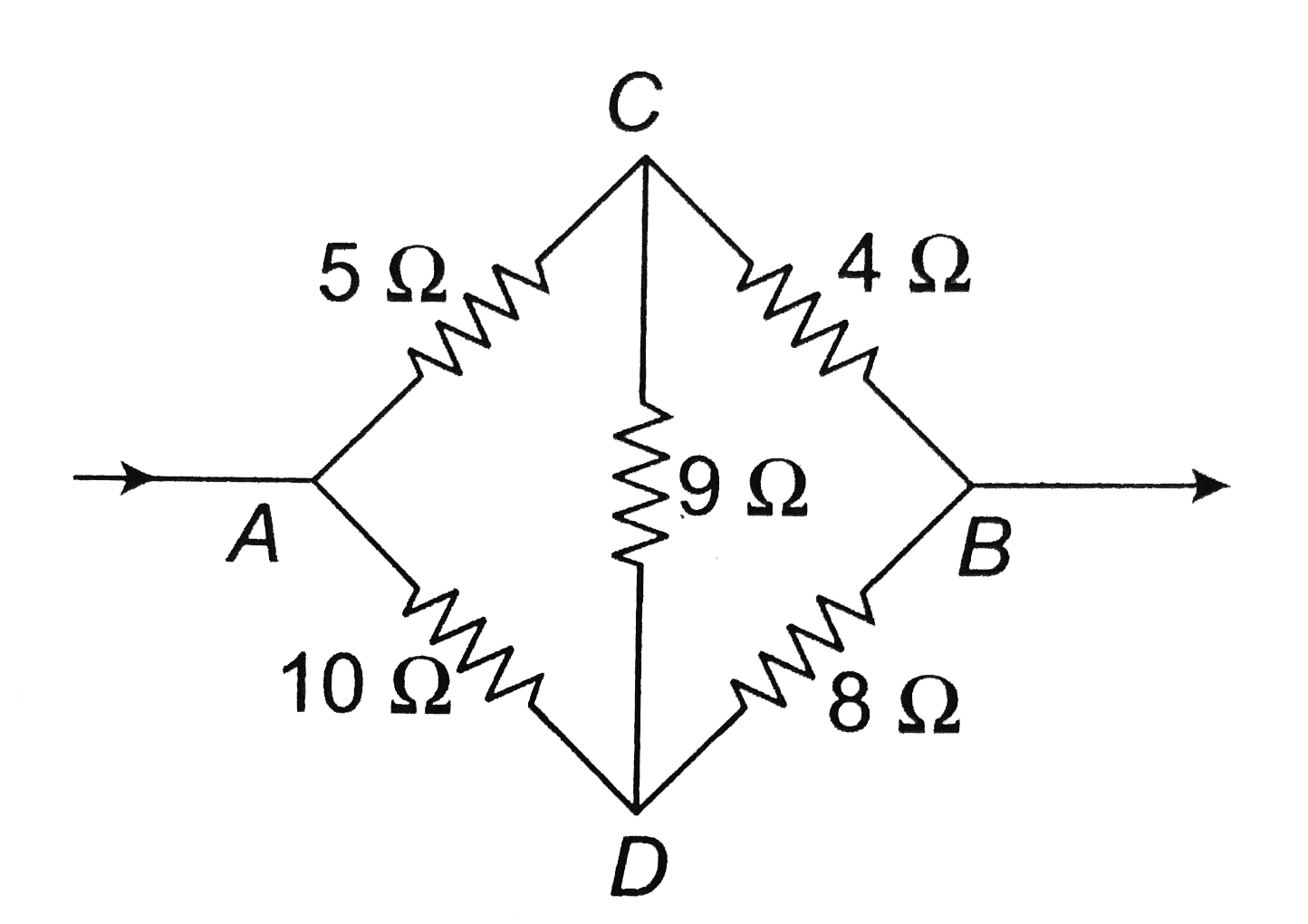
Find equivalent resistance between points A and B in the circuit shown.
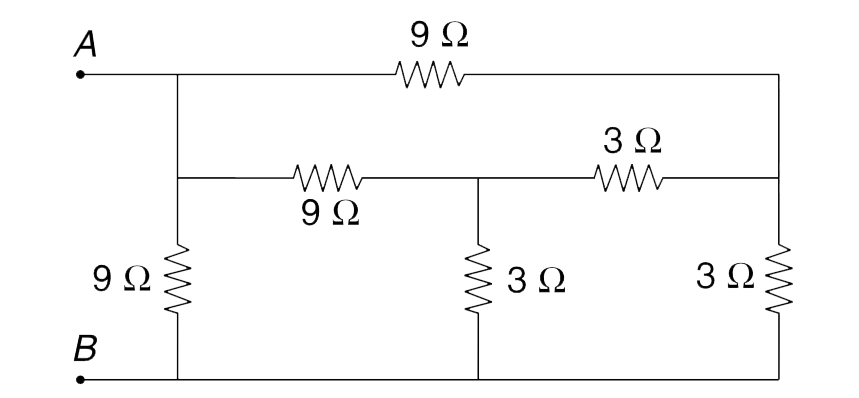
View SolutionFive resistors are connected as shown in figure. Find the equivalent resistance between the points B and C.
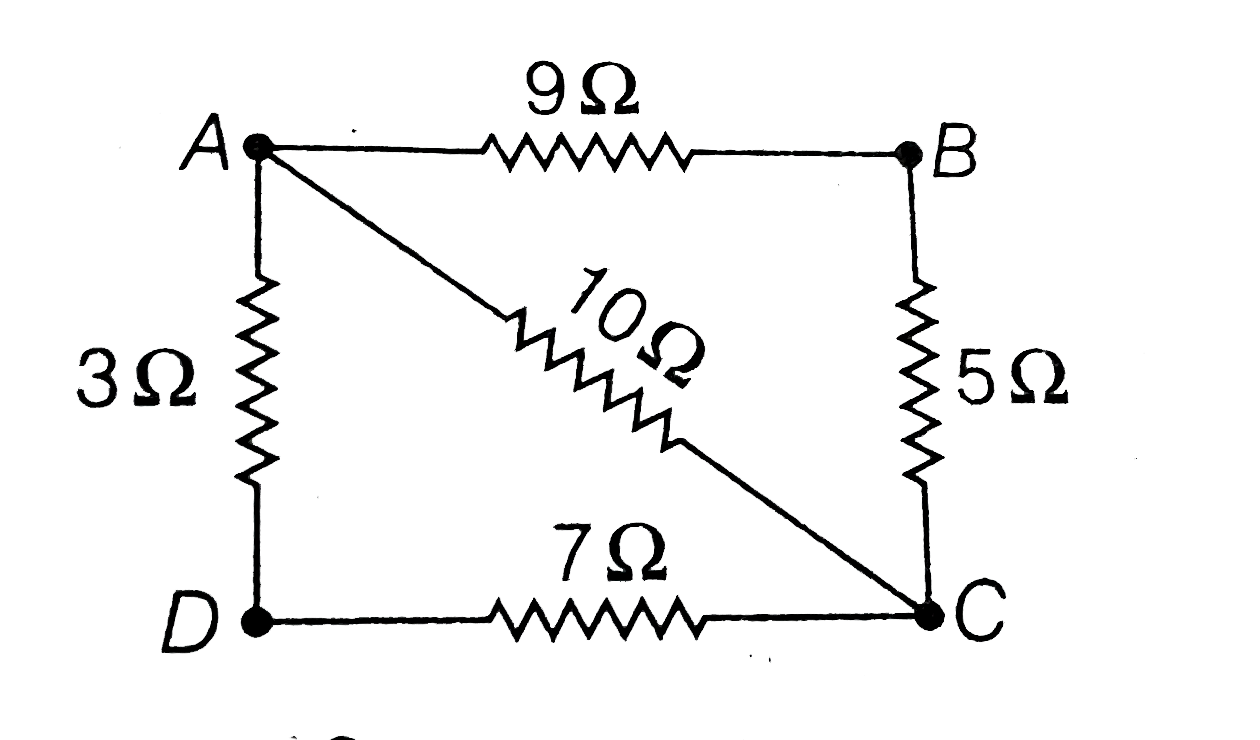
View SolutionFind the equivalent resistance between A & B if all resistance are 'R' ?
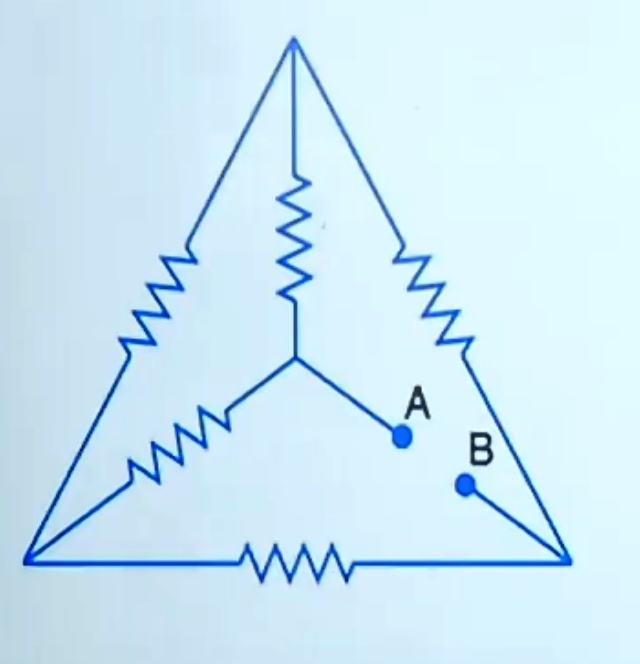
View SolutionFind the equivalent resistance between the point a and b of the circuit shown in figure
View SolutionFind the equivalent resistance between the point a and b of the network shown in figure.

View Solution