The electrical potential function for an electrical field directed parallel to the x - axis is shown in (Fig. 3.152).
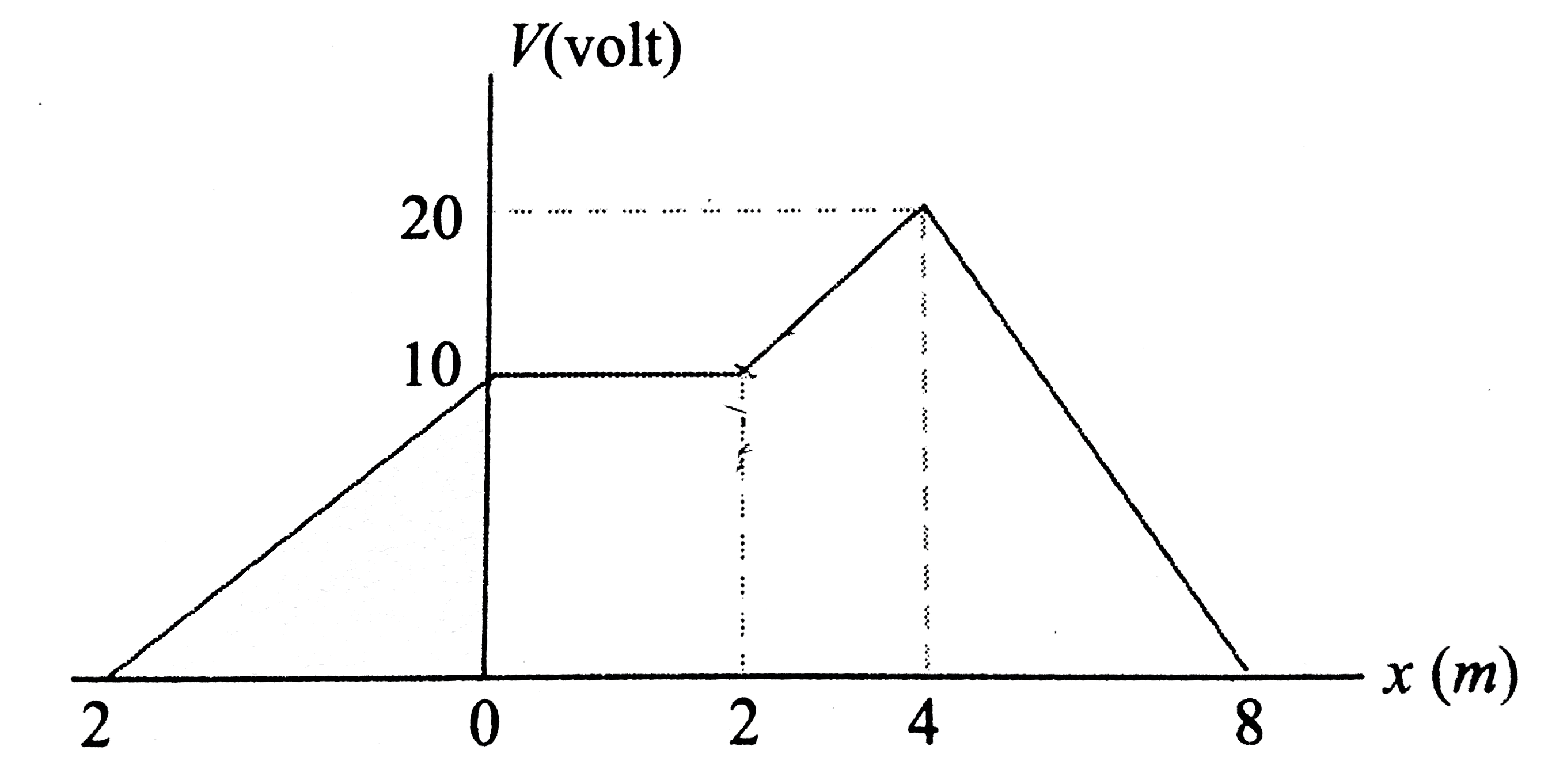 .
.
The magnitude of the electric field in the x - direction in the interval is
The correct Answer is:B
For
For
For
For
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Integer
Explore 5 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.1
Explore 14 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Multiple Correct
Explore 10 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
The electrical potential function for an electrical field directed parallel to the x-axis is shown in the given graph.
 Draw the graph of electric field strength.
Draw the graph of electric field strength.
View SolutionThe variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis.
 .
.
View Solution
Knowledge Check
Variation of electrostatic potential along the x - direction is shown in (Fig. 3.142). The correct statement about electric field is
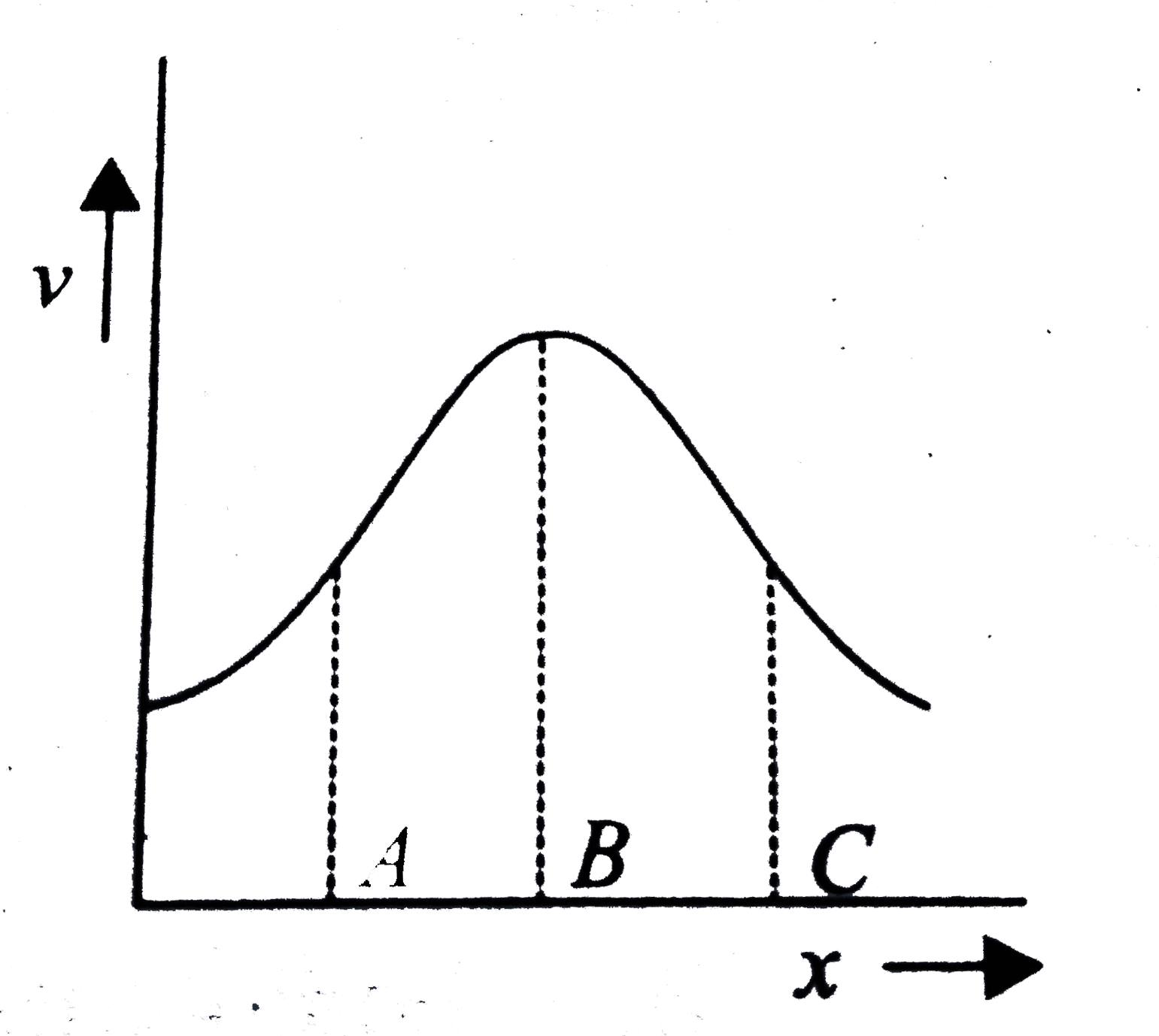 .Ax - component at point B is maximumBx - component at point A is toward positive x - axisCx - component at point C is along negative x - axisDx - component at point C is along positive x - axis
.Ax - component at point B is maximumBx - component at point A is toward positive x - axisCx - component at point C is along negative x - axisDx - component at point C is along positive x - axisDue to an electric dipole shown in fig., the electric field intensity is parallel to dipole axis :
 Aat P onlyBat Q onlyCboth at P and at QDneither at P nor at Q
Aat P onlyBat Q onlyCboth at P and at QDneither at P nor at QElectric potential at any point is V=−6x+2y+9z, then the magnitude of the electric field is
A3√2B4√2C5√2D11
What is the convention for direction of an electric field?'
View SolutionThe electric potential is V=(x2−2x). What is the electric field strength at x=1?
View SolutionThe variation of potential with distance x from a fixed point is shown in figure. Find the magnitude of the electric field (in V/m) at x=13m.

View SolutionIn an electric field region, the electric potential varies along the x-axis as shown in the graph. The x components of the electirc field in the regions for the intervals PQ and QR as market in the garph, in N/C, are respectively:

View SolutionElectric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
View Solution
