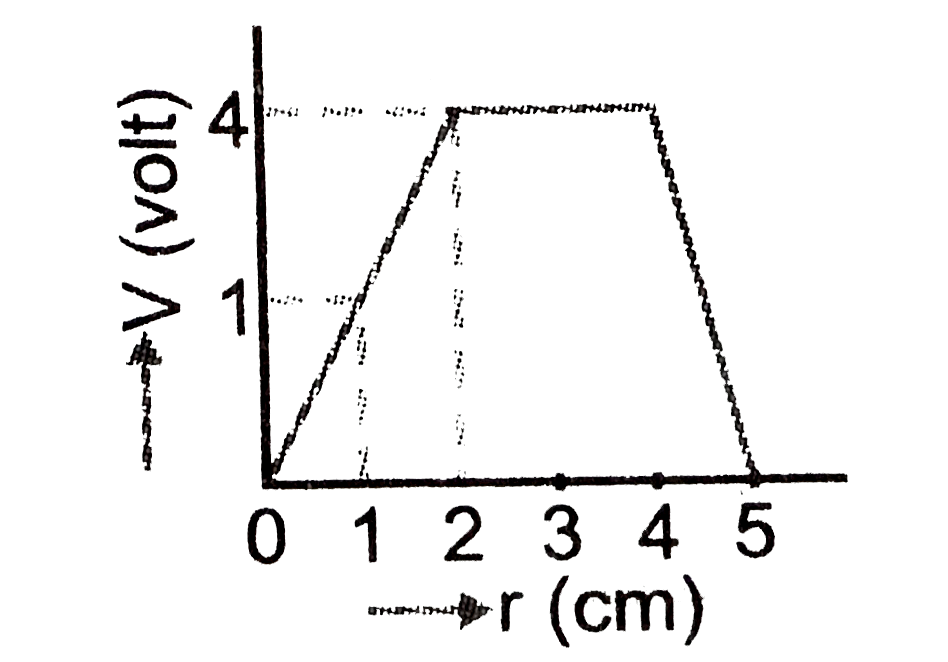The variation of potential with distance x from a fixed point is shown in figure. Find the magnitude of the electric field (in V/m) at x=13m.

The correct Answer is:5
E=−dVdx=204=5volt/meter
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-01
Explore 87 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:SUBJECTIVE QUESTION
Explore 9 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Knowledge Check
The variation of electric potential with distance from a fixed point is shown in figure. What is the value of electric field at x=2m -
 AZeroB6/2C6/1D6/3
AZeroB6/2C6/1D6/3The variation of potential with distance R from a fixed point is shown in figure. The electric field at R = 5 m is -
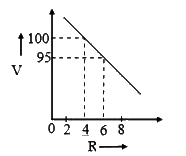 A2.5Vm−1B−2.5Vm−1C(2/5)Vm−1D−(2/5)Vm−1
A2.5Vm−1B−2.5Vm−1C(2/5)Vm−1D−(2/5)Vm−1The variation of potential with distance R from the fixed point is shown in (Fig. 3.125).
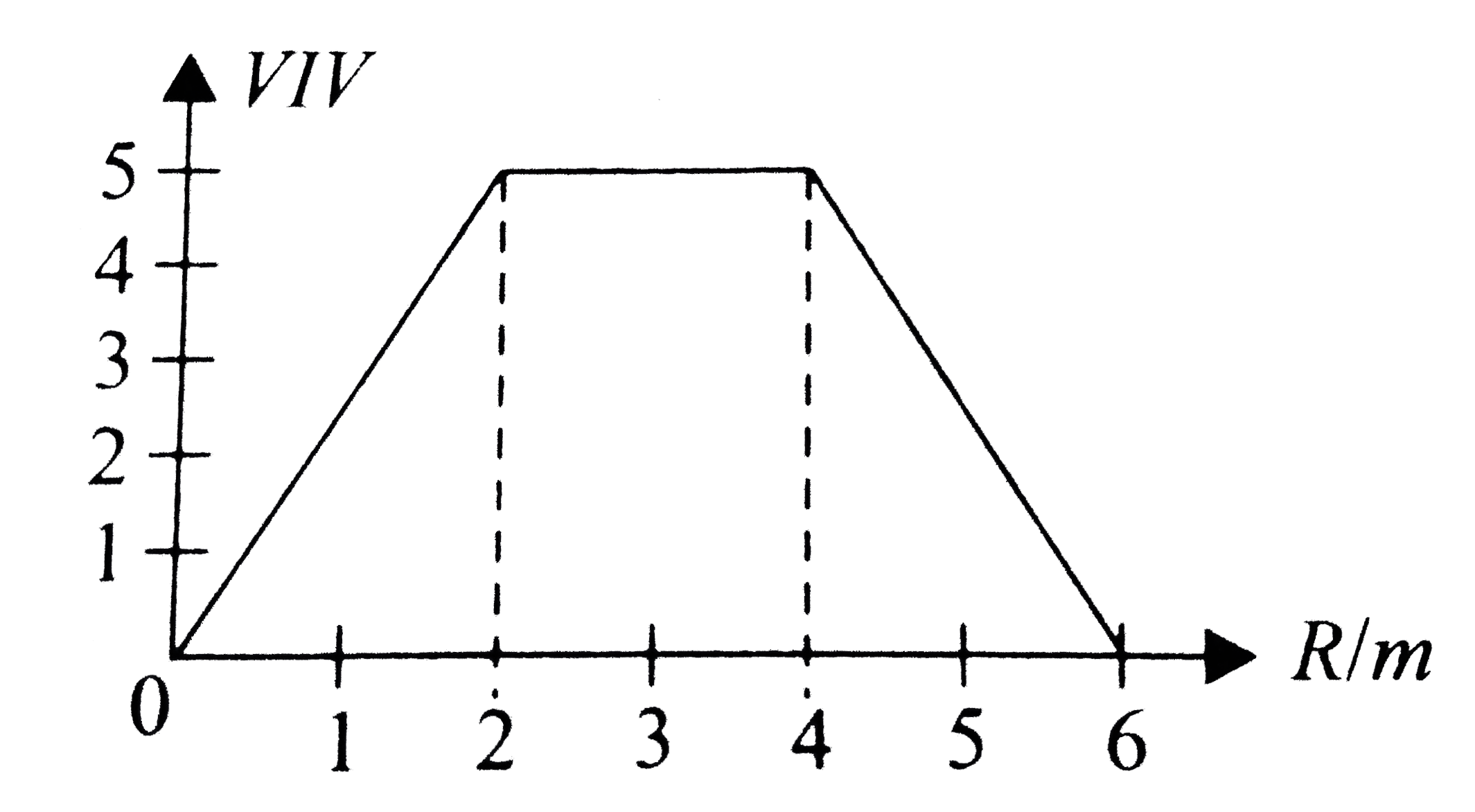 .
.
The electric field at R=5m is.A2.5Vm−1B−2.5Vm−1C0.4Vm−1D−0.4Vm−1
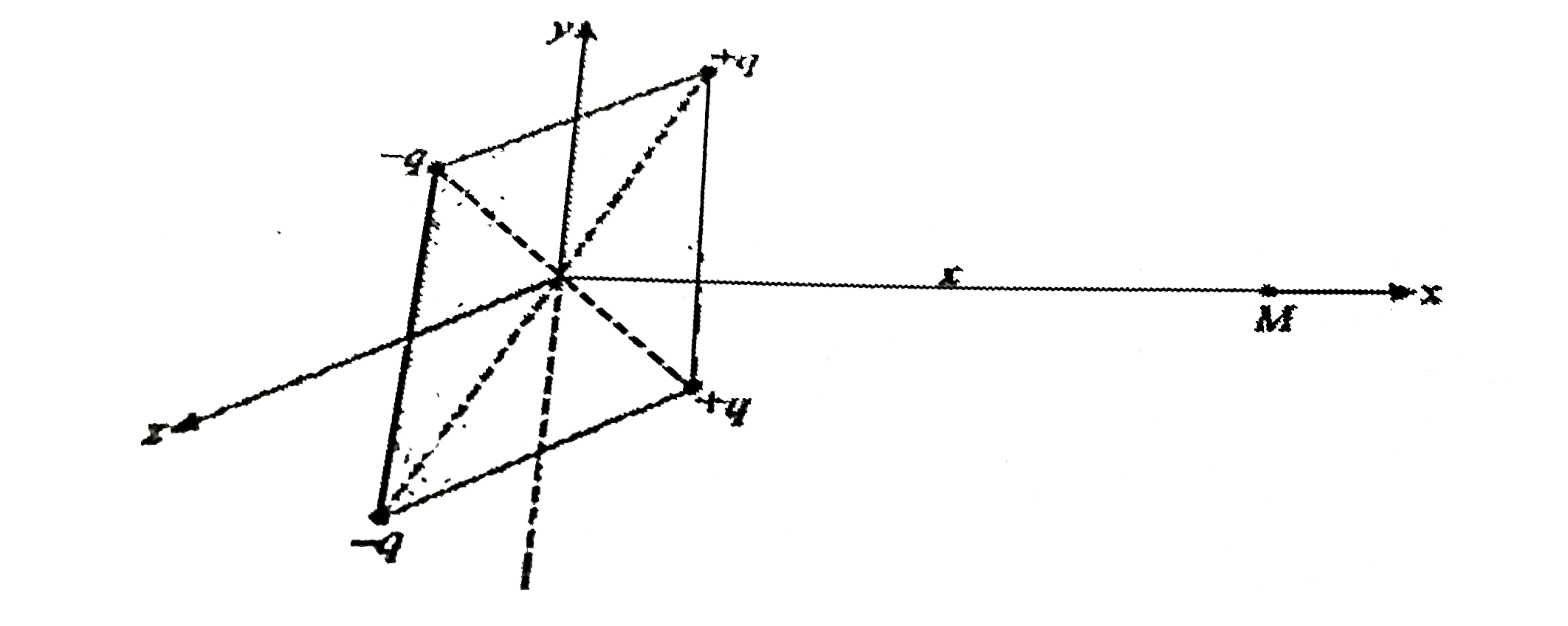
Point charges q and -q located at the vertices of a square with diagonals 2l as shown in figure. Find the magnitude of the electric field at a point located symmetrically with respect to the vertices of the square at a distance x from its centre. Consider x>>l0
[−ql√2πε0x3]
View SolutionElectric potential at any point in a region is given as
V=5x+3y+√15z
In this region the magnitude of the electric field is:
View SolutionThe variation of potential with distance R from a fixed point is as shown below. A charge - q is put at R = 3 m and released. The charge will

View SolutionElectric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
View SolutionElectric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
View Solution