Electric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
3√2
4√2
5√2
7
The correct Answer is:D
To find the magnitude of the electric field from the given electric potential V=−5x+3y+√15z, we will follow these steps:
Step 1: Identify the electric field components
The electric field E is related to the electric potential V by the following equations:
Ex=−∂V∂x,Ey=−∂V∂y,Ez=−∂V∂z
Step 2: Calculate the partial derivatives
1. Calculate Ex:
Ex=−∂V∂x=−∂∂x(−5x+3y+√15z)=−(−5)=5
2. Calculate Ey:
Ey=−∂V∂y=−∂∂y(−5x+3y+√15z)=−3
3. Calculate Ez:
Ez=−∂V∂z=−∂∂z(−5x+3y+√15z)=−√15
Step 3: Write the electric field vector
Now we can express the electric field vector E:
E=(Ex,Ey,Ez)=(5,−3,−√15)
Step 4: Calculate the magnitude of the electric field
The magnitude of the electric field |E| is given by:
|E|=√E2x+E2y+E2z
Substituting the values we found:
|E|=√52+(−3)2+(−√15)2
Calculating each term:
=√25+9+15=√49=7
Final Answer
The magnitude of the electric field is 7.
---
The electric field E is related to the electric potential V by the following equations:
Ex=−∂V∂x,Ey=−∂V∂y,Ez=−∂V∂z
1. Calculate Ex:
Ex=−∂V∂x=−∂∂x(−5x+3y+√15z)=−(−5)=5
Ey=−∂V∂y=−∂∂y(−5x+3y+√15z)=−3
Ez=−∂V∂z=−∂∂z(−5x+3y+√15z)=−√15
Now we can express the electric field vector E:
E=(Ex,Ey,Ez)=(5,−3,−√15)
The magnitude of the electric field |E| is given by:
|E|=√E2x+E2y+E2z
Substituting the values we found:
|E|=√52+(−3)2+(−√15)2
Calculating each term:
=√25+9+15=√49=7
The magnitude of the electric field is 7.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Euipotentials
45 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
Electric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
A3√2B4√2C5√2D7Electric potential at any point is V=−6x+2y+9z, then the magnitude of the electric field is
A3√2B4√2C5√2D11If the potential function is define as V=(−3x+4y+12z)V, then magnitude of electric field E(x,y,z) is
A16V/mB12V/mC√14V/mD13V/m
Electric potential at any point V=-4x+3y+5z then magnitude of electric field in the space will be
View SolutionElectric potential in space V(x,y,z) = (x2+y2+z2)V
Then the magnitude of electric field strength E at (1m, 0, 2m) in N/C is:
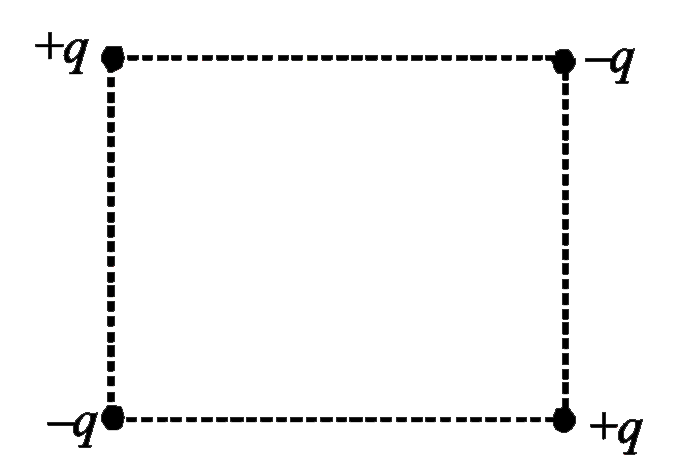
View Solution4Statement - 1 : The electric potential and the electric field intensity at the centre of a square having four fixed point charges at their vertices as shown in figure are zero.
Statement - 2 : If electric potential at a point is zero then the magnitude of electric field at that point must be zero.
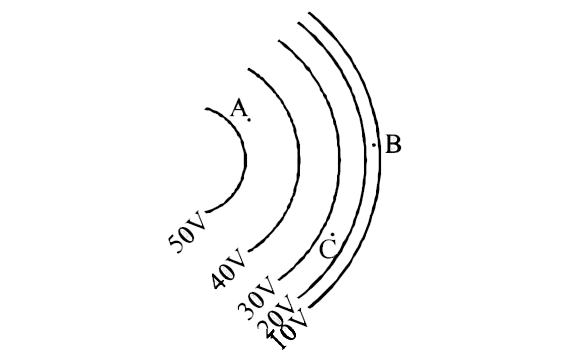
View SolutionFigure shows line of constant potential in a region in which an electric field is present. The values of the potential are written in brackets. Of the points A, B and C, the magnitude of the electric field is greatest at the point………….
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by V=4x2 volts. The electric field at the point (1m, 0, 2m) is……………..V/m.
View Solution
