There is an infinite straight chain of alternating charges and . The distance between teh neighbouring charges is equal to . Find the interaction energy of each charge with all the others.
Instruction . Make use of the expansion of In in a power series in .
none of these.
The correct Answer is:c
=
 .
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Multiple Correct
Explore 10 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Comprehension
Explore 31 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Subjective
Explore 28 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
A point charge q is located at a distance l from an infinite tonducting plane. Find the interaction energy of that charge with chose induced on the plane.
View SolutionEight point charges , each q , are placed on the vertices of a cube of side a. Find the potential energy of the system of charges.
View Solution
Knowledge Check
Two charges of equal magnitudes and at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is
AF/8BF/4C4FDF/16Charges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .A1/2B1/4C2/3D3/4
.A1/2B1/4C2/3D3/4A certain charge Q is divided at first into two parts, q and Q-q. later on the charges are placed at a certain distance. If he force of interaction between two charges is maximum, then
AQq=41BQq=21CQq=31DQq=13
Calculate the interaction energy of two balls whose charges q1 and q2 are spherically. The distanace between teh centres of the balls is equal to l.
View SolutionFind the potential energy of a charge q0 placed at the centre of regular hexagon of side a, if charge q is placed at each vertex of regular hexagon ?
View SolutionThree identical dipoles with charges q and −q, and separation A between the charges, are placed at the corners of an equilateral triangle of side D as shown in fig. Find the interaction energy of the system (a<<d).
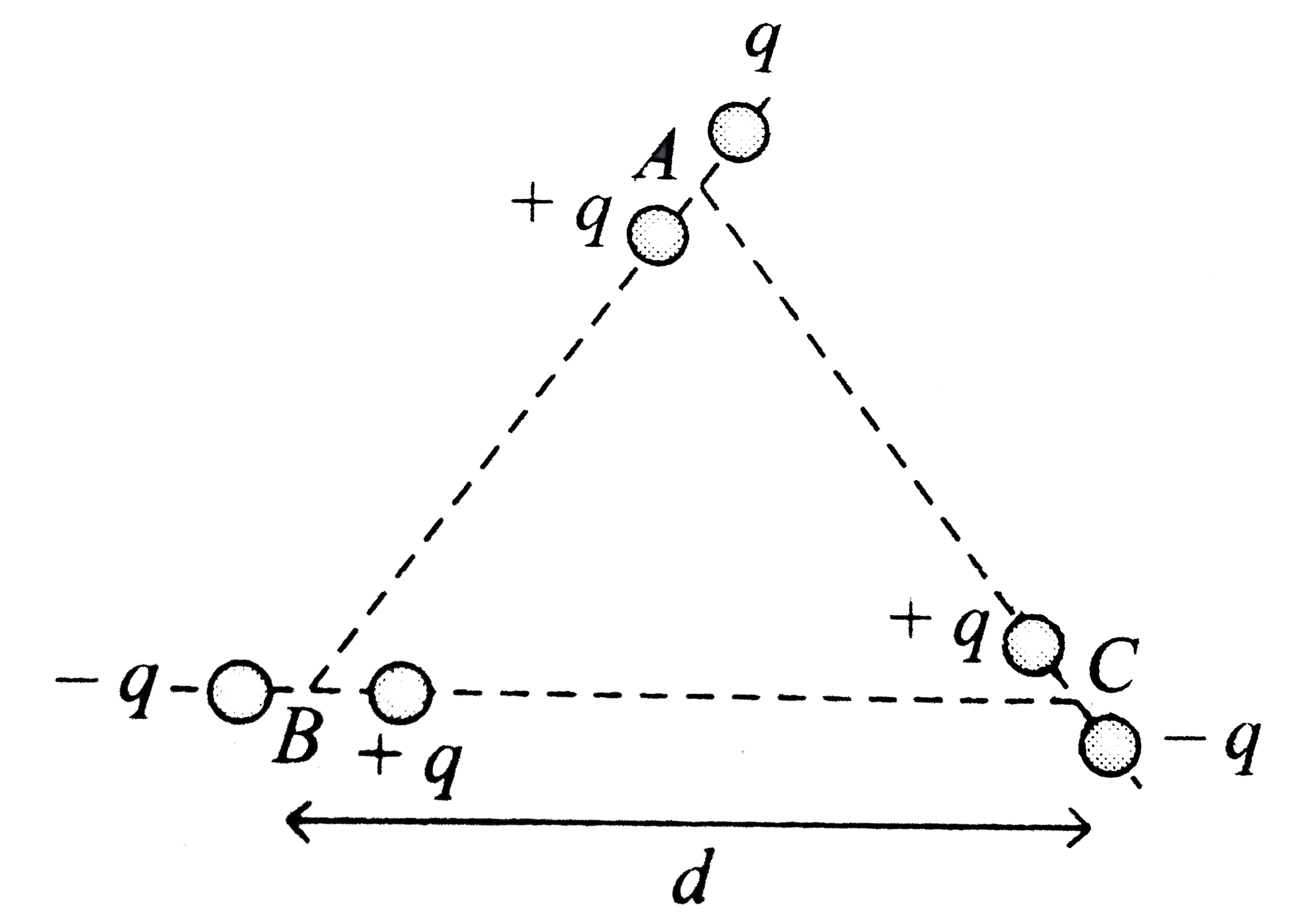 .
.
View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge. Q1 and B a charge Q2. Find the distribution of charges on the four surface.
View SolutionTwo point charges Q1 and Q2 are positioned at points I and 2. The field intensity to the right of the charge Q2 on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
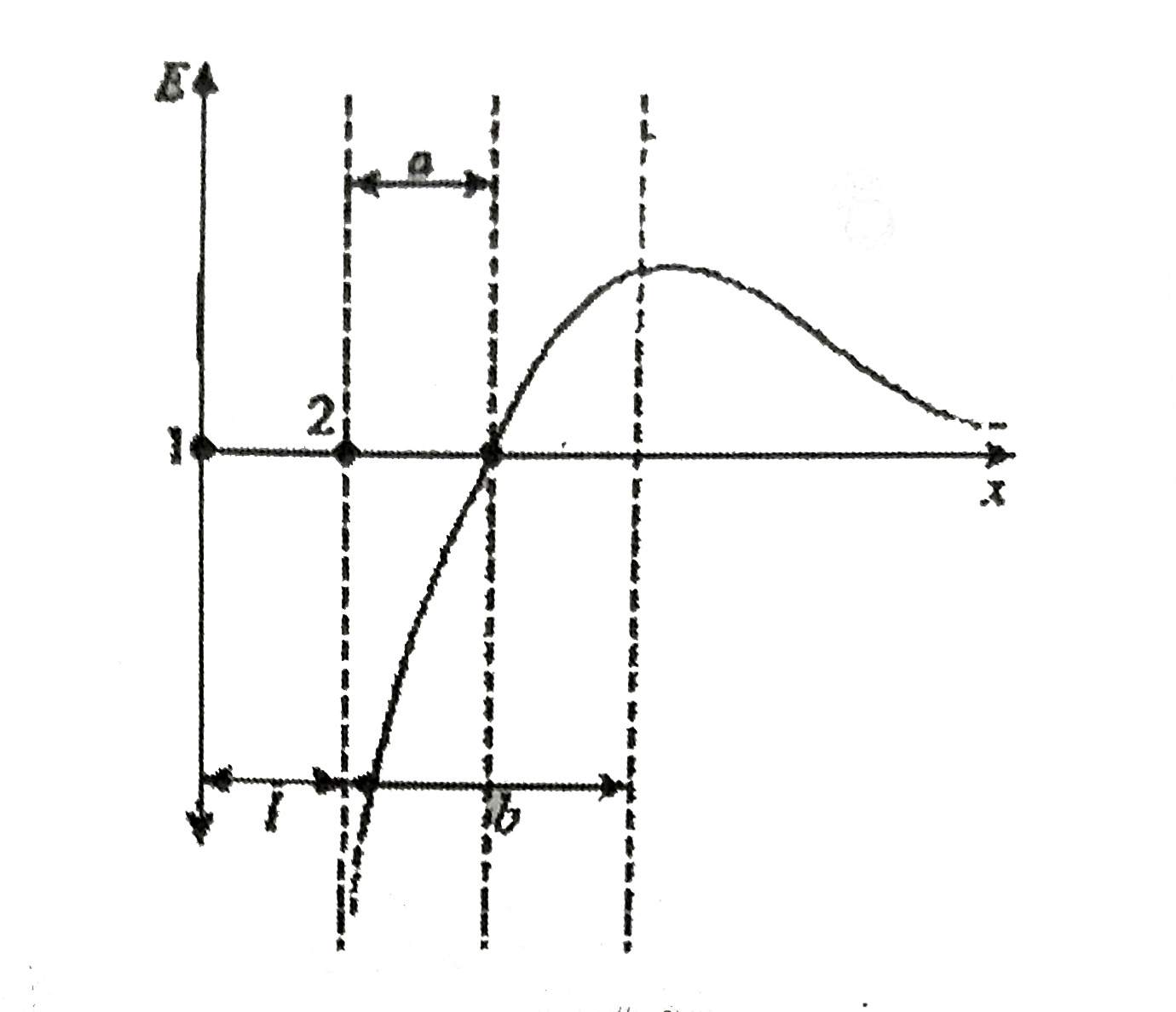
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges ∣∣∣Q1Q2∣∣∣
(c) Find the value of b where the field intensity is maximum
[(a) Q2 is negative and Q1 is positive (b) (l+aa)2, (c) l(l+aa)2/3−1⎤⎥ ⎥ ⎥⎦
View Solution

