A solid conducting sphere of radius 10cm is enclosed by a thin metallic shell of radius 20cm. A charge q=20μC is given to the inner sphere is connected to the shell by a conducting wire.
12 J
9 J
24 J
zero
The correct Answer is:b
To solve the problem, we need to determine the heat generated when the inner conducting sphere is connected to the outer metallic shell by a conducting wire. The heat generated can be calculated based on the change in potential energy of the system.
Step 1: Understand the Configuration
- We have a solid conducting sphere (inner sphere) with a radius of 10 cm and a charge q=20μC.
- This sphere is enclosed by a thin metallic shell (outer shell) with a radius of 20 cm.
Step 2: Determine the Initial Potential of the Inner Sphere
- The potential V of a charged conducting sphere is given by the formula:
V=k⋅qr
where k is Coulomb's constant (k≈9×109N⋅m2/C2), q is the charge, and r is the radius of the sphere.
- For the inner sphere:
Vinner=k⋅qRinner=9×109⋅20×10−60.1=1.8×106V
Step 3: Determine the Potential of the Outer Shell
- When the inner sphere is connected to the outer shell, charge will redistribute until both have the same potential.
- The potential of the outer shell (which is also a conducting surface) is given by:
Vouter=k⋅QRouter
where Q is the total charge on the outer shell.
- Initially, the outer shell has no charge, so:
Vouter=0V
Step 4: Charge Redistribution
- When the inner sphere is connected to the outer shell, charge will flow until both spheres reach the same potential.
- Let Q be the charge that moves to the outer shell.
- The total charge will be conserved:
Qtotal=q+Q=20μC+Q
- The final potential of both the inner sphere and the outer shell must be equal:
Vinner=Vouter
k⋅(20×10−6+Q)0.2=k⋅(20×10−6)0.1
Step 5: Solve for Q
- Simplifying the equation:
20×10−6+Q0.2=20×10−60.1
20×10−6+Q=40×10−6
Q=40×10−6−20×10−6=20×10−6C
Step 6: Calculate the Change in Potential Energy
- The change in potential energy ΔU can be calculated using:
ΔU=12CV2
where C is the capacitance of the system.
- The capacitance C of the system (considering both spheres) can be calculated as:
C=4πϵ0R
where R is the distance between the centers of the spheres.
- For our case:
C=4πϵ0(0.2)=4π(8.85×10−12)(0.2)
C≈2.23×10−11F
- Now, substituting into the potential energy formula:
ΔU=12⋅2.23×10−11⋅(1.8×106)2
Step 7: Calculate the Heat Generated
- The heat generated Qheat is equal to the change in potential energy:
Qheat=ΔU
- We have a solid conducting sphere (inner sphere) with a radius of 10 cm and a charge q=20μC.
- This sphere is enclosed by a thin metallic shell (outer shell) with a radius of 20 cm.
- The potential V of a charged conducting sphere is given by the formula:
V=k⋅qr
where k is Coulomb's constant (k≈9×109N⋅m2/C2), q is the charge, and r is the radius of the sphere.
Vinner=k⋅qRinner=9×109⋅20×10−60.1=1.8×106V
- When the inner sphere is connected to the outer shell, charge will redistribute until both have the same potential.
- The potential of the outer shell (which is also a conducting surface) is given by:
Vouter=k⋅QRouter
where Q is the total charge on the outer shell.
Vouter=0V
- When the inner sphere is connected to the outer shell, charge will flow until both spheres reach the same potential.
- Let Q be the charge that moves to the outer shell.
- The total charge will be conserved:
Qtotal=q+Q=20μC+Q
Vinner=Vouter
k⋅(20×10−6+Q)0.2=k⋅(20×10−6)0.1
- Simplifying the equation:
20×10−6+Q0.2=20×10−60.1
20×10−6+Q=40×10−6
Q=40×10−6−20×10−6=20×10−6C
- The change in potential energy ΔU can be calculated using:
ΔU=12CV2
where C is the capacitance of the system.
C=4πϵ0R
where R is the distance between the centers of the spheres.
C=4πϵ0(0.2)=4π(8.85×10−12)(0.2)
C≈2.23×10−11F
ΔU=12⋅2.23×10−11⋅(1.8×106)2
- The heat generated Qheat is equal to the change in potential energy:
Qheat=ΔU
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Multiple Correct
Explore 10 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Comprehension
Explore 31 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Subjective
Explore 28 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
A solid conducting spere of radius 10cm is enclosed by a thin metallic sheel of radius 20cm. A charge q=20μC is given to the inner spere. Find the heat generated in the process. The inner sphere is connected to the shell by a conducting wire.
 .
.
View SolutionA solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.
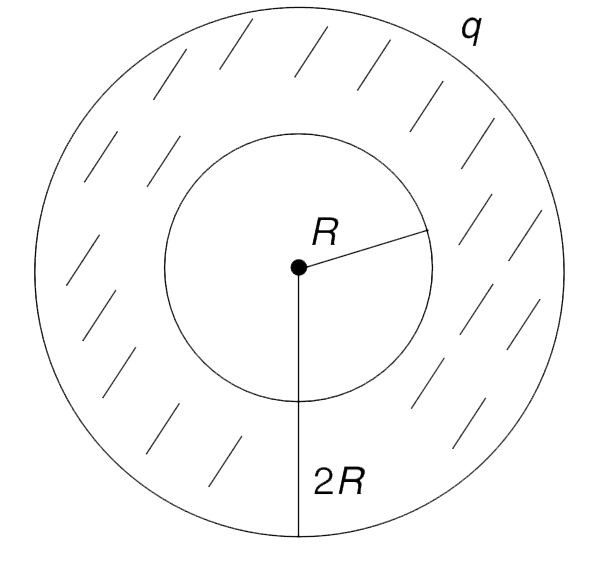
View Solution
Knowledge Check
A solid conducting sphere of radius r is given some charge. Then :
AThe charge is uniformly distributed over its surface, if there is an external electric field.BDistribution of charge over its surface will be non uniform if no external electric field exist in spaceCElectric field strength inside the sphere will be equal to zero only when no external electric field existsDPotential at every point of the sphere must be same in all casesA solid conducting sphere of radius a is enclosed in a concentric shell of radius b>a. The charge on the inner sphere is 3μC and on the conducting shell is −10μC. The potential difference between the conductors is V. If +10μC additional charge is given to the outer shell, the new potential difference is
AVBV/2C2VDzeroFigure shows a solid conducting sphere of radius 1 m. enclosed by a metallic shell of radius 3 m such that their centress coincide. If outer shell is given a charge of 6 μC and inner sphere is earthed, find megnitude charge on the surface of inner shell
 A1μCB2 μCC4 μCD6 μ C
A1μCB2 μCC4 μCD6 μ C
A solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.

View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin unchanged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
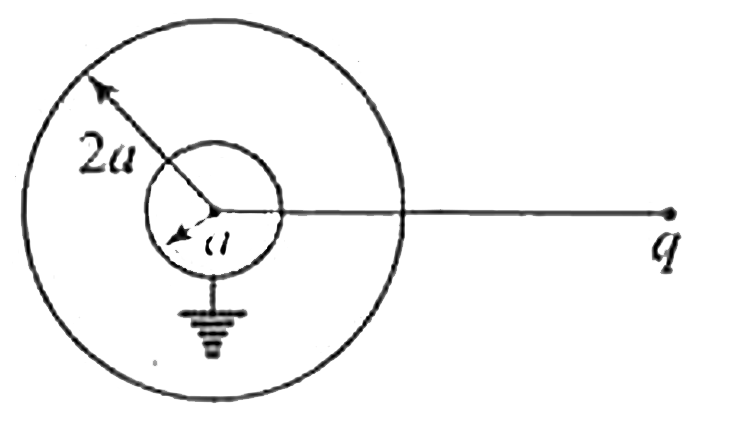
The charge on solid sphere is :
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded

The charge on solid sphere is
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded

The potential of outer shell is
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin unchanged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
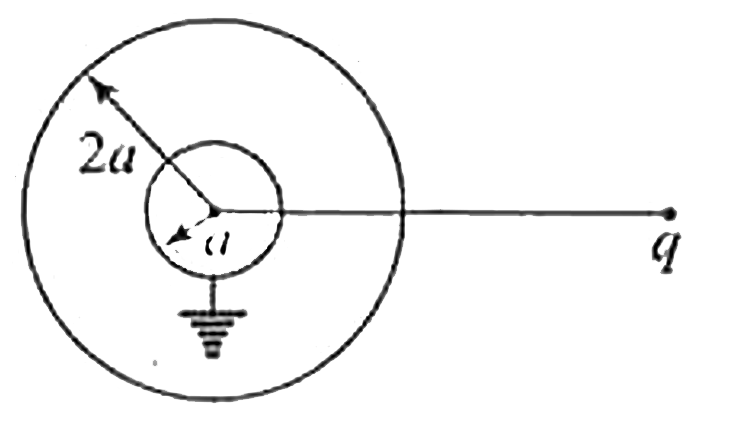
The potential of outer shell is
View Solution

