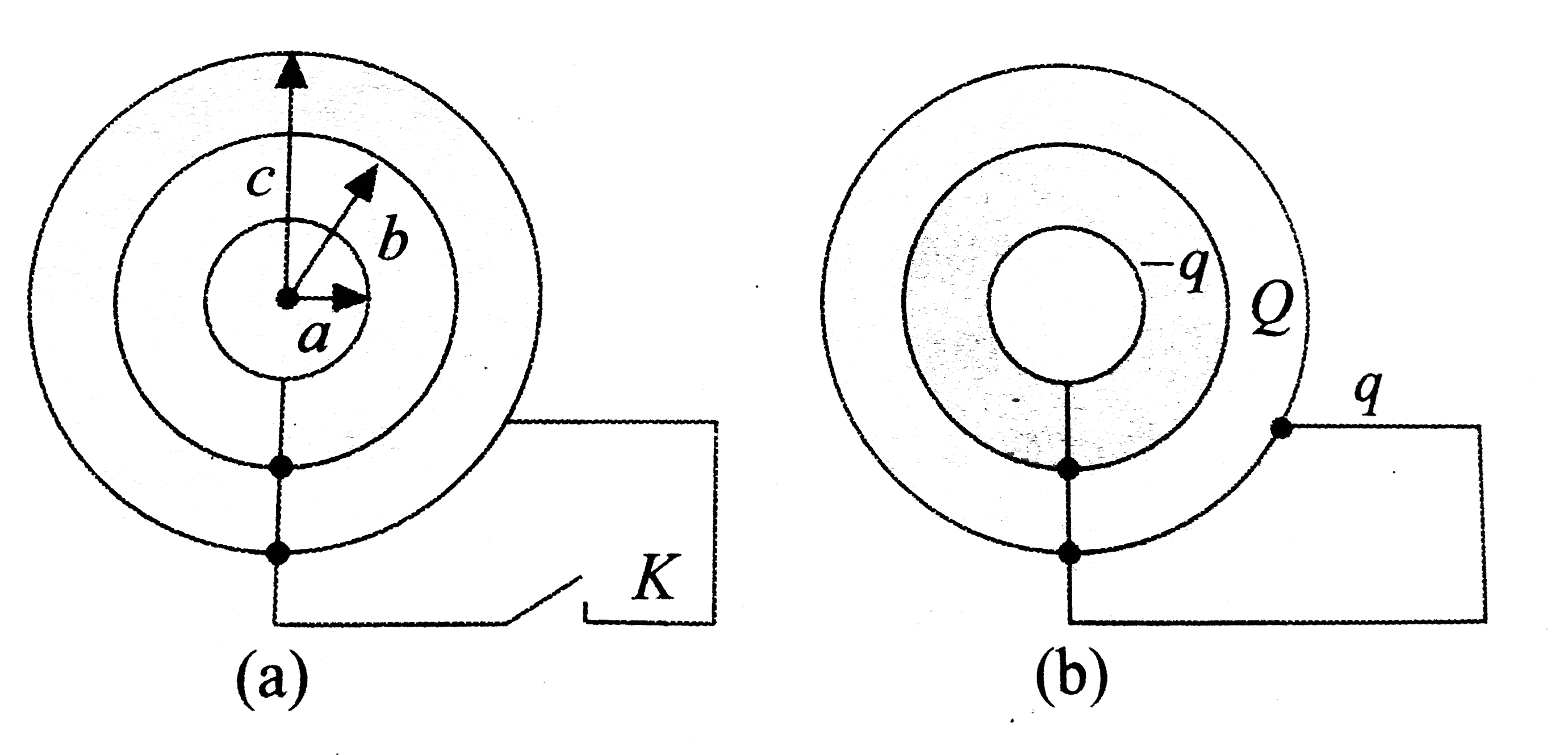
Three concentric conducting shells of radii a, b and c are shown in (Fig. 3.100). Charge on the shell of radius b is Q. If the key K is closed, find the charges on the innermost and outermost shells and the radio of charge densities of the shells. Given that a:b:c=1:2:3.
After closing the key, the innermost and outermost shells will be at the same potential. Let the charge on the outer shell be q and that on the inner shell be (-q), then the total charge on inner and outer shells is zero.
potential on the innermost shell
Va = Sum of potentials due to -q, Q and q
=−qa+Qb+qc
Similarly, the potential on the outermost shell
Vc=qc+Qc+qc
As Va=Vc, we have
−qa+Qb+qc=−qc+Qc+qc
From the given conditions, c=3a,b=2a.
Equation (i) now becomes
−qa+Q2a=−q3a+Q3a
or q=Q4
Thus, the charge on the outermost shell =Q/4, and the charge on the innermost shell is −(Q/4).
σa=14πa2(−Q4)
σb=+Q4πb2=Q4π(4a2)
σc=14πc2(Q4)=+Q16π(9a2).
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Exercise 3.1
Explore 23 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Exercise 3.2
Explore 9 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
There are two thin concentric conducting shells of radii a and b(a<b) . Equal charges Q given to each shell. Find the charge distribution on the inner and outer shell.
View SolutionTwo thin conducting shells of radii R and R ar shown in figure . The outer shell carries a charge +Q and the inner shell is neutral. The inner shell is earthed with the help of switch S . Find the charge attained by the inner shell.
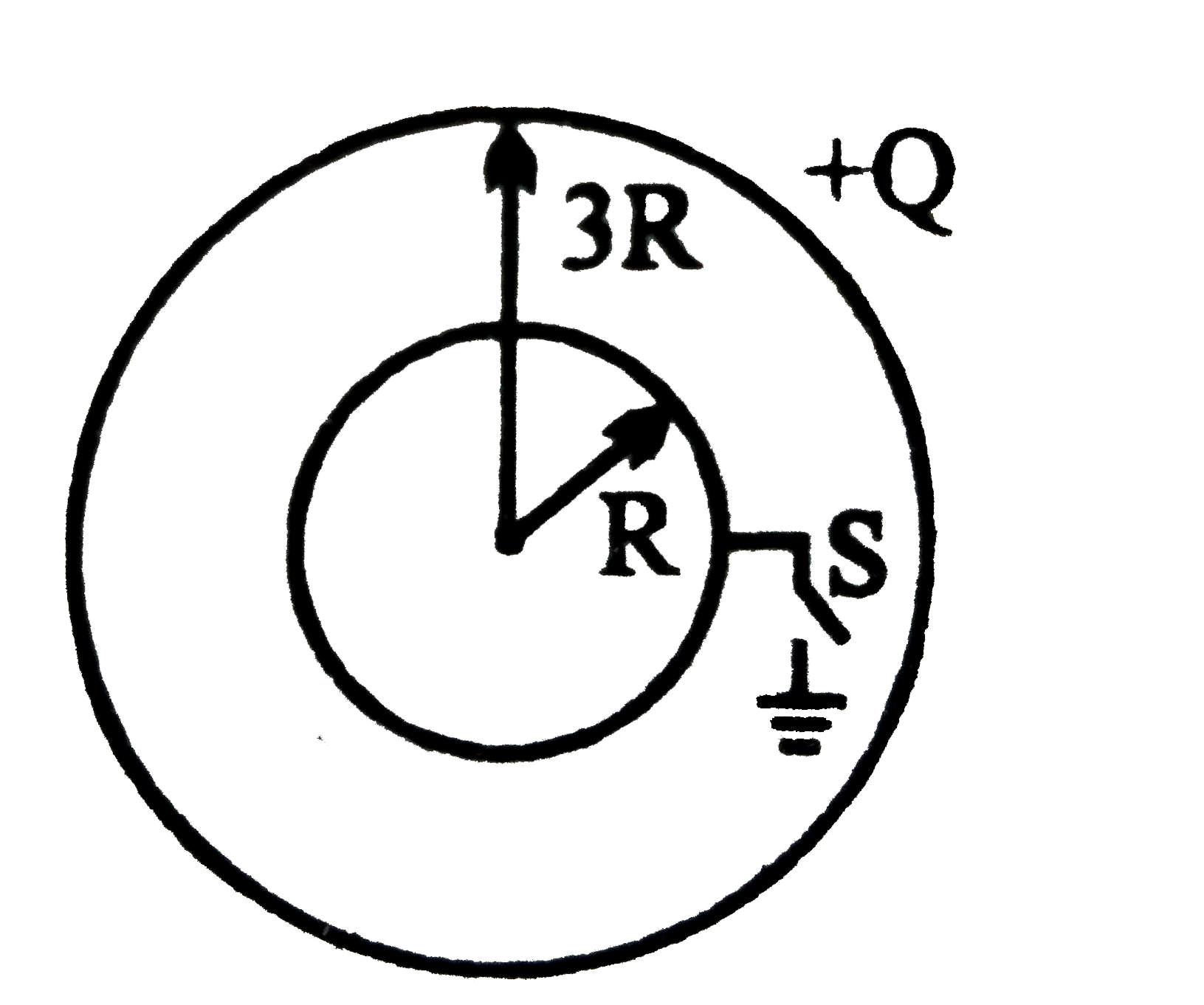 .
.
View Solution
Knowledge Check

Three conducting concentric shell sA,B,andC of radius a,2a,3a are as shown in the figure.The charge on shell B is Q..The switch S is closed.Then after closing the switch
The charge on innermost shell isAQ4B−Q4CQ2D−Q2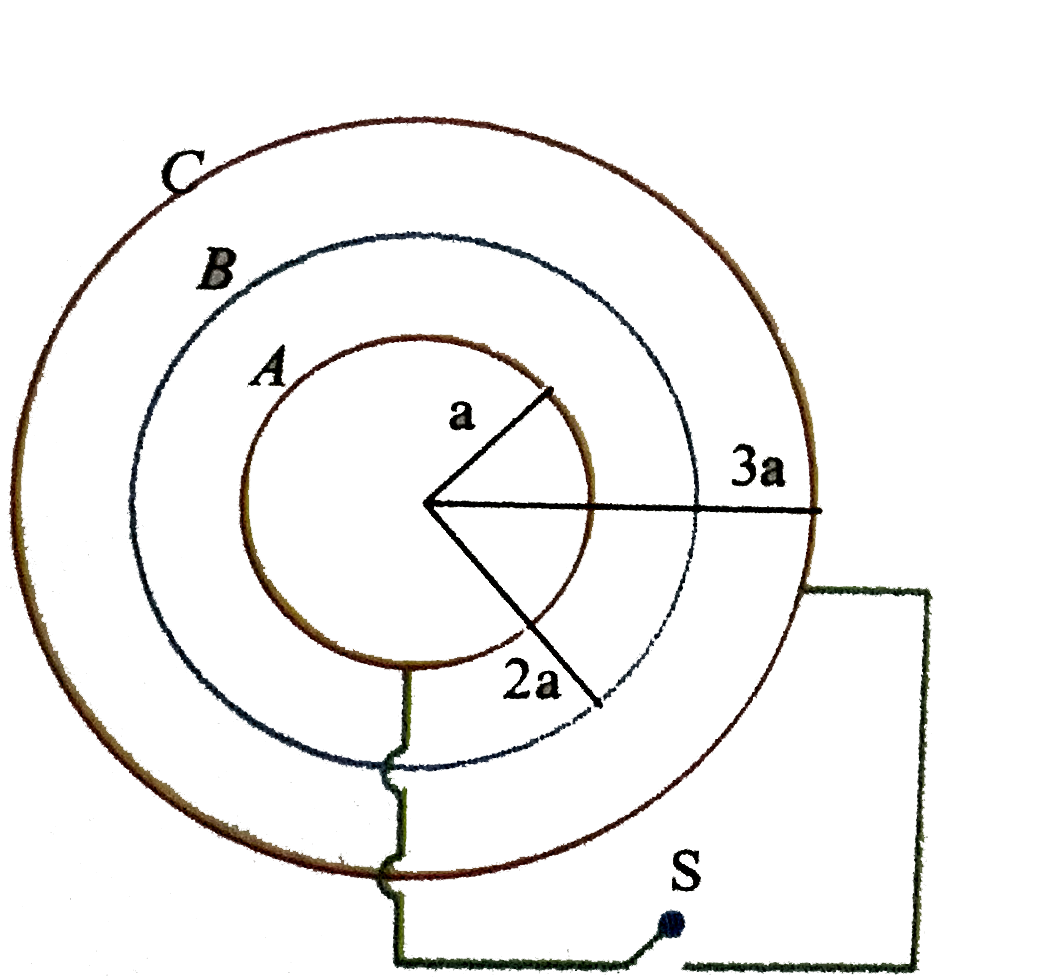
Three conducting concentric shell sA,B,andC of radius a,2a,3a are as shown in the figure.The charge on shell B is Q..The switch S is closed.Then after closing the switch
The charge on outermost shell isAQ4B−Q4CQ2D−Q2Two concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
Aq1=4πε0(ϕ1−ϕ2a2−a1)a1a2Bq1=4πε0(ϕ1+ϕ2a2+a1)a1a2Cq1=πε0(ϕ1−ϕ2a2+a1)a1a2Dq1=2πε0(ϕ1+ϕ2a2−a1)a1a2
In (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionThree concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View SolutionThree concentric conducting spherical shells carry charges +4Q on the inner shell −2Q on the middle shell and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View Solution

