In (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
(i) we know that charges on facing surfaces are equal and opposite. If the charge on the inner sphere is q0, then the charge on the inner surface of the shell should be −q0. Let the charge on the outer surface of the shell be q2. As the shell is earthed, so its potential should be zero. Thus,
Vshell=kq0r2+k(−q2)r2+kq2r2=0 or q2=0
Hence, the charge on the outer surface of the shell is zero. Final charges appearing are shown in (Fig. 3.74) (b)
a.  ,
,
(ii) Potential of inner sphere is
Vi=kq0r1+k(−q0)r2=q04πε0[1r1−1r2].
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Examples
Explore 9 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Exercise 3.1
Explore 23 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
Three conducting spherical shells have radii (a, b, and c) such that a<b<c (Fig. 3.113). Initially, the inner shell is uncharged, the middle shell has a positive charge Q, and the outer shell has a negative charge −Q.
 .
.
a. Find the electric potential of the three shells.
b. If the inner and outer shells are now connected by a wire that is insulated as it passes through the middle shell, what is the electric potential of each of the three shells ? Also, what is the final charge on each shell ?
View SolutionTwo thin conducting shells of radii R and R ar shown in figure . The outer shell carries a charge +Q and the inner shell is neutral. The inner shell is earthed with the help of switch S . Find the charge attained by the inner shell.
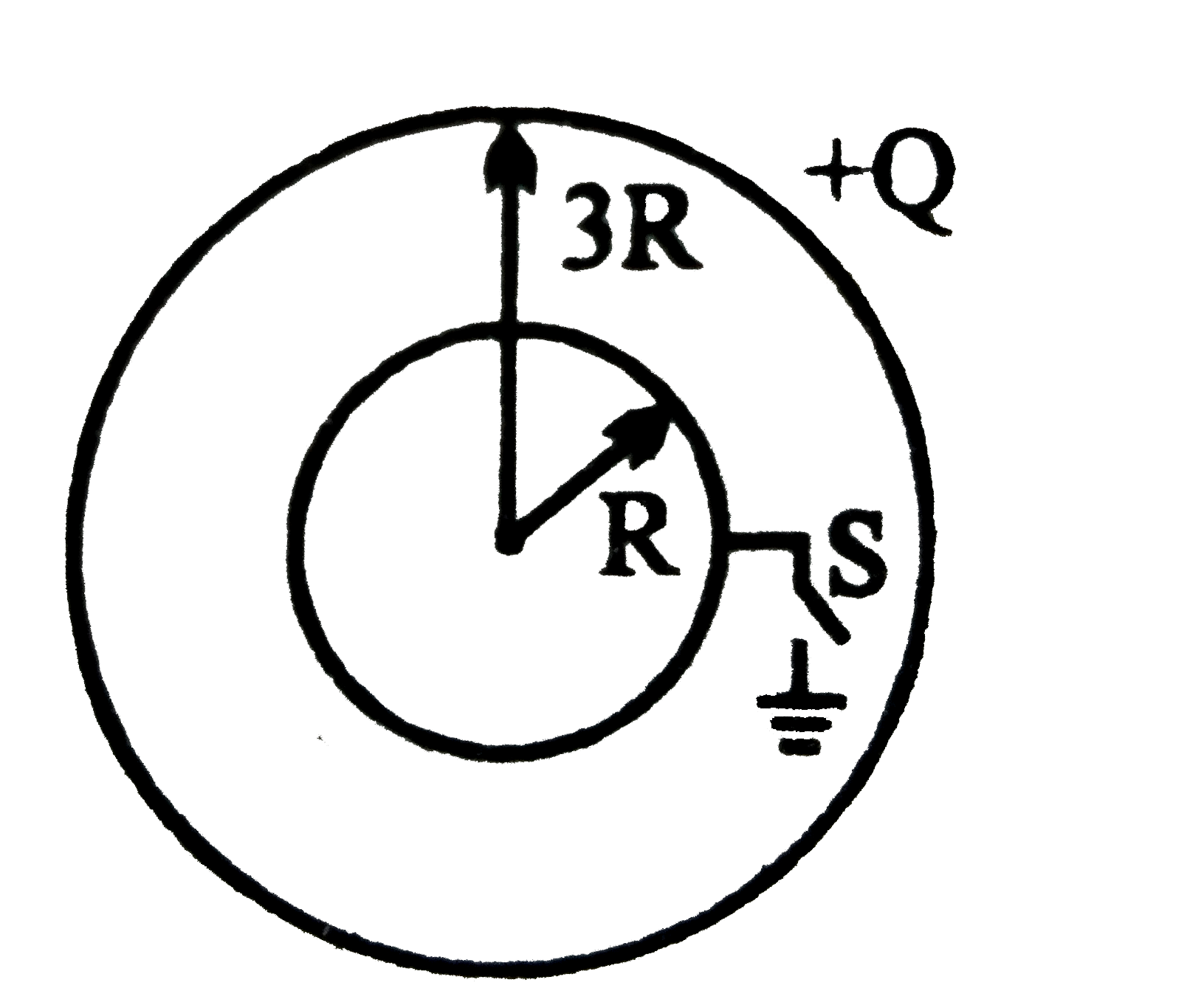 .
.
View Solution
Knowledge Check
A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

The graph of the radial component of E as a function of r will beA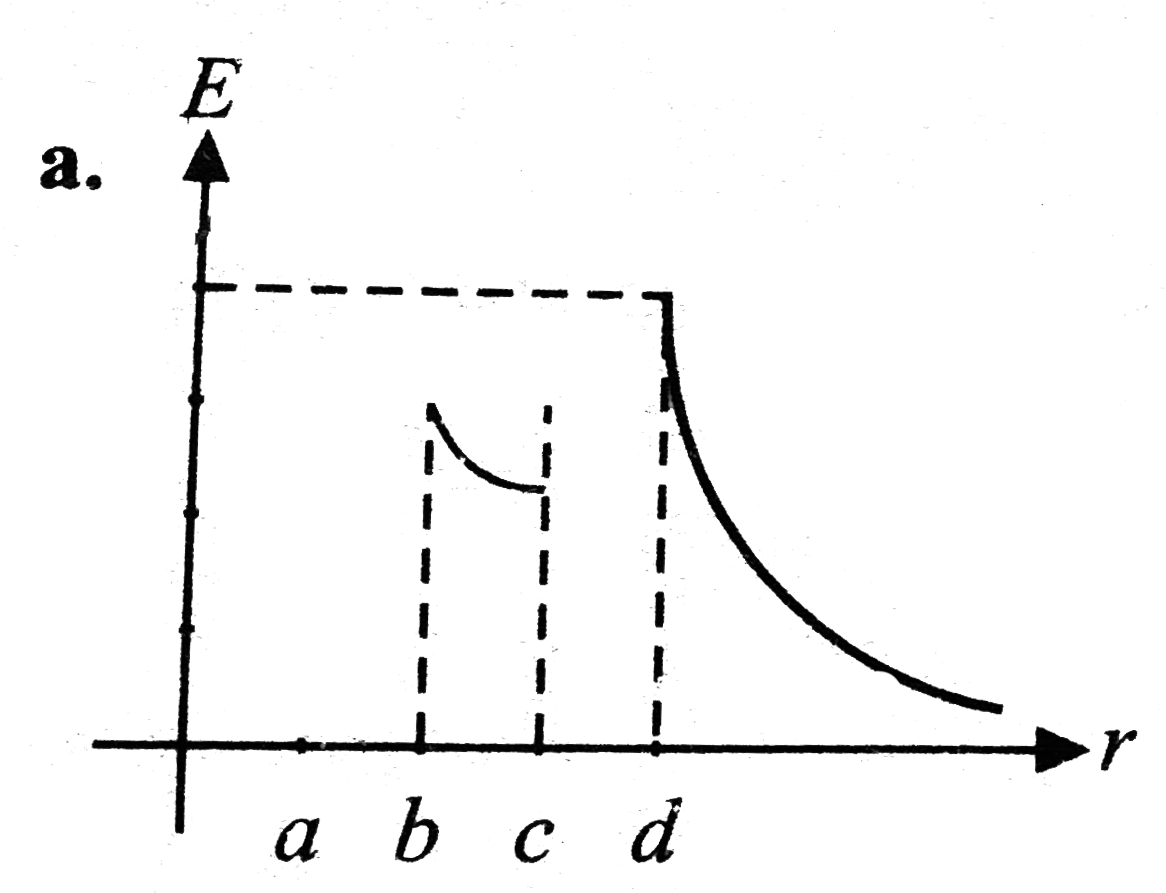 B
B C
C D
D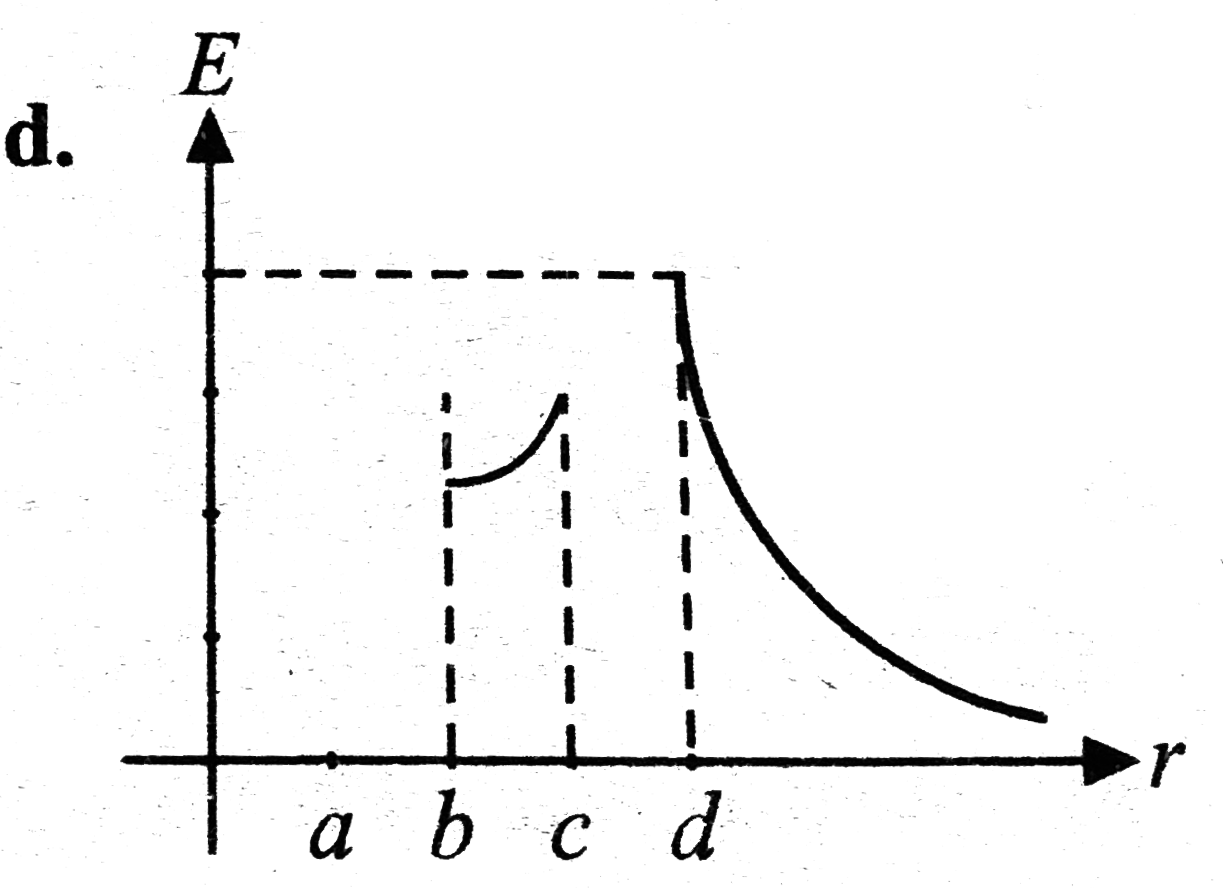
A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

b<r<cAzeroB14πε02qr2C−14πε06qr2D14πε0qr2A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

a<r<bAzeroB14πε02qr2C−14πε06qr2D(1)/( 4 pi epsilon_(0)) (q)/( r^(2))
Consider two concentric spherical metal shells of radii 'a' and b>a .The outer shell has charge Q but the inner shell has no charge.Now the inner shell is grounded ,This means that the inner shell will come at zero potential and that electric fields lines leave the outer shell and end on the inner shell.(a) Find the charge on the inner shell
Find the potential on outer sphere.

View SolutionThere are two concentric metal shells of radii r1 and r2(>r1). If initially, the outer shell has a charge q and the inner shell is having zero charge and then inner shell is grounded. Find :
(i) Charge on the inner surface of outer shell.
(ii) Final charges on each sphere.
(iii) Charge flown through wire in the ground.
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

c<r<d
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r<a
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r>d
View Solution

