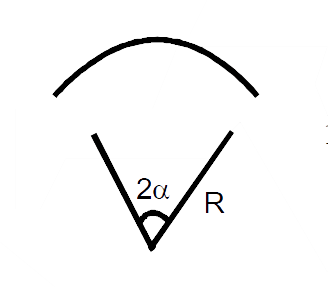
An arc of radius r carries charge. The linear density of charge is λ and the arc subtends an angle π3 at the centre.
λ4ε0
λ8ε0
λ12ε0
λ16ε0
The correct Answer is:C
To solve the problem, we need to find the electric potential V at the center of an arc of radius r that carries a linear charge density λ and subtends an angle π3 at the center.
1. Identify the Length of the Arc:
The length l of the arc can be calculated using the formula:
l=rθ
where θ is the angle in radians. Here, θ=π3.
l=r⋅π3=πr3
Hint: Remember that the length of an arc is given by the product of the radius and the angle in radians.
2. Calculate the Total Charge on the Arc:
The total charge Q on the arc can be found using the linear charge density λ:
Q=λl
Substituting the expression for l:
Q=λ⋅πr3
Hint: The total charge is the product of the linear charge density and the length of the arc.
3. Use the Formula for Electric Potential:
The electric potential V at a distance r from a point charge Q is given by:
V=kQr
where k=14πϵ0.
Hint: Electric potential due to a point charge depends on the distance from the charge and the magnitude of the charge.
4. Substitute for Q:
Now substitute Q into the potential formula:
V=kλ⋅πr3r
Hint: Simplifying the expression will help you to find the final form of the potential.
5. Simplify the Expression:
The r in the numerator and denominator cancels out:
V=k⋅λπ3
Hint: Always look for opportunities to simplify expressions by canceling common factors.
6. Substitute the Value of k:
Substitute k=14πϵ0:
V=14πϵ0⋅λπ3
Hint: When substituting constants, ensure to keep track of all factors.
7. Final Simplification:
Simplifying the expression gives:
V=λ12ϵ0
Hint: Double-check your arithmetic to ensure accuracy in the final expression.
Final Answer:
The electric potential V at the center of the arc is:
V=λ12ϵ0
The length l of the arc can be calculated using the formula:
l=rθ
where θ is the angle in radians. Here, θ=π3.
l=r⋅π3=πr3
The total charge Q on the arc can be found using the linear charge density λ:
Q=λl
Substituting the expression for l:
Q=λ⋅πr3
The electric potential V at a distance r from a point charge Q is given by:
V=kQr
where k=14πϵ0.
Now substitute Q into the potential formula:
V=kλ⋅πr3r
The r in the numerator and denominator cancels out:
V=k⋅λπ3
Substitute k=14πϵ0:
V=14πϵ0⋅λπ3
Simplifying the expression gives:
V=λ12ϵ0
The electric potential V at the center of the arc is:
V=λ12ϵ0
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.4
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
Knowledge Check
The length of an arc of a radius of 14 cm which subtends an angle of 36∘ at the ends centre is
A8.4cmB4.8cmC8.8cmD7.8cmWhich of the following can be the angle subtended by a minor arc at the centre?
A100∘B220∘C180∘D270∘In a circle of radius 21 cm, an arc subtends an angle of 72 at the centre. The length of the arc is
A21.6 cmB26.4 cmC13.2 cmD19.8 cm
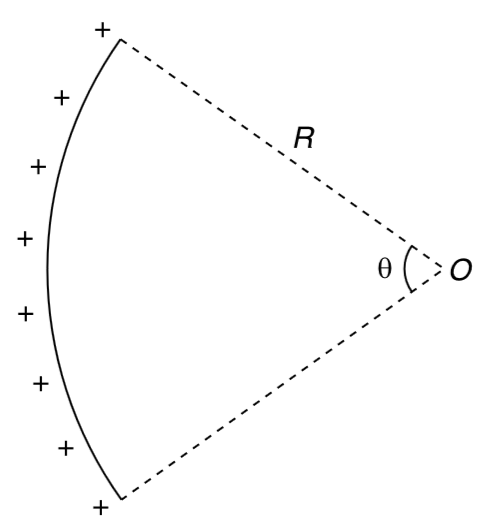
A thread having linear charge density λ is in the shape of a circular arc of radius R subtending an angle θ at the centre.
(a). Find the electric field at the centre.
(b). Using the epression obtained in part (a) find the field at the centre if the thread were emicircular
(c). Find the field at centre using the expression obtained in part (a) for the case θ→0. Is the result justified?
(d). A thread having total charge Q (uniformly distributed is in the shape of a circular arc of radius R subtending an angle θ at centre. write the expression for the field at the center. Obtain the field whenθ→0. Make sure you understand the difference in case. (c) and (d).
View SolutionFind the length of an arc of a circle of radius 10cm subtending an angle of 300 at the centre
View SolutionFind, in terms of π , the length of the arc that subtends an angle of 30o at the centre of a circle of radius 4 cm.
View SolutionIn a circle of radius 21 cm, an arc subtends an angle of 60∘ at the centre. Find the length of the arc.
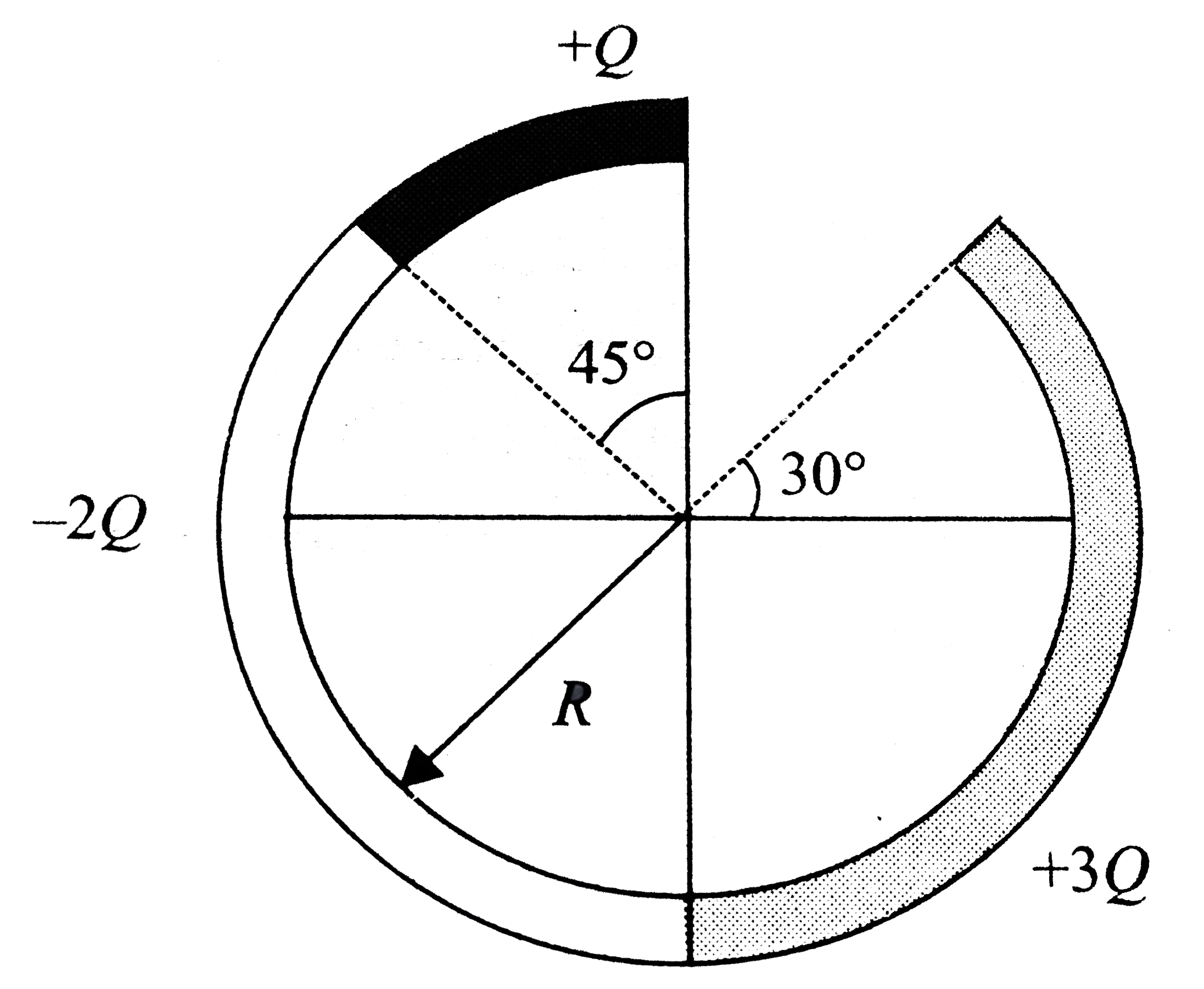
View Solution(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
 .
.
View Solution