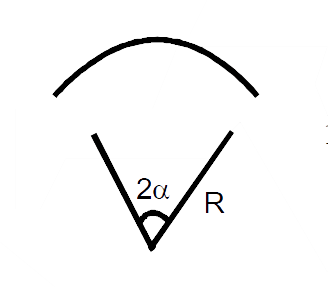
Find the gravitational field strength and potential at the centre of arc of linear mass density $λ$ subtending an angle $2 α$ at the centre.

Video Solution

Text Solution

Verified by Experts

$\frac{2 G λ}{R} (sin α), (- G λ 2 α)$

|

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 3 | Level - II (Subjective | JEE Advanced)
10videos
GRAVITATION
BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 | Level - I (Previous year | JEE Main)
16videos
GRAVITATION
BOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 2 (Level - II) Multiple choice | JEE Advanced
12videos
GRAVITATION
BOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II
55videos
GEOMETRICAL OPTICS
BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced
22videos
HEAT - 1

Similar Questions

Knowledge Check

Question 1 - Select One
The area of segment of a circle of radius $α$ subtending an angle of $2 α$ at the centre is :
A $a^{2} (α + \frac{1}{2} sin 2 α)$
B $\frac{1}{2} a^{2} sin 2 α$
C $a^{2} (α - \frac{1}{2} sin 2 α)$
D $a^{2} α$
Question 2 - Select One
The area of segment of a circle of radius $α$ subtending an angle of $2 α$ at the centre is :
A $a^{2} (α + \frac{1}{2} sin 2 α)$
B $\frac{1}{2} a^{2} sin 2 α$
C $a^{2} (α - \frac{1}{2} sin 2 α)$
D $a^{2} α$
Question 3 - Select One
An arc of radius r carries charge. The linear density of charge is $λ$ and the arc subtends an angle $\frac{π}{3}$ at the centre.
A $\frac{λ}{4 ε_{0}}$
B $\frac{λ}{8 ε_{0}}$
C $\frac{λ}{12 ε_{0}}$
D $\frac{λ}{16 ε_{0}}$

MOTION-GRAVITATION-Exercise - 3 | level - 1 (Subjective | JEE Advanced)

Home
Ask Doubt
Profile