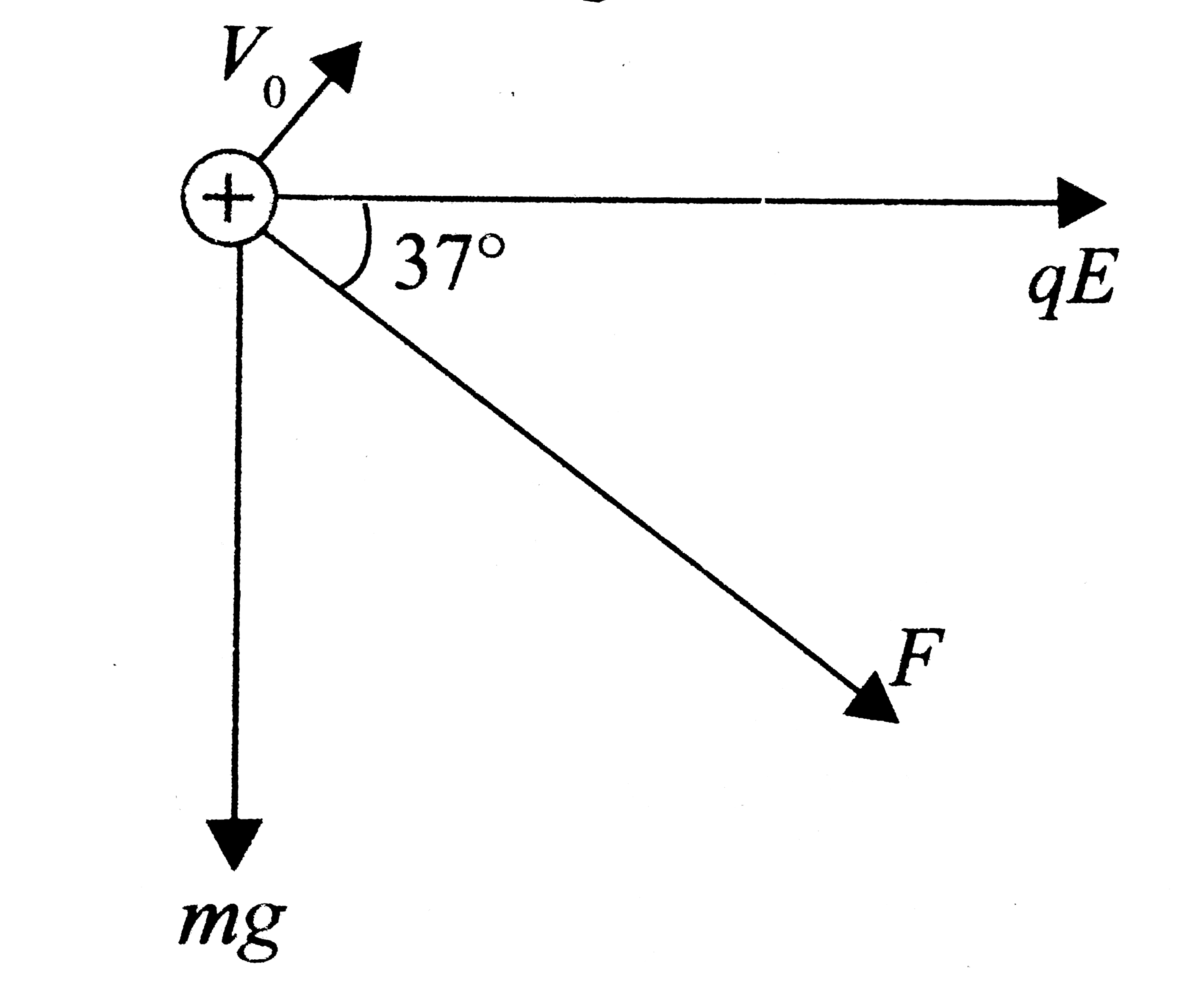
A small sphere of mass carrying a positive charge is connected with a light, flexible, and inextensible string of length and whirled in a vertical circle. If a horizontal rightward electric field of strength exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle .
When a particle having no charge is whirled in a vertical circle, the only force (other than tension in thread) acting on the particle is its weight. It is vertically downward and tension is minimum at the highest point, which is vertically above the center of the circle.
In the pervious illustration, there were two forces mg and qE (other than tension in thread) on the particle were responsible for analysis of critical condition. Their resultant was vertically upward. In that case, tension was minimum at the lowest point of vertical circle, which was vertically below the center of the cercle. It means tension is minimum when the resultant force (other than tension) acting on the particle is toward center.
In the present illustration, weight is (downward) and (horizontally rightward).
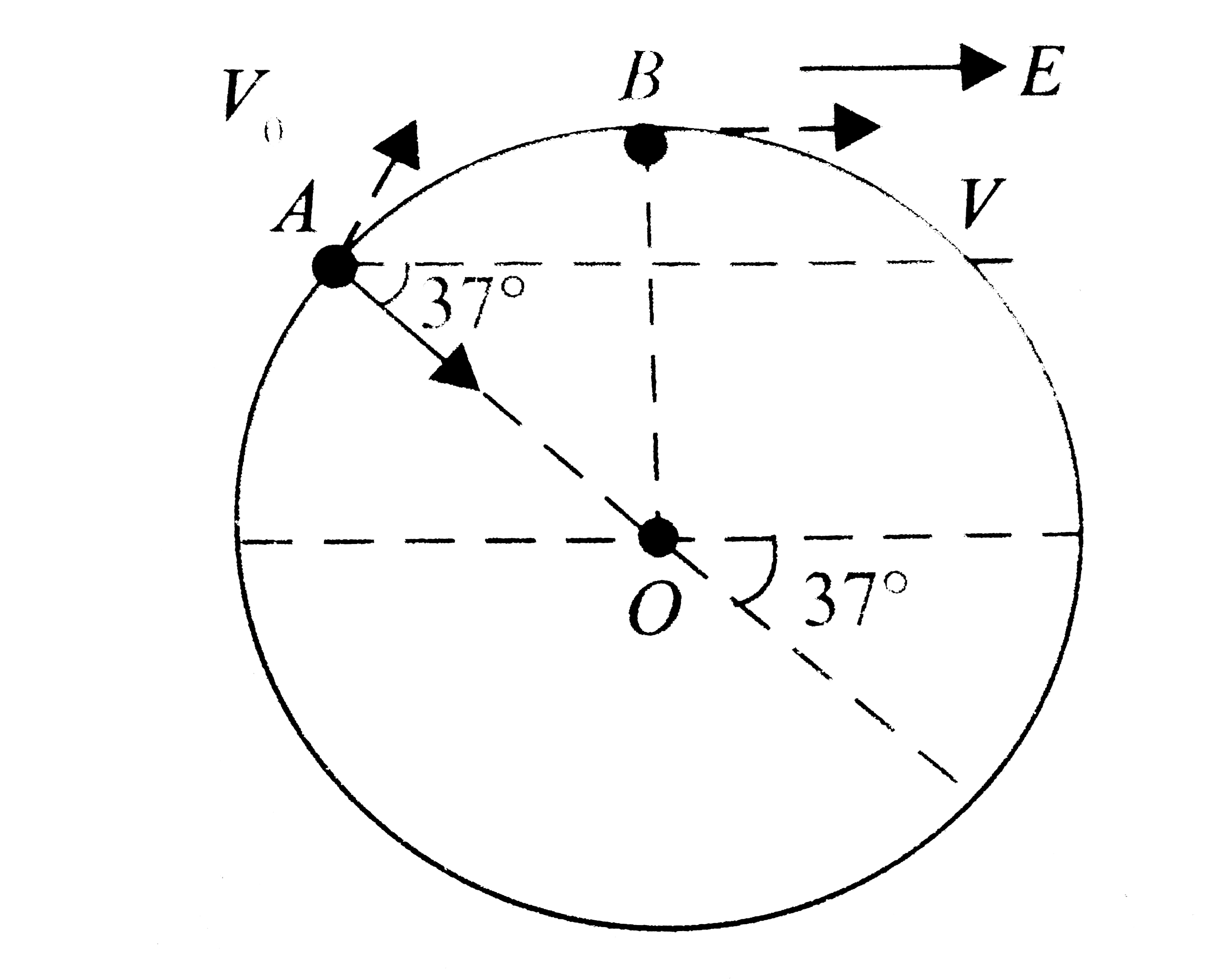
Resultant force F of these two forces is at , with the horozontal as shown in (Fig. 3.82.) Hence, tension is minimum at A, as shown in figure.
Let critical velocity at A be . Considering free body diagram of sphere at A,
or
As the sphere moves from A to B work is done on the sphere by the electric field and the gravitational potential energy increases by
We can find the required minimum velocity V, at the highest point B, by using work energy theorem between points A and B.
which gives .
 ,
,  ,
,  .
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Examples
Explore 9 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Exercise 3.1
Explore 23 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
A small sphere of mass m=0.5kg carrying a positive charge q=110μC is connected with a light, flexible, and inextensible string of length of length r=60cm and whirled in a vertical circle. If a vertically upward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
View SolutionA small sphere of mass m=0.5 kg cariying a positive charge q=110μC is connected with a light, flexible and inextensible string of length r=60 cmandwhir≤d∈avertical∘≤.Ifaverticallyupwarde≤ctriefieldofstren>hE=10^(5) N C^(-1)∃∈thespace,thentheminiμmvelocity(∈ms)ofthesphererequiredatthehighestp∮sotˆitmayjustcomp≤tethe∘≤is(g=10 ms^(-2))
View Solution
Knowledge Check
A bob of mass m = 100 gm having charge q=50μC connected with a non-conducting string of length l = 1m is whirled in vertical plane with minimum speed such that it can complete a circular path in space where electric field of strength E=2×104N/C is switched on as shown in figure. The velocity of bob at the point where tension in string become zero is
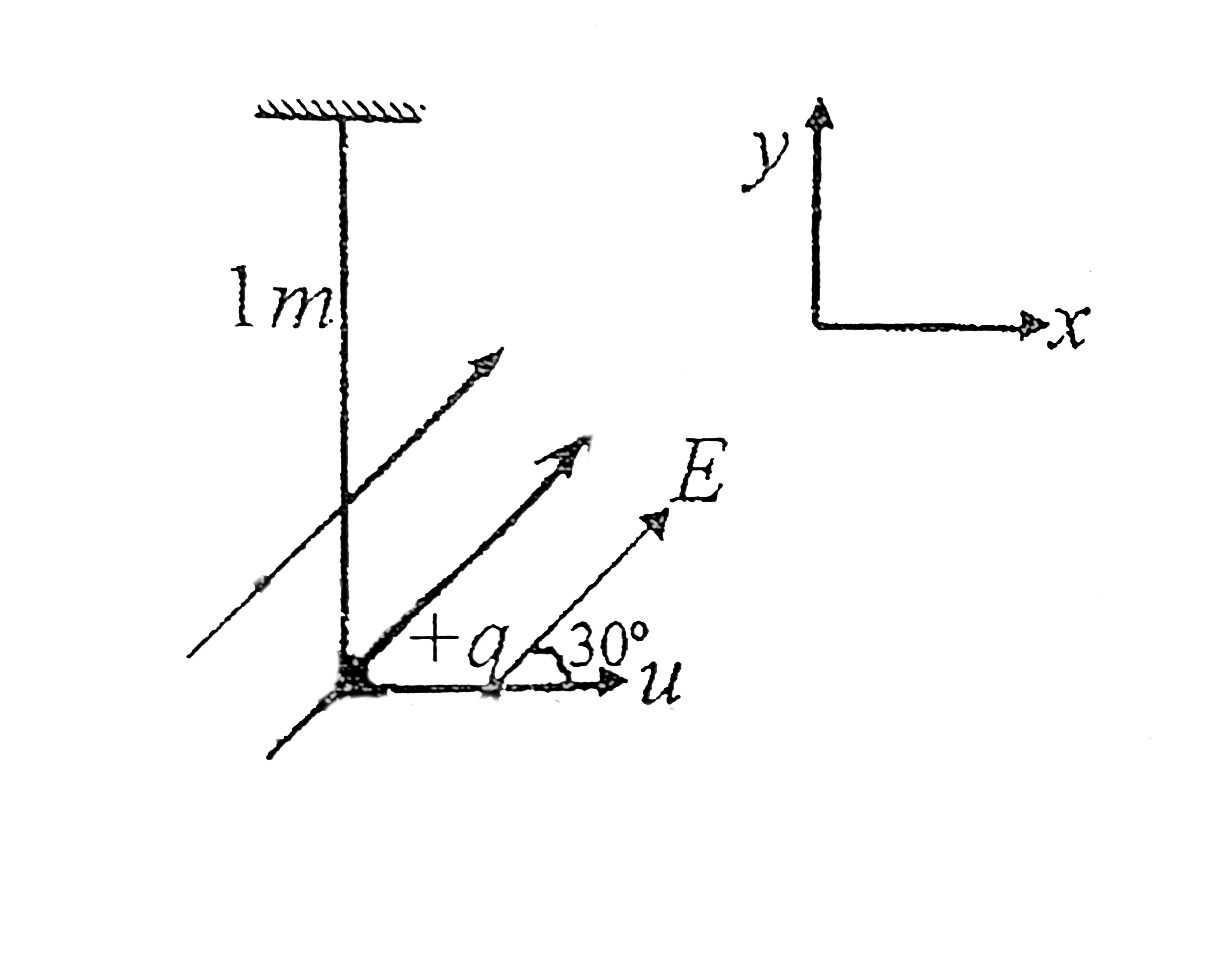 A→v=(√5ˆi+√3ˆj)B→v=√10ˆiC→v=√52(ˆi+√3ˆj)D→v=−√52(√3ˆi−ˆj)
A→v=(√5ˆi+√3ˆj)B→v=√10ˆiC→v=√52(ˆi+√3ˆj)D→v=−√52(√3ˆi−ˆj)A stone of mass 1 kg tied to a light inextensible string of length L=53m, is whirling in a vertical circle of radius L. If the ratio of the maximum and minimum tension in the string is 4 and g=10m/s2, the speed of stone at the highest point of the circle is
A5m/sB5√3m/sC5√2m/sD10m/sA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
A20m/sB10√3m/sC5√2m/sD10m/s
Two small particles A and B having masses m=0.5kg each and charges q1=(−155/18μC) and q2=(+100μC), respectively, are connected at the ends of a nonconducting, flexible, and inextensible string of length r=0.5m.
Particle A is fixed and B is whirled along a verticle circle with center at A. if a vertically ipward electric field of Strength E=1.1×105NC−1 exists in the space, calculate the minimum velocity of particle B required at the highest point so that it may just complete the circle (g=10ms−2).
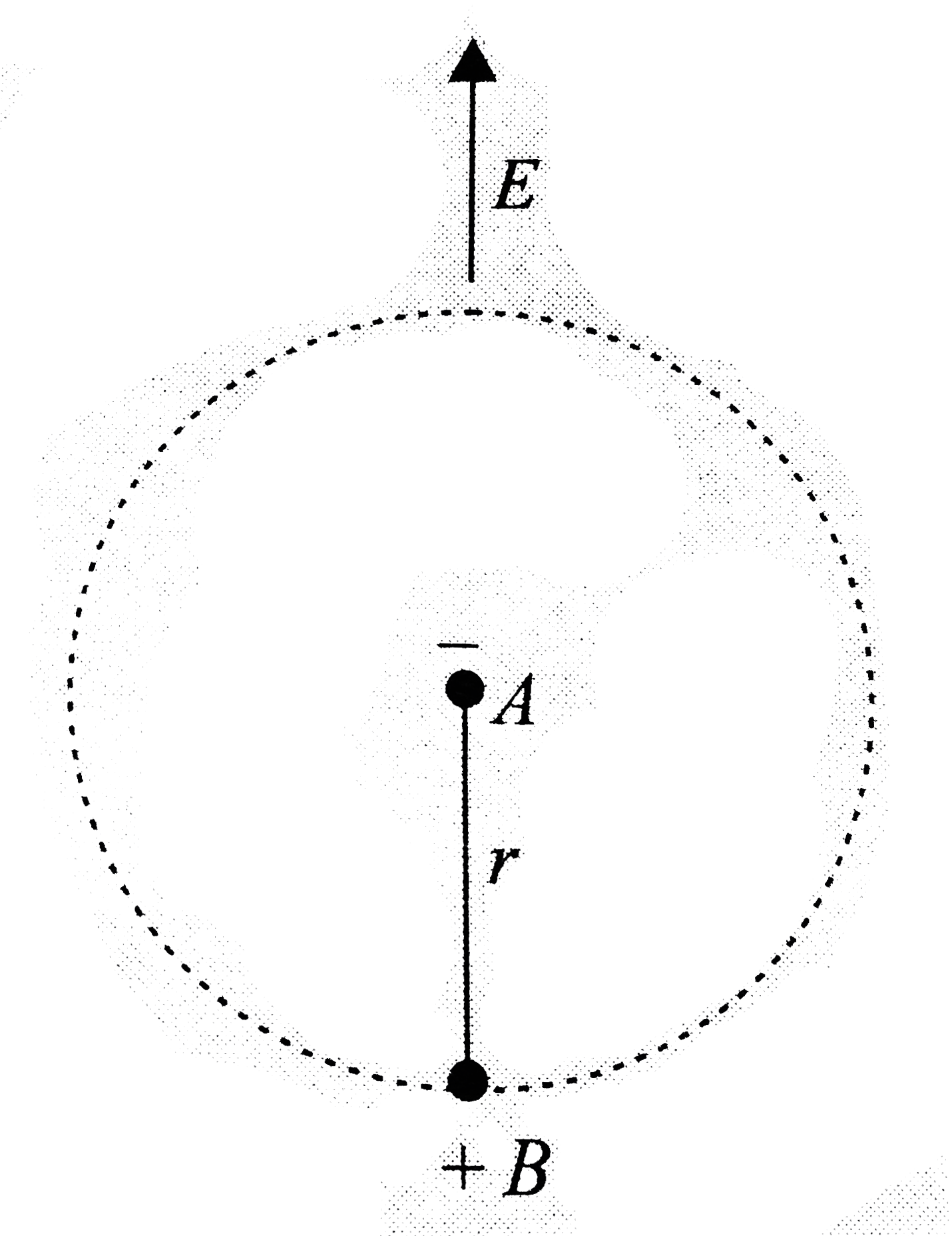 .
.
View SolutionA small sphere of mass m and carrying a charge q is attached to one end of an insulating thread of length a, the other end of which is fixed at (0,0) as showing in figure. There exists a uniform electric field →E=−→E0ˆj in the region. The minimum velocity which should be given to the sphere at (a, 0) in the direction shown so that it is able to complete the circle around the origin is (There is no gravity)
View SolutionA particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA stone of mass 100 g attached to a string of length 50 cm is whirled in a vertical circle by giving it a velocity of 7 m/s at the lowest point. Find the velocity at the highest point .
View SolutionConsider a stone of mass 1 kg tied to a light inextensible string and whirling in a vertical circular path. The length of the string is fount to be 104 m. It is also fount that theratio of the maximum to minimum tension is 3. The find the speed of the stone at the highest point of the circle in ms−1. (Take g=10ms−2)
View Solution

