A positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

Using conservation of mechanical energy ΔK+ΔU=0,
(0−12mv2)+q(Vf−Vi)=0
or 12mv2=q(Vf−Vi) ….(i)
Vi=Q4πε0randVf=q8πε0R[3−r2R2]
where r=R2,here,Vf=11Q32πε0R
Putting the values of Vi and Vf in Eq. (i)
12mv2=11qQ32πε0R−qQ4πε0r
or mv2=11qQ16πε0R−qQ2πε0r
=qQ2πε0[118R−1r]
or v2=qQ2mπε0R[118−Rr]
Hence V=√qQ2mπε0R[118−Rr].
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
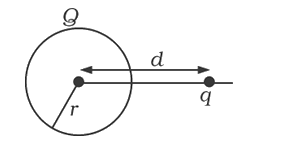
View Solution
Knowledge Check
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
AVrBR2Vr3CRVr2DrVR2A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
ARVr2BVRCrVR2DR2Vr2Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCbothDNone
A charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
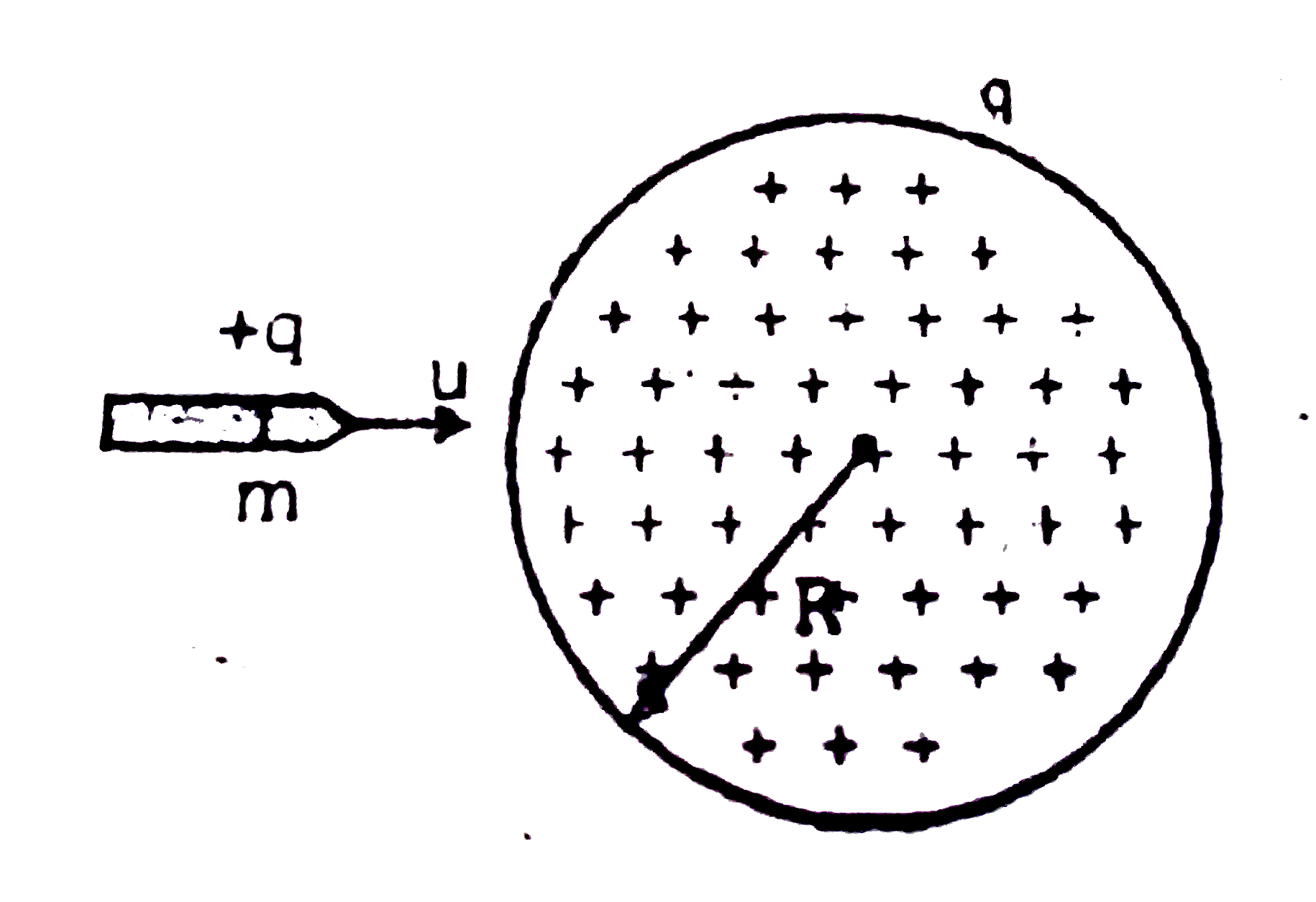
View SolutionA bullet of mass m and charge q is fired towards a solid unifromly charged sphere of redius R and total cbharge +q. If it strikes the surface of sphere with speed u, find the minimum speeed u so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrositatic forces )
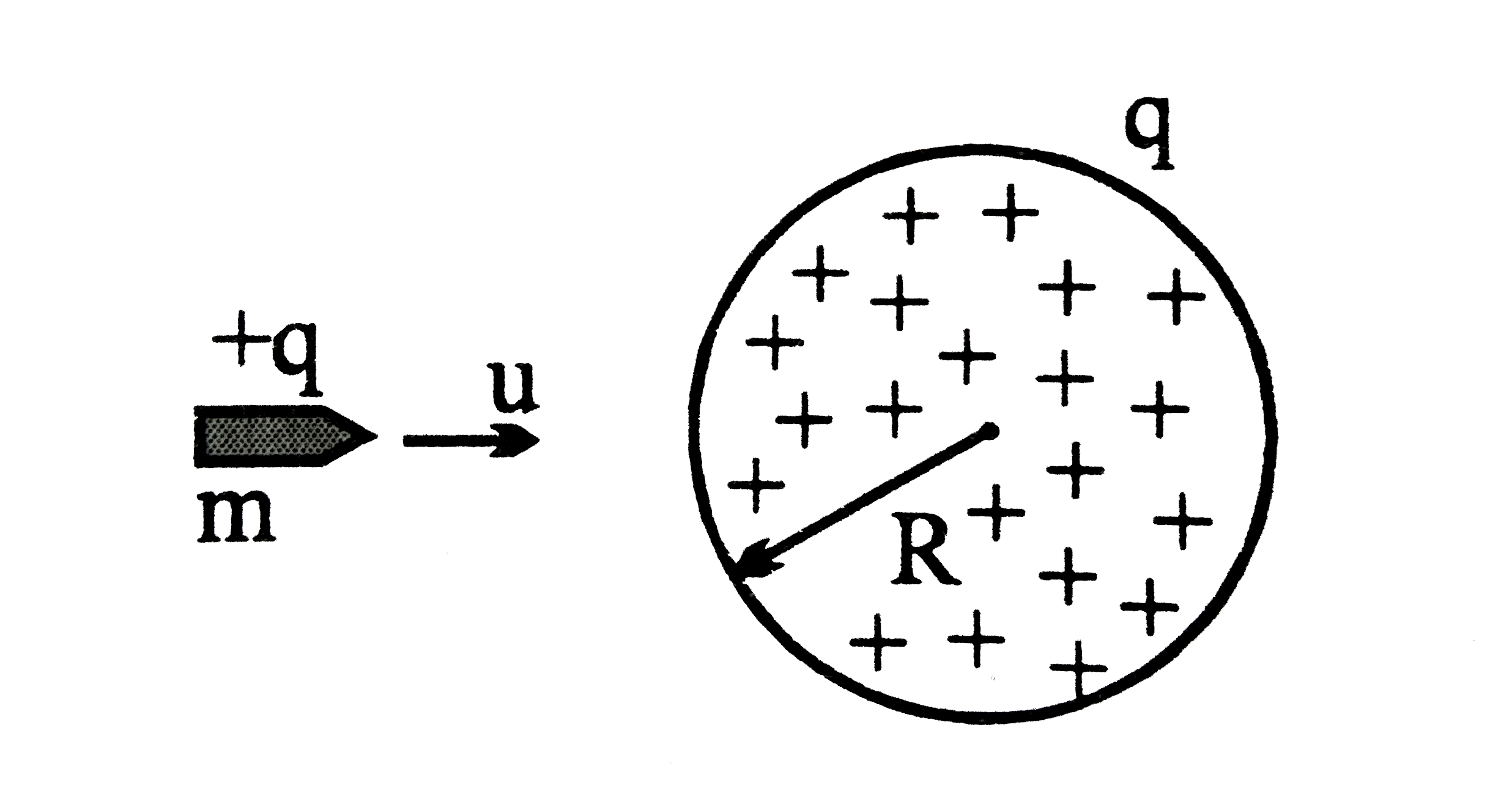 .
.
View SolutionThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
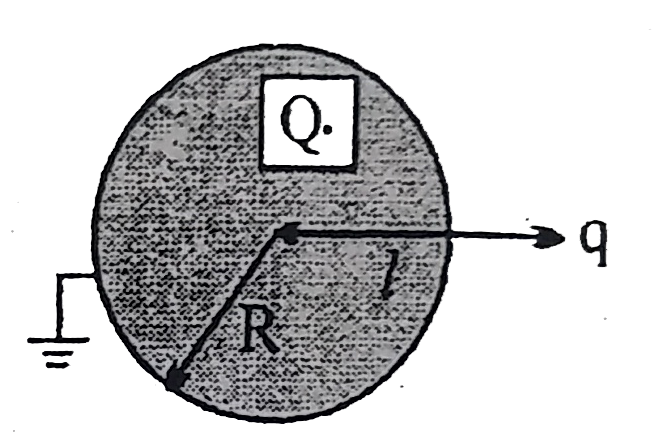
Net charge on the outer surface of conducting sphere is
View SolutionThe electric intensity of outside a charged sphere of radius R at a distance r(r>R) is
View Solution
