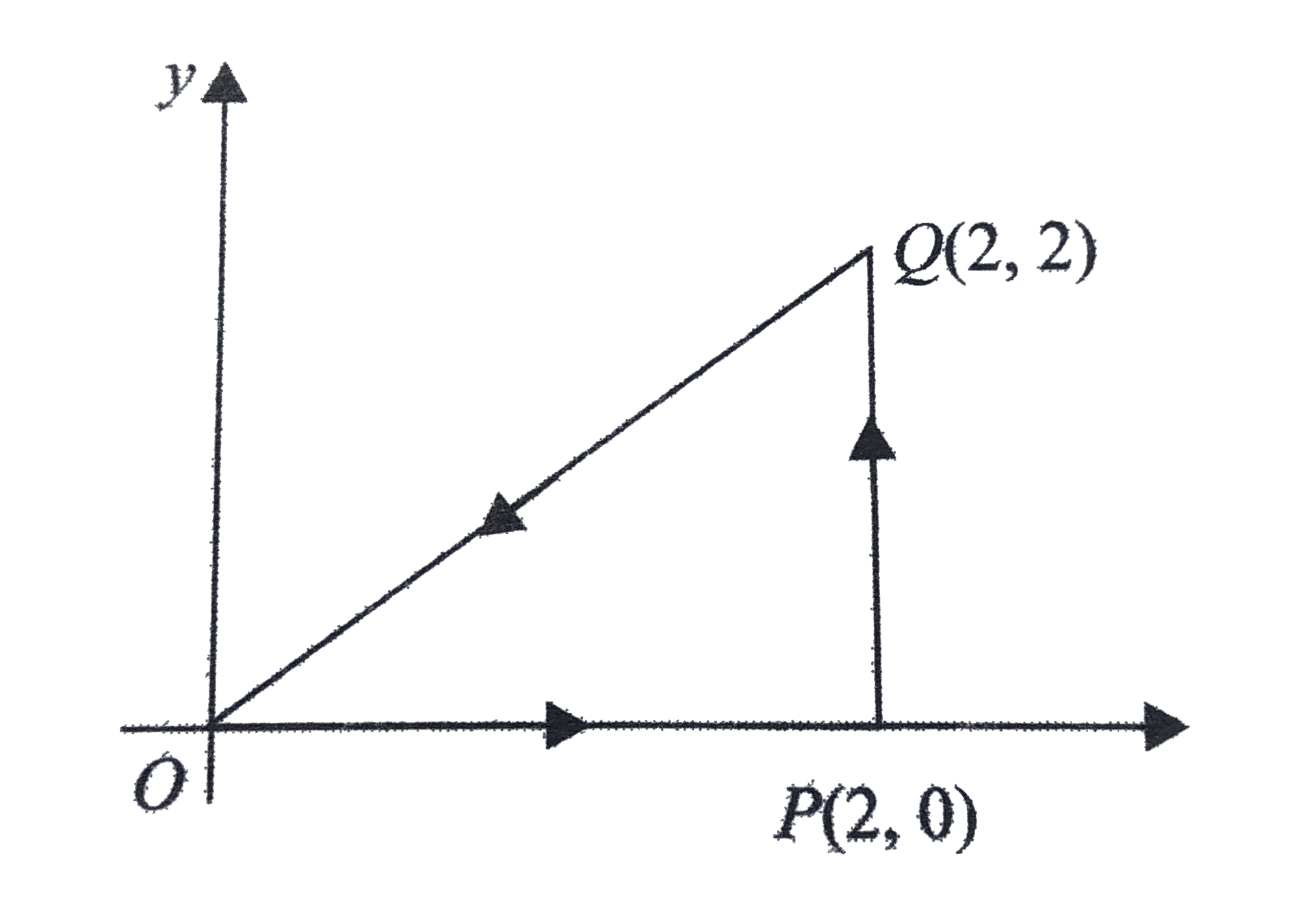
A charge particle q=−10μC is carried along OP and PQ and then back to O along QO as shown in fig. 3 . 2, in an electric field →E=(x+2y)ˆi+2xˆj Find the work done by an external agent in (i) each path and (ii) the round trip.
A charge particle q = -10 mu C is carried along OP and PQ and then back to O along QO as shown in fig. 3 . 2, in an electric field vec E = (x + 2y) hat i + 2x hat j Find the work done by an external agent in (i) each path and (ii) the round trip. ..

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(i) W=−q∫→E.d→l=−q(∫Exdx+∫Eydy)
In Path O rarr P : Since the displacement is along the x - axis for the path OP,
WO→P=−q∫Exdx=−(−10×10−6)∫20(x+2y)dx,
where y=0
or WO→P=+20×10−6J
In Path P rarr Q : Since the displacement is along y - axis for PQ,
WP→Q=−q∫Eydy=−q(2∫20xdy)
where (x = 2)
= −2(−10×10−6)∫202dy=80×10−6J
In Path Q rarr O : Since the displacement
dl=dxˆi+dyˆjalongQO,
WQ→O=−q∫(Exdx+Eydy)=−q∫02(x+2y)dx+2xdy
=−q[∫02(x+2y)dx+2∫02xdy]
where the equation of the path (QO) is given as (y = x)
or WQ→O=−q[∫02(x+2x)dx+2∫02ydy]
= −q(3x22∣∣.02+y2∣∣02)=−(−10×10−6){−3×42−4}
=−100×10−6J
(ii) Then, the total work done in the round trip is
W=WO→P+WP→Q+WQ→O=0
In the above example, ∮→E.d→l=0. Hence, the field is conservation and static.

Updated on:21/07/2023
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Charge Q is given a displacement →r=aˆi+bˆj in an electric field →E=E1ˆi+E2ˆj. The work done is.

    AQ(E1a+E2b)
    BQ√(E1a)2+(E2b)2
    CQ(E1+E2)√a2+b2
    DQ√(E21+E22)2√a2+b2

  • Find the potential V of an electrostatic field →E=a(yˆi+xˆj), where a is a constant.

    Aaxy+C
    B−axy+C
    Caxy
    D−axy

  • The potential field of an electric field →E=(yˆi+xˆj) is

    AV=−xy+constant
    BV=−(x+y)+ constant
    CV=−(x2+y2)+ constant
    DV = constant