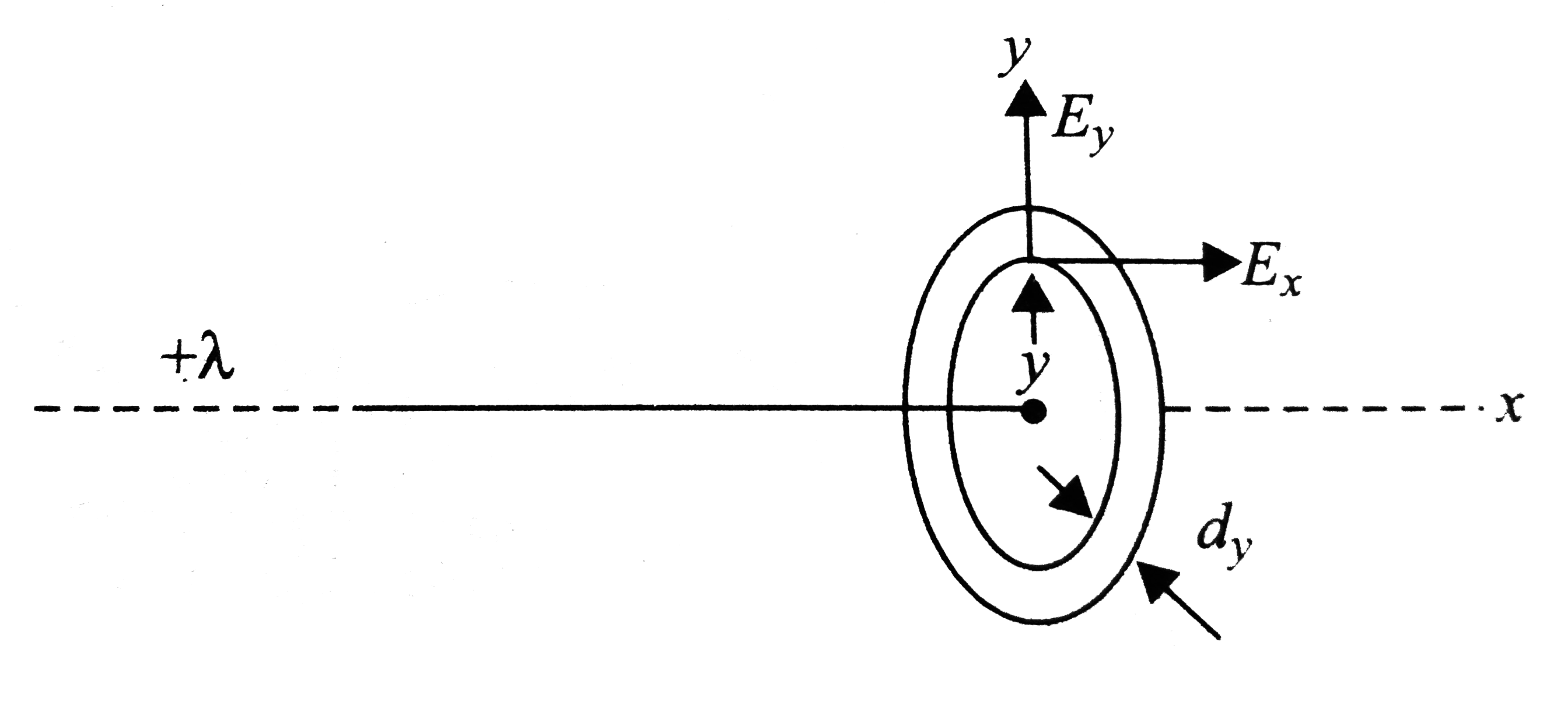
A very long uniformly charged wire oriented along the axis of a circular ring of radius R rests on its centre with one of the ends (as shown in figure). The linear charge density on the wire is . Evalute the flux of the vector across the circle area.

The correct Answer is:
The component of electric field will not contribute to flux as
angle between . Hence, flux due to is
or
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Single Correct
40 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.2
14 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
A very long uniformly charge thred oriented along the axis of a circle of radius R=1m rests on its centre with one of the ends. The charge per unit length on the thread is λ=16ε0. Find the flux of the vector E through the circle area in (Vm).
View SolutionA very long uniformly thread oriented along the axis of a a circle of raius R rests on its centre with one of the ends. The charge of the thread per unit length is equla to λ. Find the flux of the vector E across the circle area.
View Solution
Knowledge Check
If linear charge density of a wire as shown in the figure is λ
 Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the aboveA positive charge Q is uniformly distrubuted along a circular ring of radius R.a small test chage q is placed at the centre of the ring .The
 Aif q>0 and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.Bif q<0 and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.Cif q<0 it will perform SHM for small displacement along the axisDq at the centre of the ring is in an unstable equilibrium within the plane of the ring for q<0
Aif q>0 and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.Bif q<0 and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.Cif q<0 it will perform SHM for small displacement along the axisDq at the centre of the ring is in an unstable equilibrium within the plane of the ring for q<0A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
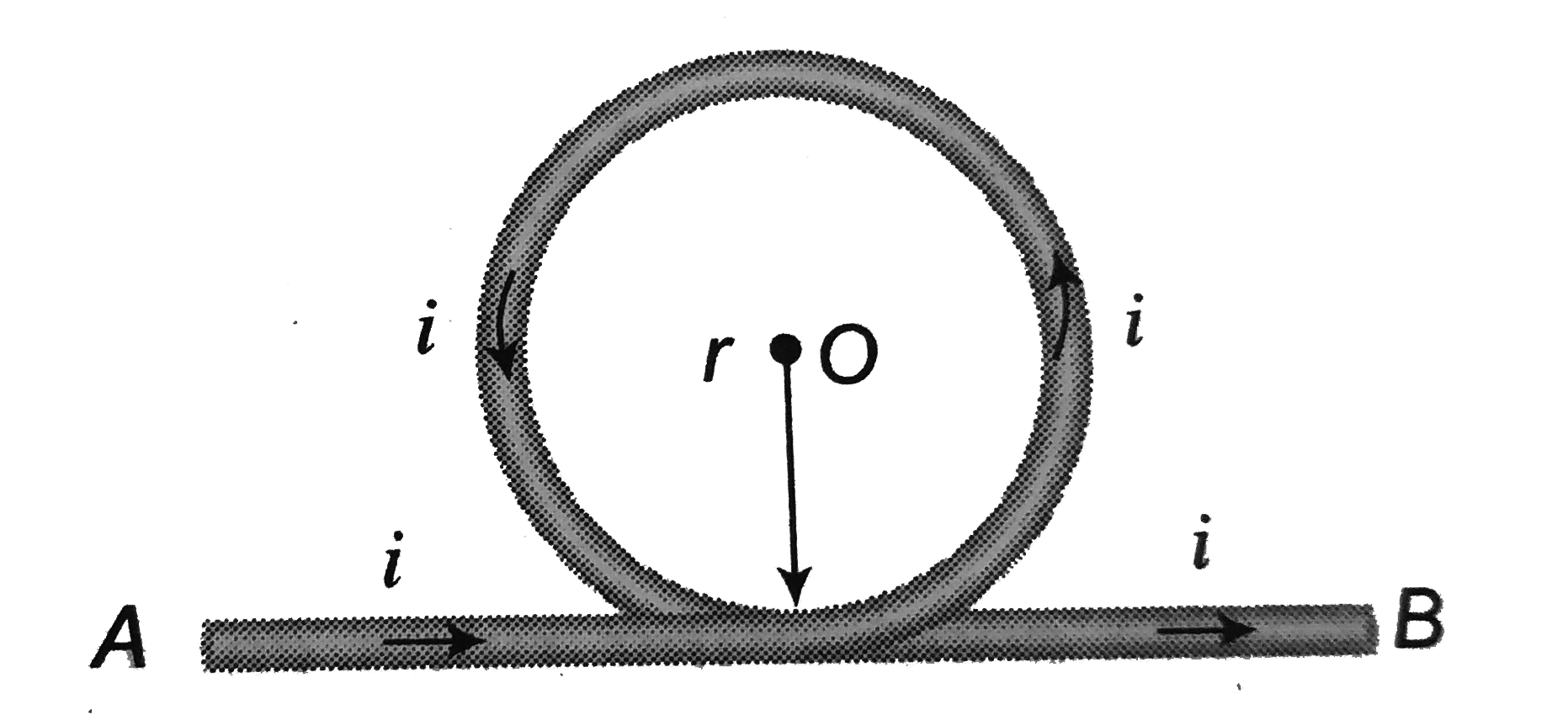 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
A system consits fo a thin charged wire ring of radius R and a very long uniformly charged thread oriented along the axis of the ring, with one of its ends coinciding with the centre of the ring. The total charge of the ring, with one of the ring so equal to q. The charge of the thread (per unit length) is equal to λ. Find the interaction froce between the ring and the thread.
View SolutionA short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

View SolutionA very long charged wire (lying in the xy plane ) which is having a linear charge density λ is having one of its end at a point P as shown in figure . What is electric field intensity at point Q :
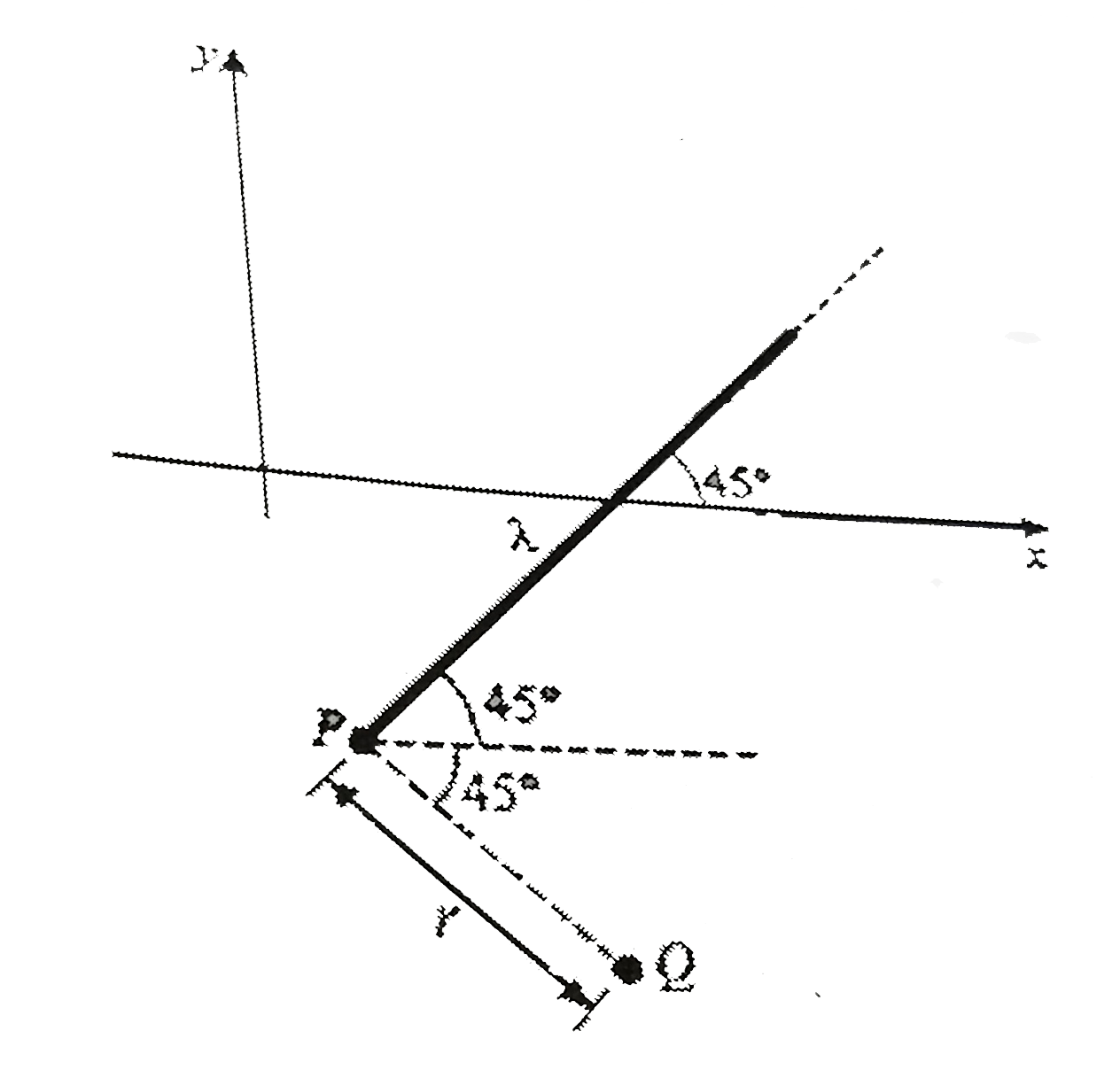
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View Solution
