The area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
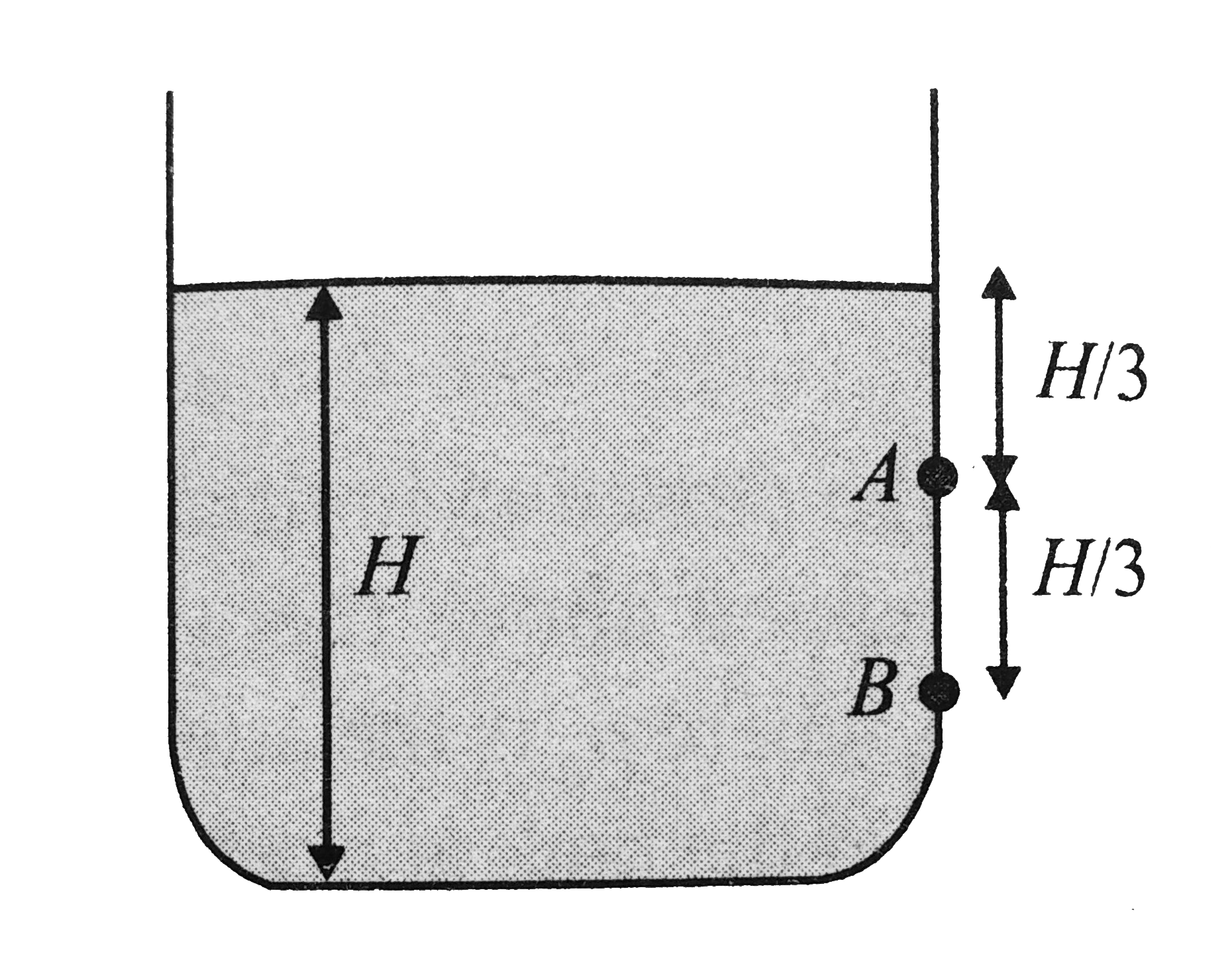
The velocity of efflux at hole B is 2 times the velocity of efflux at hole A.
The velocity of efflux at hole B is √2 time the velocity of efflux at hole A.
The discharge is same through both the holes.
The discharge through hole A is √2 time the discharge through hole B.
The correct Answer is:B, D
VA=(2gH3)12
VB=(4gH3)=√2(2gH3)12=√2VA
QA=VA(2a)
and QB=VB(a)=VA√2(a)QAQB=√2
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Linked Comprehension
Explore 43 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A squre hole of side length l is made at a depth of h and a circular hole is made at a depht of 4 h from the surface of water in a water tank kept on a horizontal surface (where l ltlt h). Find the radius r of the circular hole if equal amount of water comes out of the vessel through the holes per second.
View SolutionEqual volumes of two immiscible liquids of densities ρ and 3ρ are filled in a big vessel. Two small holes are punched at depth h/3 and 4h/3 from upper surface of lighter liquid. If v1 and v2 are velocities of efflux at these two holes, then v1/v2 is

View Solution
Knowledge Check
Two holes 1 and 2 are made at depths h and 16h reapectively. Both the holes are circular but radius of hole-1 is two times.
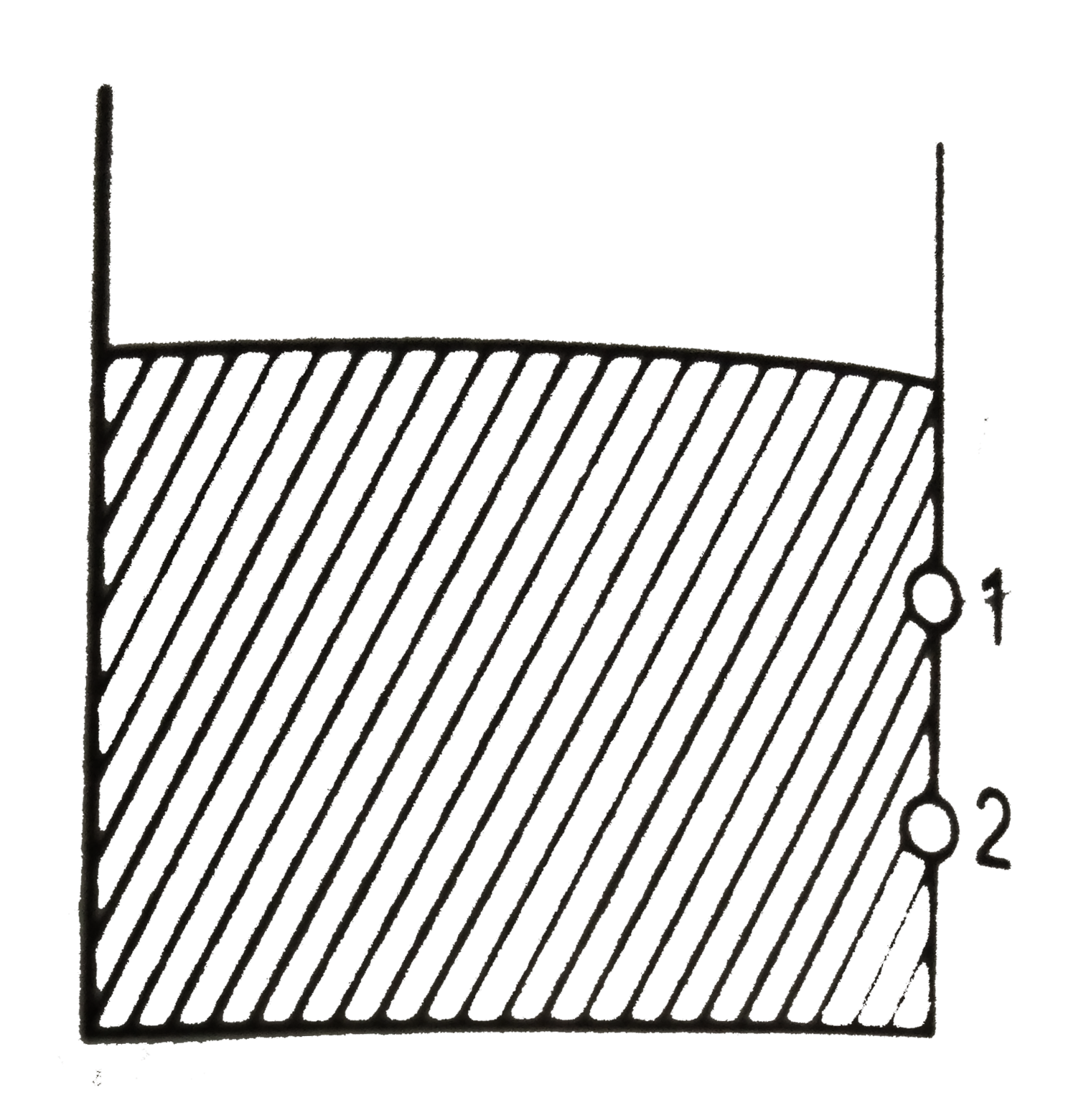 AInitially equal volumes of liquid will flow from both the holes in unit timeBIntially more volume of liquid will flow from hole-2 per unit time.CAfer some time more volume of liquid will flow from hole-1 per unit time.DAfter some time more volume of liquid will flow from hole-2 per unit time
AInitially equal volumes of liquid will flow from both the holes in unit timeBIntially more volume of liquid will flow from hole-2 per unit time.CAfer some time more volume of liquid will flow from hole-1 per unit time.DAfter some time more volume of liquid will flow from hole-2 per unit timeA large open tank has two holes in the wall. The top hole is a square hole of side L at a depth y from the surface of water. The bottom hole is a circular hole of radius R at a depth 4y from surface of water . If R=L/2√π, find the correct graph. V1 and V2 are the velocities in top and bottom holes. Area of the square & curcular holes are a1 and a2
A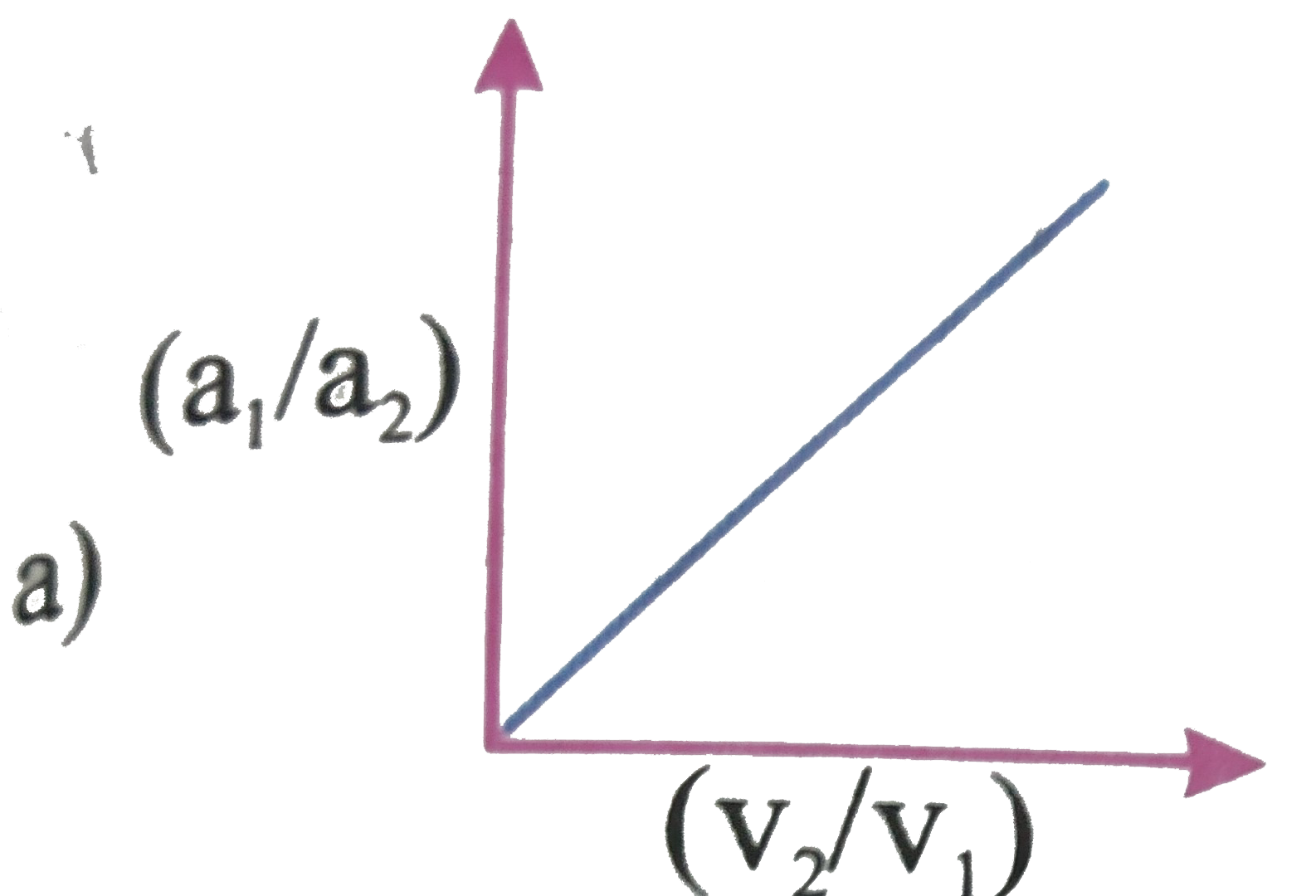 B
B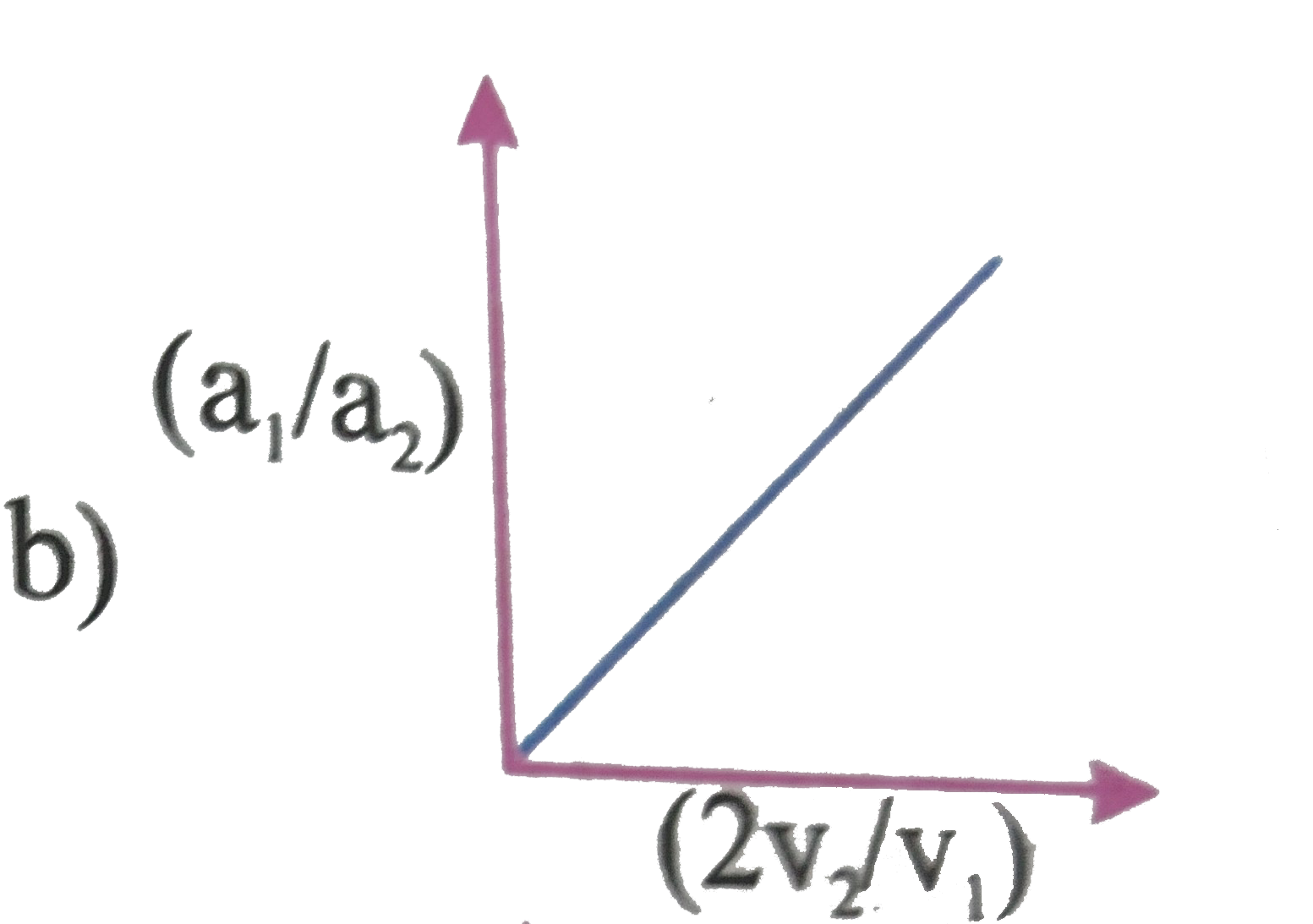 C
C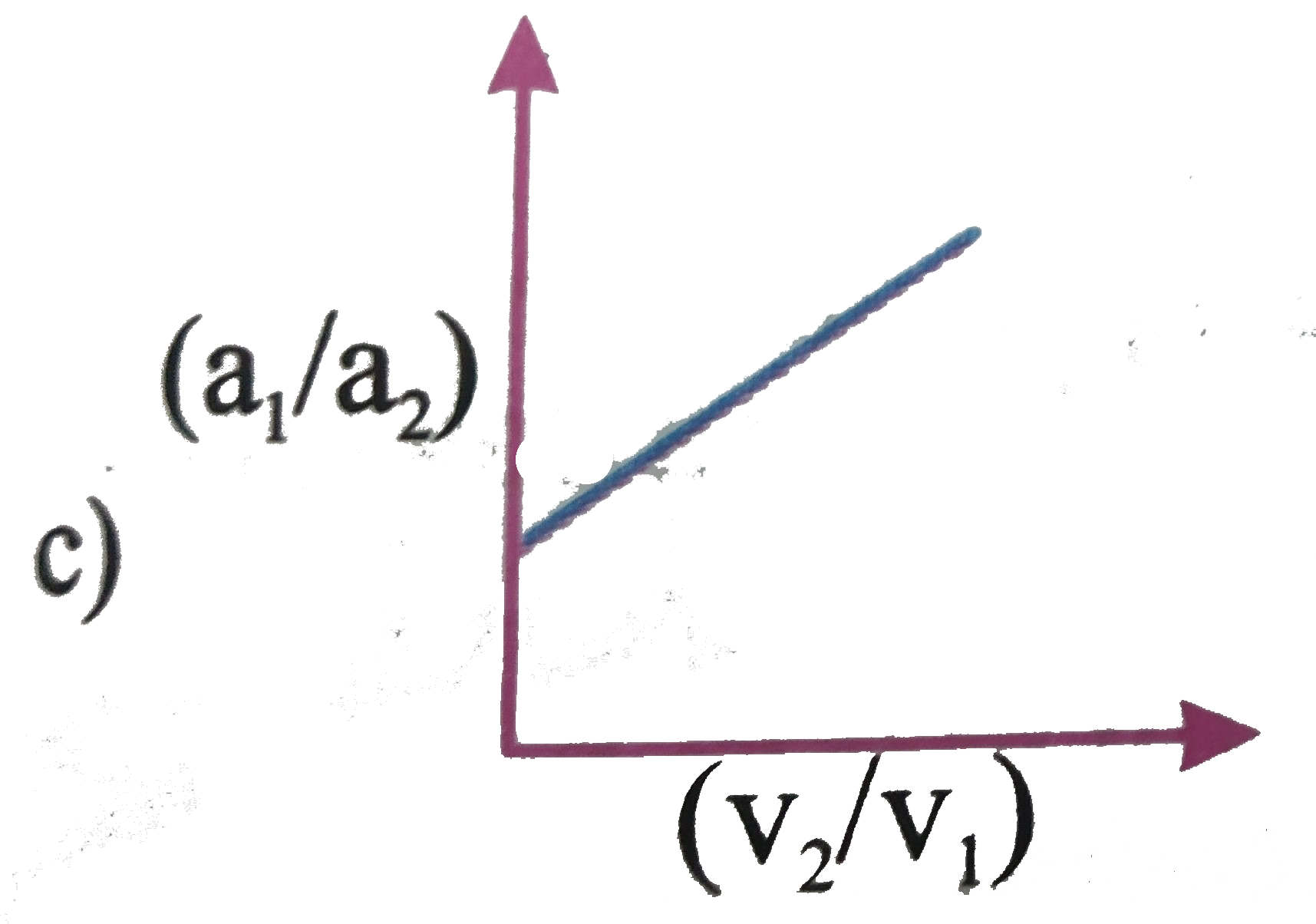 D
D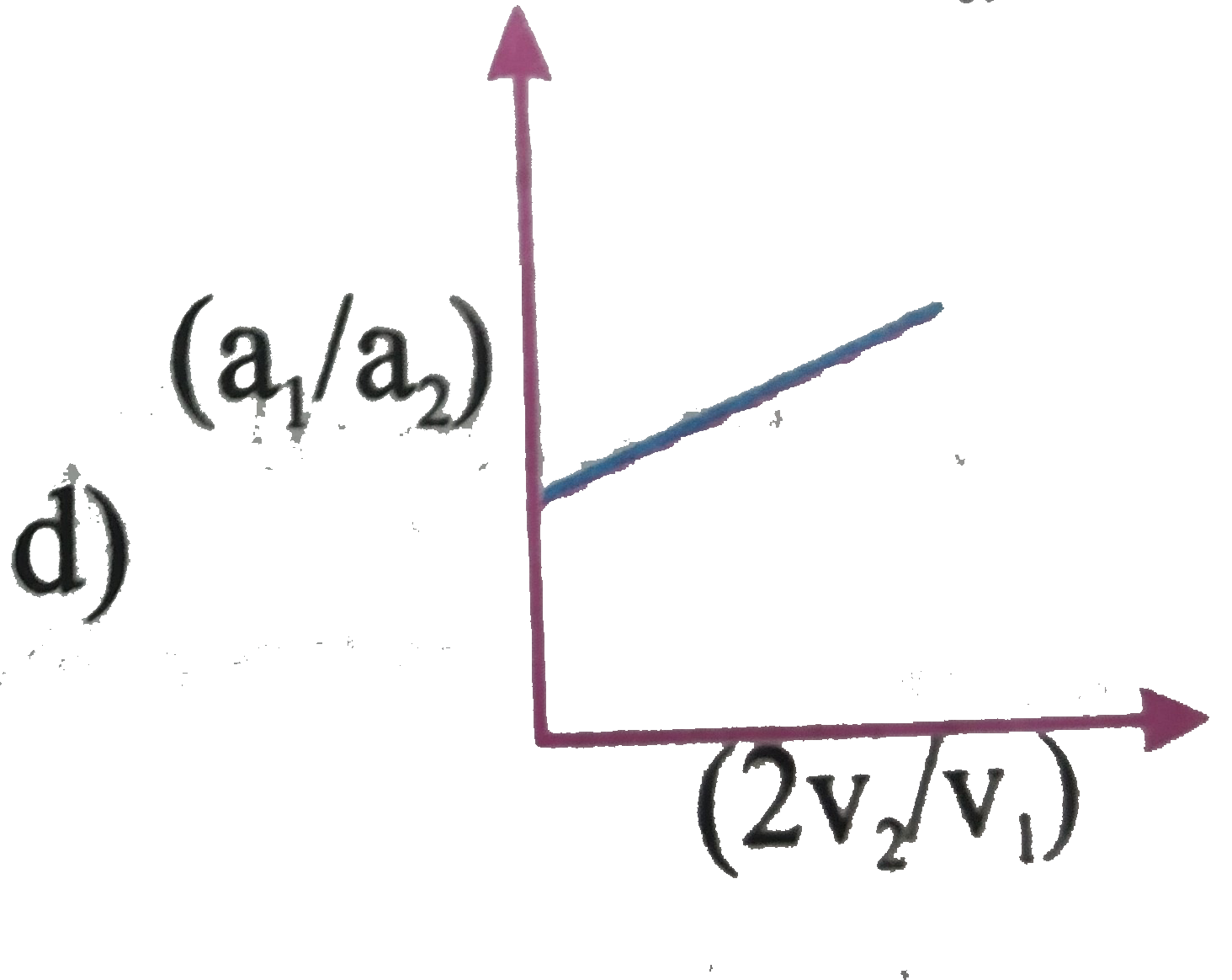
Equal volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
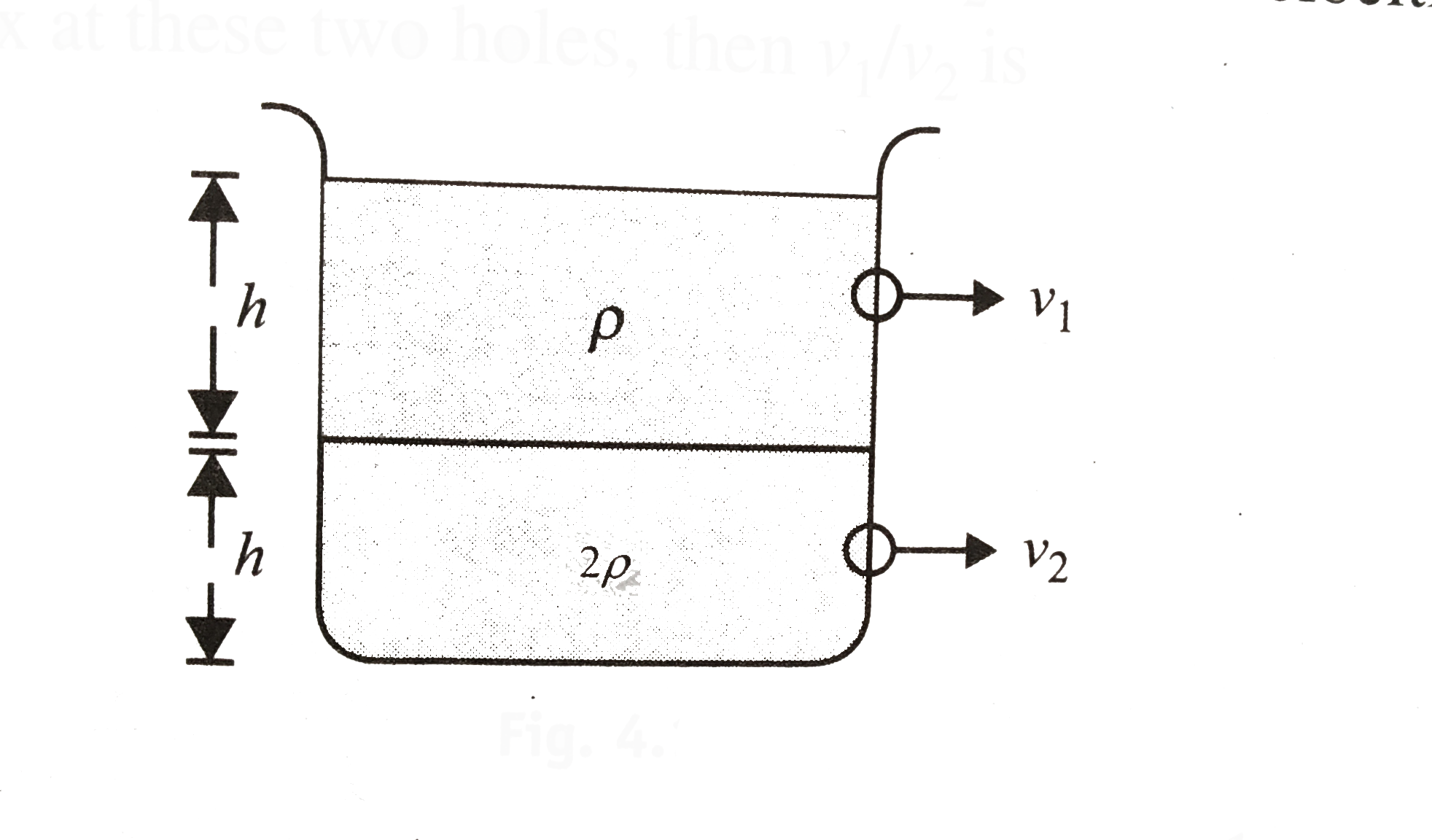 A12√2B12C14D1√2
A12√2B12C14D1√2
Equal volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is

View SolutionIn a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is

View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View SolutionIn a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is

View Solution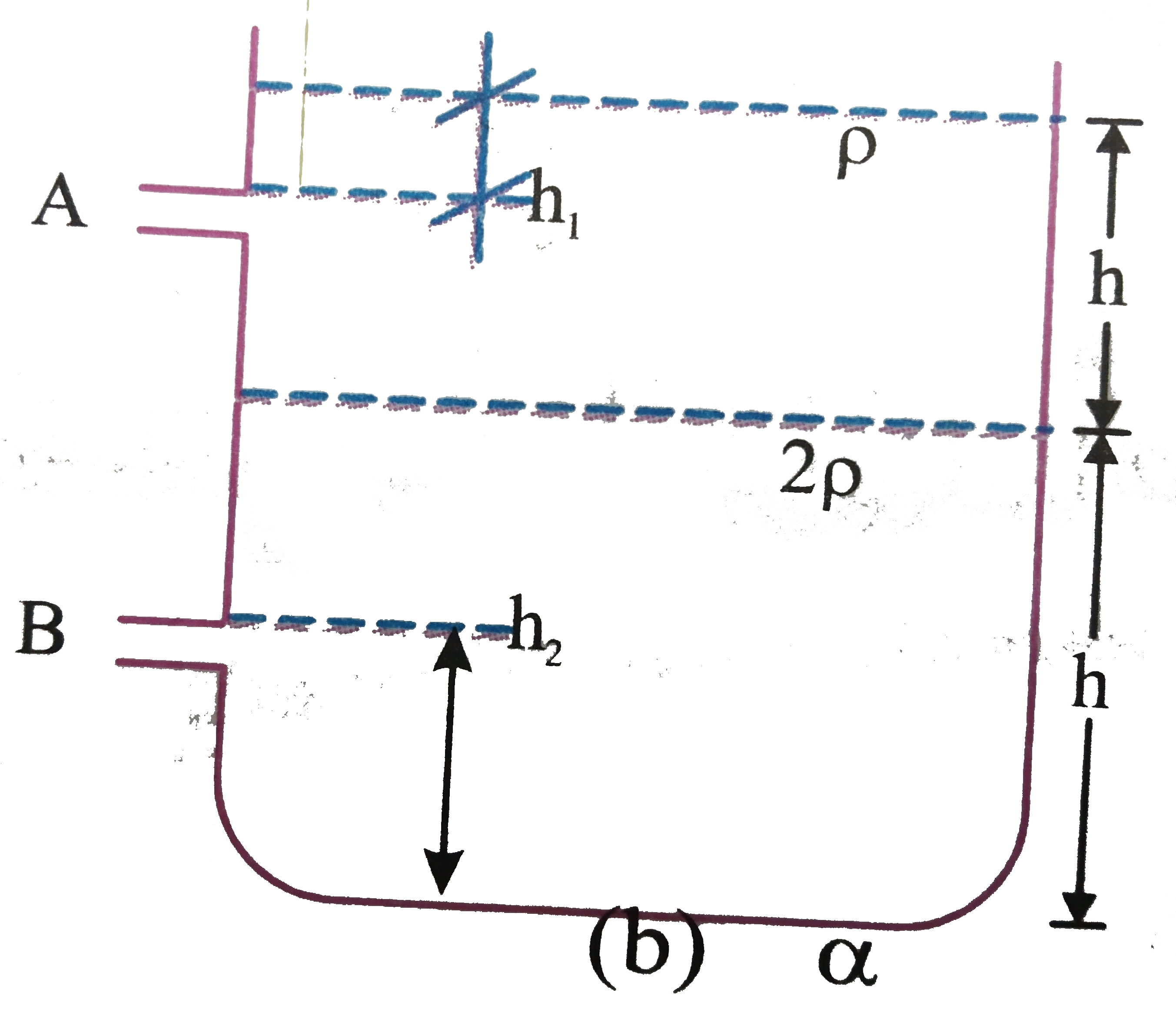
In the arrangement shown two liquids of density ρ and 2ρ are filled in a container the height of both liquids is h. there are two holes A and B at heights h1 and h2 from top liquid surface and bottom of the vessel. if V1 and V2 are the velocities of efflux at the two holes A and B respectively, find the correct graph.
Take =α(V2V1)2
View Solution

