Two holes 1 and 2 are made at depths h and 16h reapectively. Both the holes are circular but radius of hole-1 is two times.
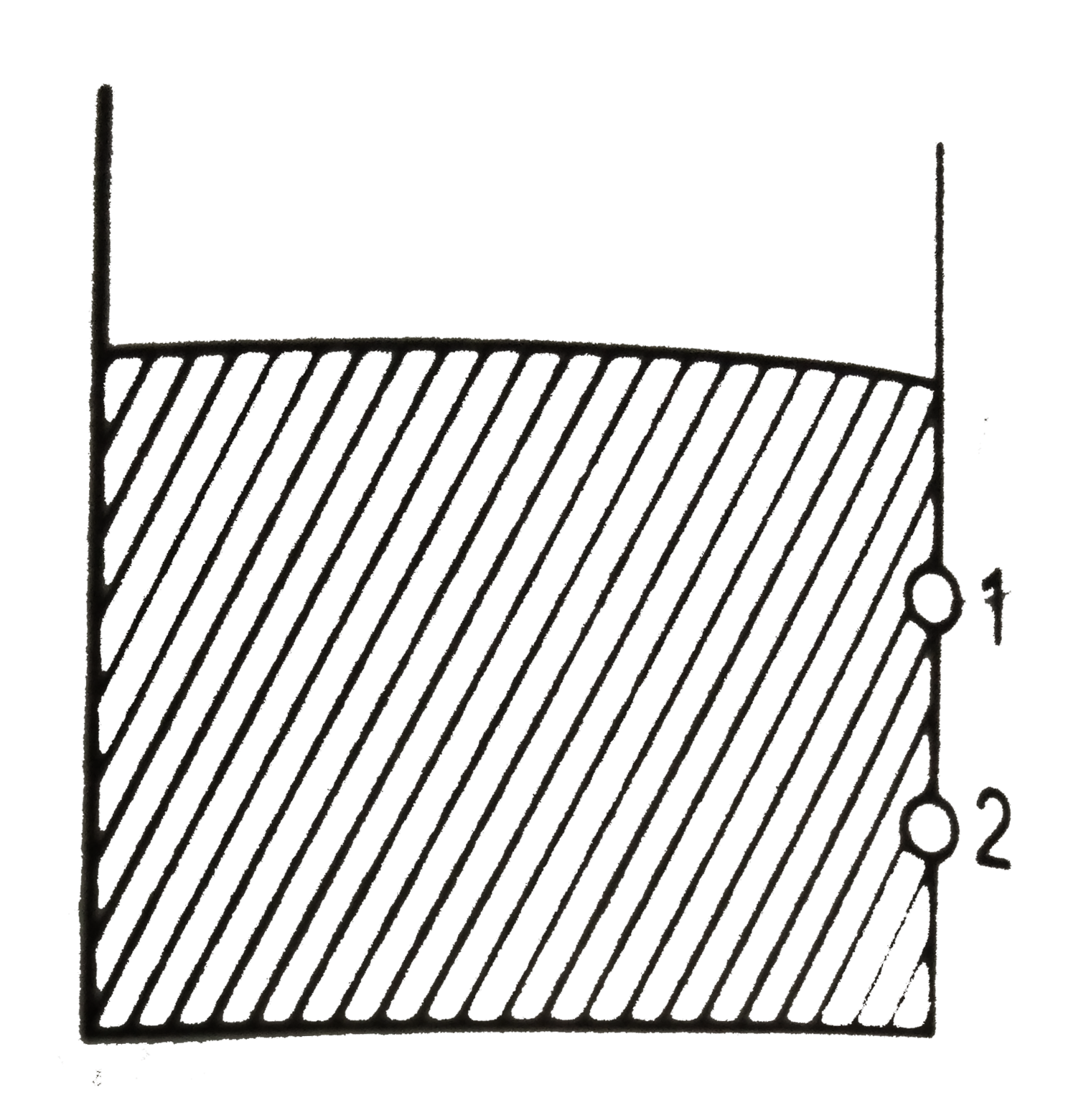
Initially equal volumes of liquid will flow from both the holes in unit time
Intially more volume of liquid will flow from hole-2 per unit time.
Afer some time more volume of liquid will flow from hole-1 per unit time.
After some time more volume of liquid will flow from hole-2 per unit time
The correct Answer is:A, D
Initially
dV1dt=v1a1=(√2gh)(π)(2R)2 …(i)
dV2dt=v1a1=(√2gh(16h))(π)(R)2 …(ii)
From Eqs, (i) and (ii) we can see that
dV1dt=dV2dt
After some time v1 both will decrease, but decrease in the value of v1 is more dominating so,
a1v1 or dV1dt,<a2v2 or dV2dt.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Level 2 Comprehension Based
Explore 7 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Subjective
Explore 24 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Level 2 Single Correct
Explore 36 Videos
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
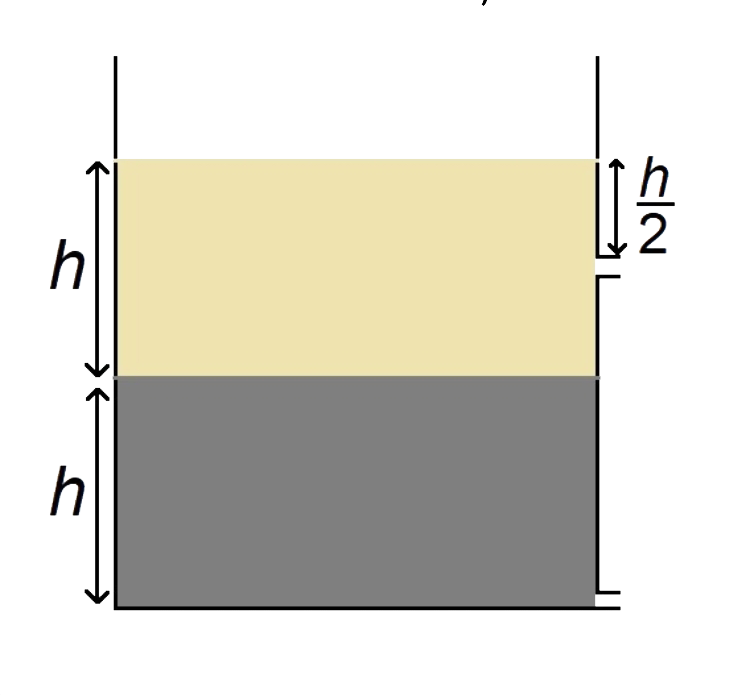
Equal volumes of two immiscible liquids of density 2ρand4ρ , respectively , are filled in the vessel as shown in the figure. Two small holes are punched at depth h2and2h, respectively , from the surface of the lighter liquid. If v1andv2 are the velocities of efflux at these holes, then the ratio of v1v2 is
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth h from the top and the other is a circular hole of radius r at a depth 4h from the top. Whwn the tank is completely filled with water, the quantity of water flowing out per second from both the holes are the same. What is the value of r?
View Solution
Knowledge Check
The area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
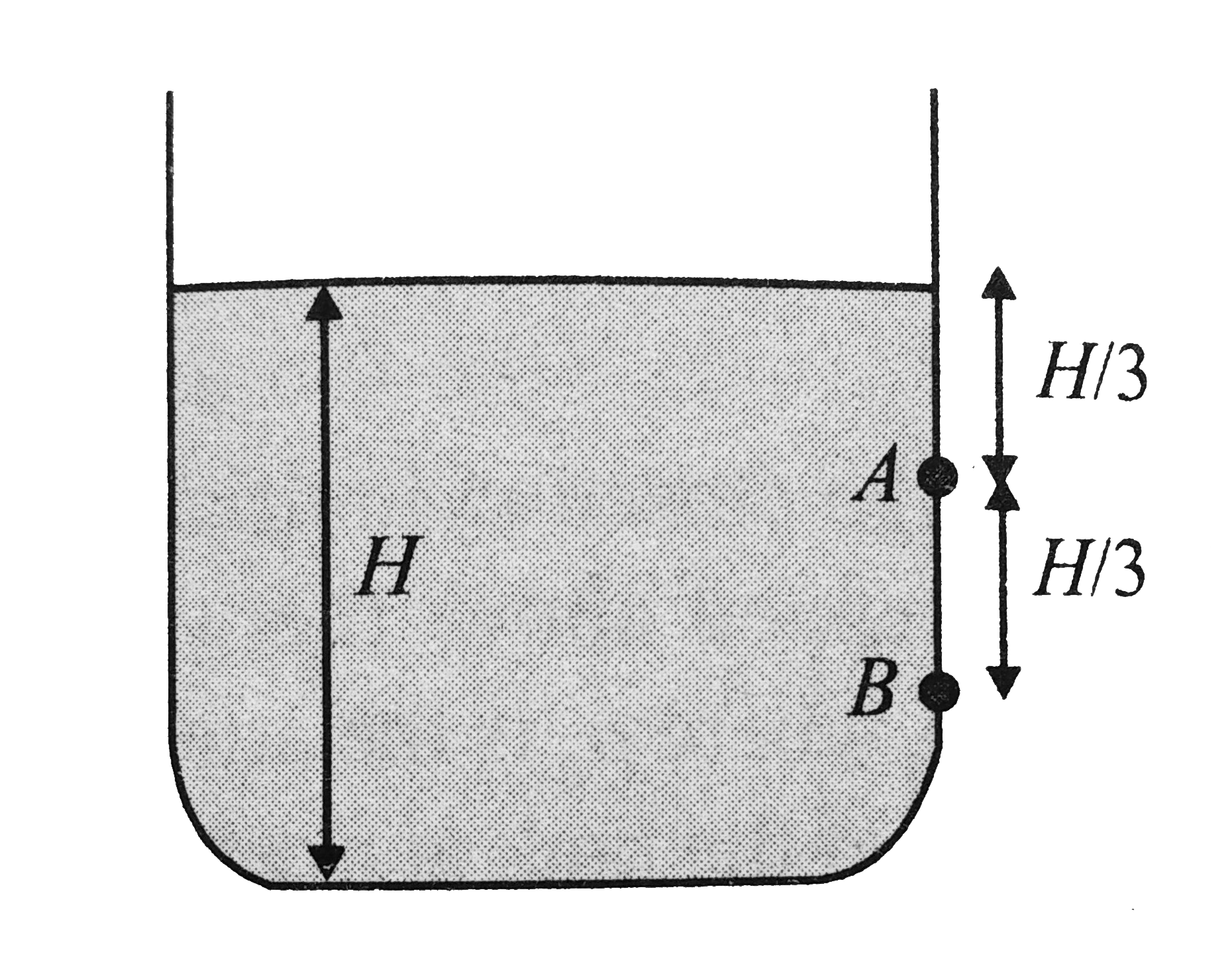 AThe velocity of efflux at hole B is 2 times the velocity of efflux at hole A.BThe velocity of efflux at hole B is √2 time the velocity of efflux at hole A.CThe discharge is same through both the holes.DThe discharge through hole A is √2 time the discharge through hole B.
AThe velocity of efflux at hole B is 2 times the velocity of efflux at hole A.BThe velocity of efflux at hole B is √2 time the velocity of efflux at hole A.CThe discharge is same through both the holes.DThe discharge through hole A is √2 time the discharge through hole B.A large open tank has two holes in the wall. The top hole is a square hole of side L at a depth y from the surface of water. The bottom hole is a circular hole of radius R at a depth 4y from surface of water . If R=L/2√π, find the correct graph. V1 and V2 are the velocities in top and bottom holes. Area of the square & curcular holes are a1 and a2
A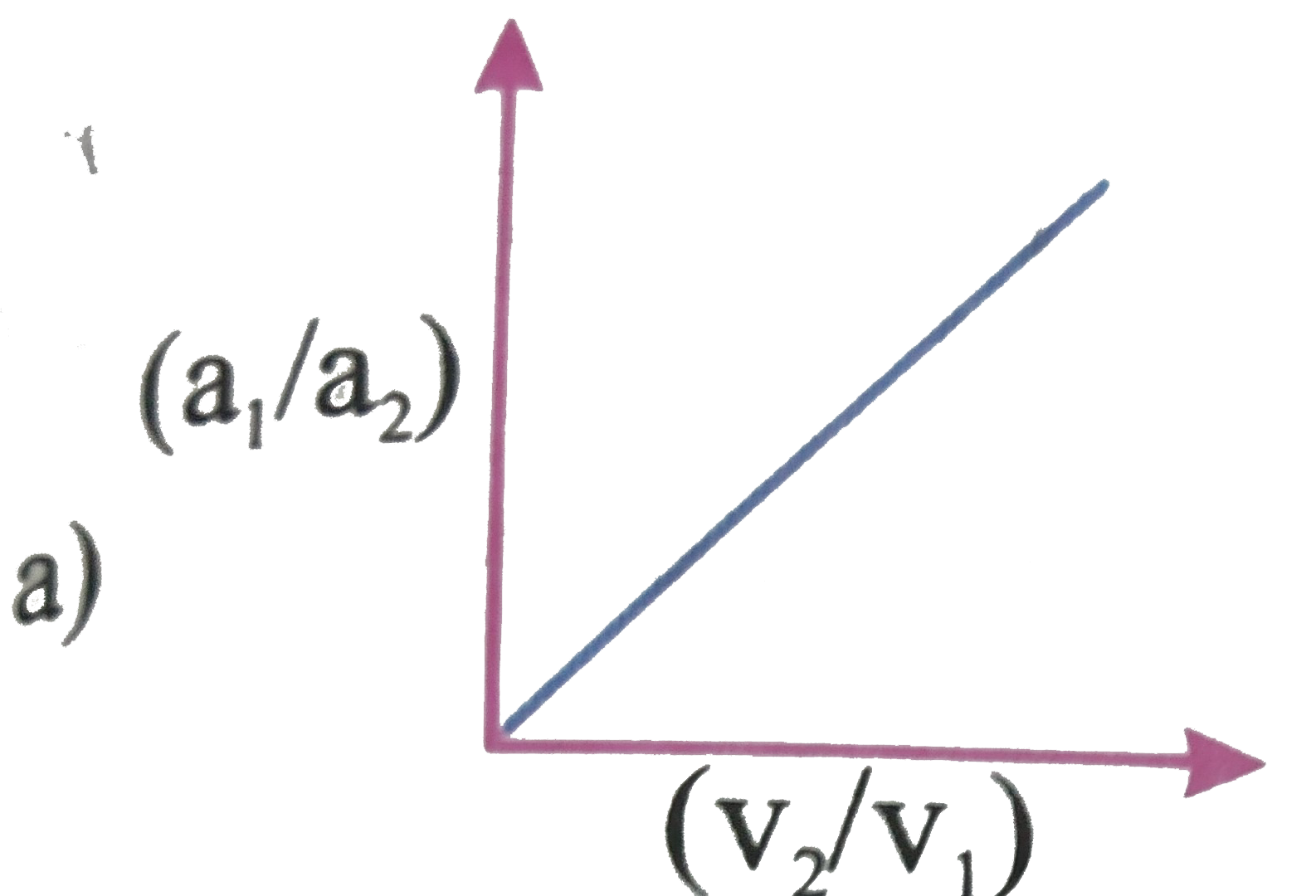 B
B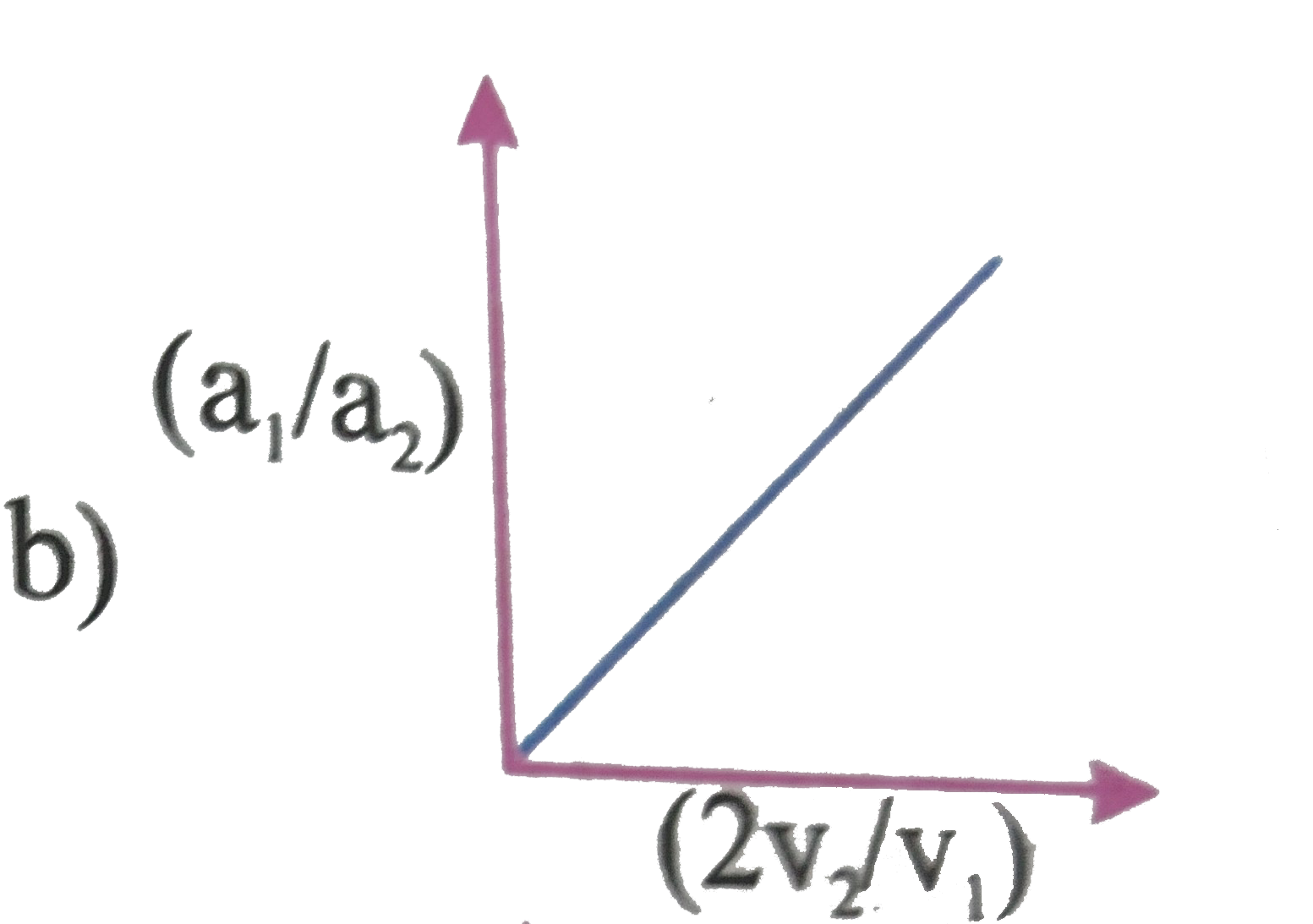 C
C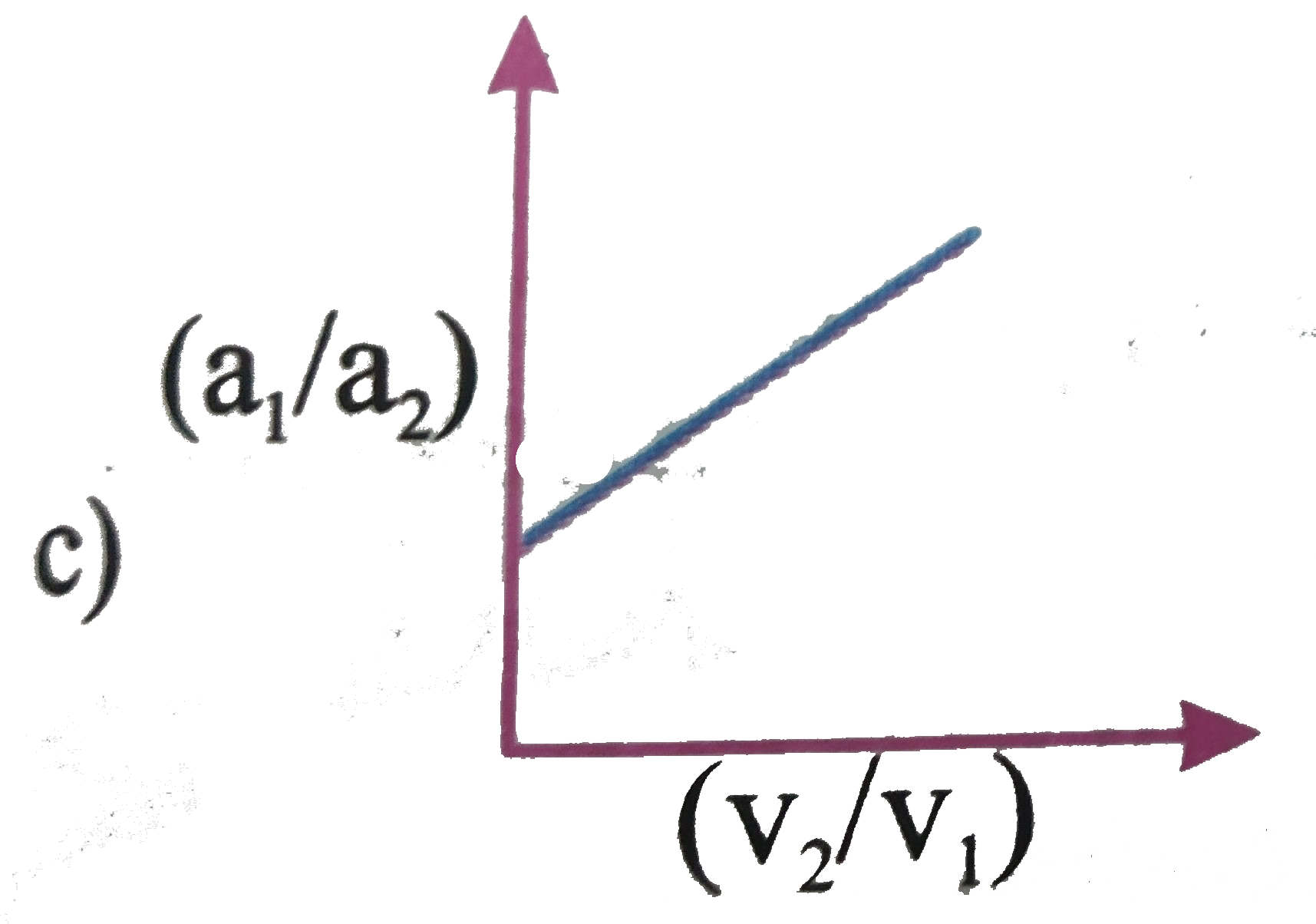 D
D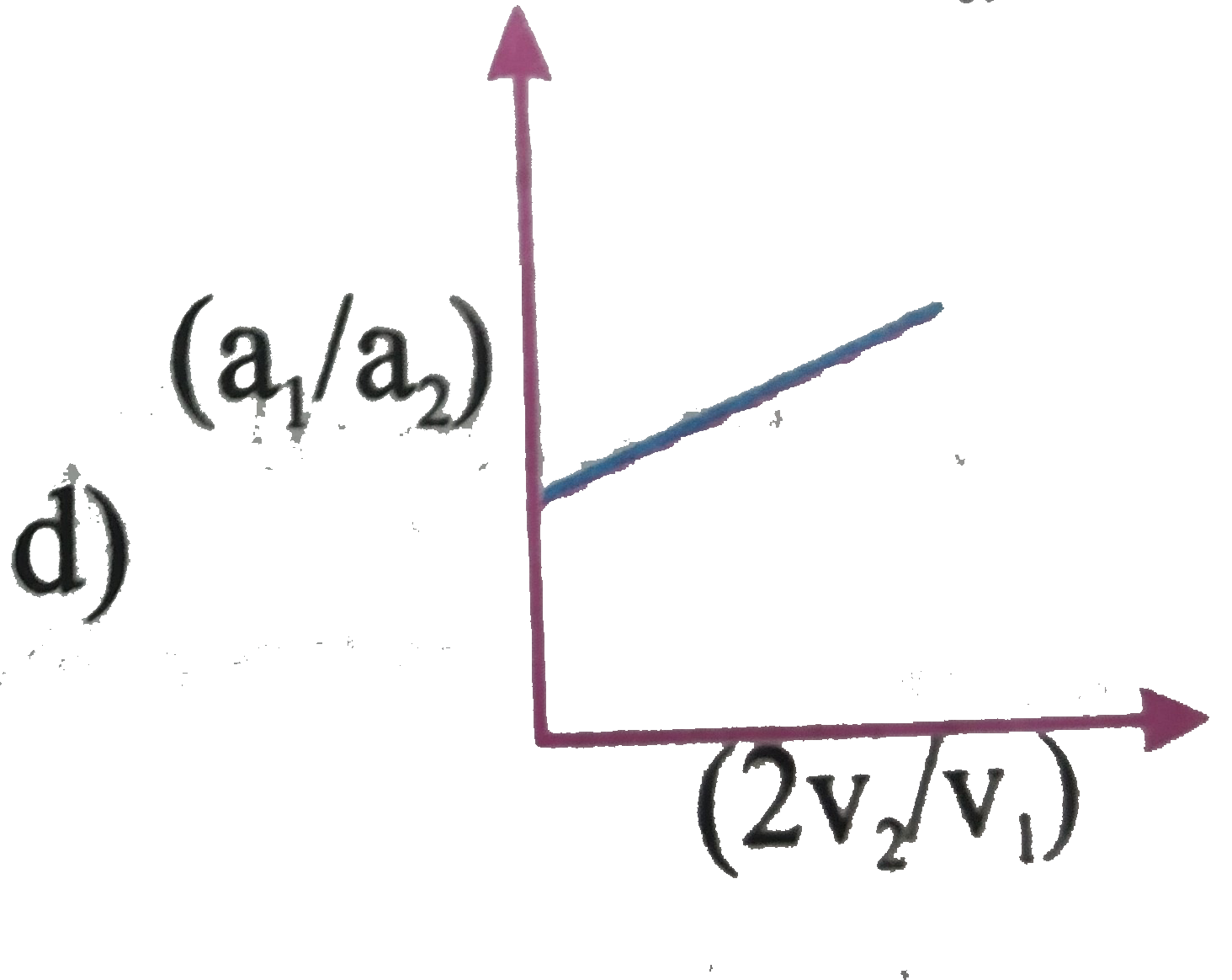
In a cylindrical vessel containing liquid of density ρ, there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole, for which the range of efflux would be maximum, will be –
 Ah2−H1BH2+H2C⋅h2−h2)2Dh2+h12
Ah2−H1BH2+H2C⋅h2−h2)2Dh2+h12
Two holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

The ratio v1v2 will be
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increased
View SolutionIn a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View Solution