A U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
Let ymax be the lowest point on the dotted parabola show in figure.
y1=r21ω22g+ymin and y2=r22ω22g+ymin
∴h=y2−y1=(r22−r21)ω22g=ω22g(r22=r21)

Alternatively, we may apply Bernoulli's equation between point A and B
Patm+12ρ(r1ω)2=Patm+12ρ(r2ω)2=ρgh
⇒h=(r22−r212g)ω2
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Solved Examples
Explore 7 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionA horizontal oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO' passing thorugh the end A figure. The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. find the velocity of the fluid relative to the tube as a function of the column height h.

View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
AincreaseBdecreaseCbecomes zeroDremain unchanged
A horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionFind the mass of a mole of colloid particles if during their centrifuging with an angular velocity ω about a vertical axis the concentration of the particles at the distance r2 from the rotation axis is η times greater than that at the distance r1 (in the same horizontal plane). The densities of the particles and the solvent are equal to ρ and to ρ0 respectively.
View SolutionA horizontally orientd tube of length l rotates with a constant angular velocity ω about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid.
The end A of tube is having pressure P0. The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0

View SolutionA horizontally oriented bent thin tube ABC of length 1.4m rotates with a constant angular velocity ω about a stationary vertical axis OO' passing through the end A as shown in figure. The portion BC of tube is parallel to OO' and its length is equal 0.4m. At t=0, AB part of tube is filled with an ideal fluid. The end A of tube is open, the closed end C has a very small orifice. Find the maximum height reached by fluid relative to end C. (take g=10/s2 and ω=10rad/s)

View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
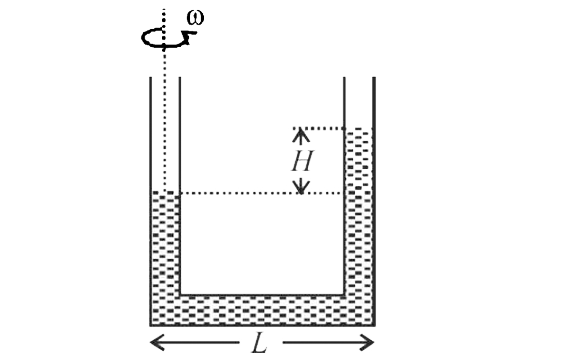
View Solution

