An impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
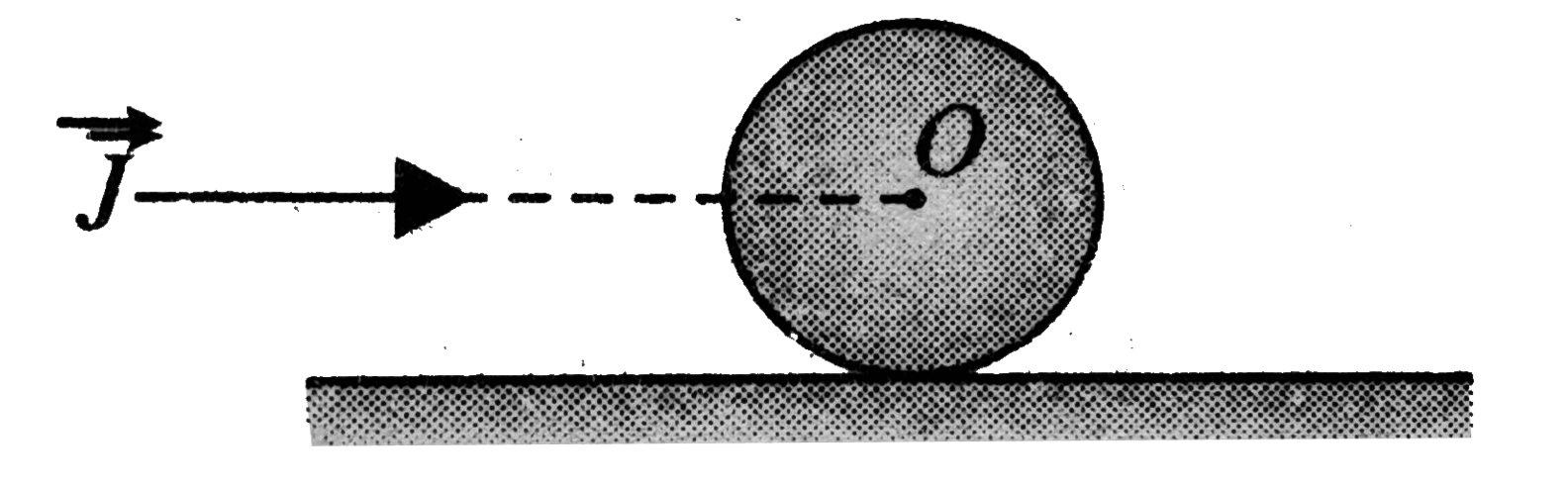
J/m
J/2m
J/4m
J/3m
The correct Answer is:B
Let v be the velocit of COM of ring just after the impule is applied and v' its velocity when pure rolling starts. Angular velocity ω of the ring at this instant will be ω=v′r.
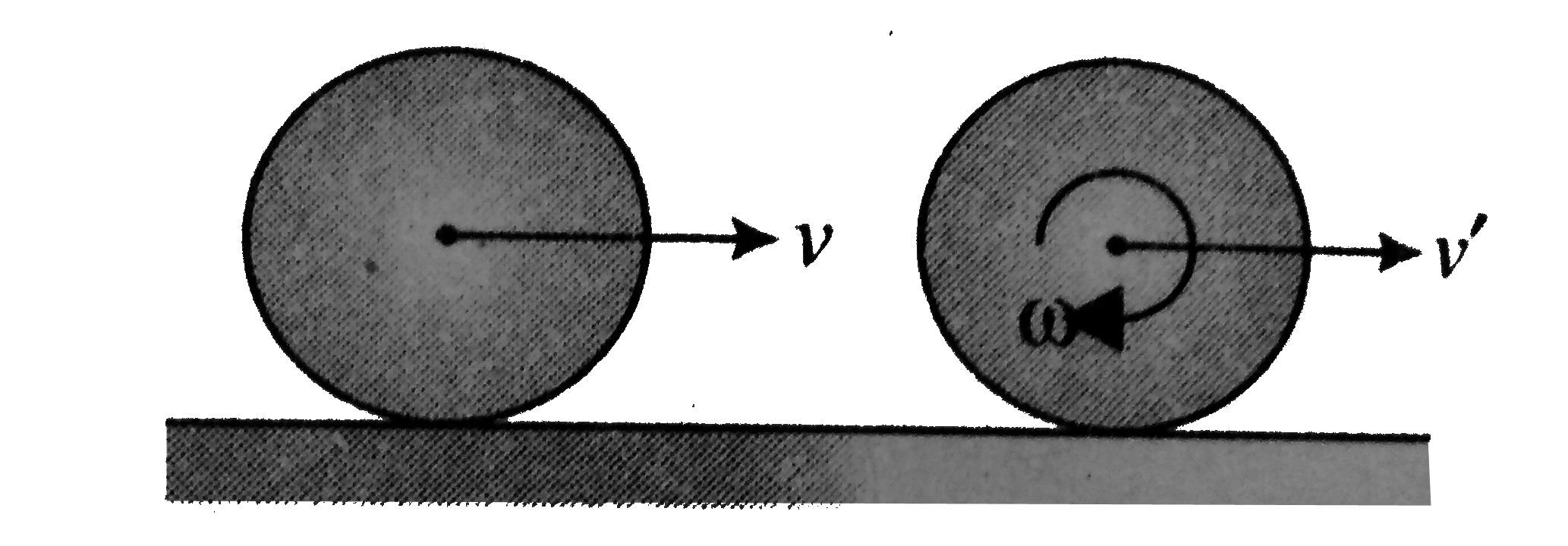
From impulse =change in linear momentum, we have
J=mv
or v=Jm.....i
Between the two positions shown in figure, force of friction on the ring acts backwards. So angular momentum of the ring about bottommost point will remain conserved
∴Li=Lf
or mr=mv'r+Iω
mv'r+(mr2)(v′r)=2mg'r
v'=v2=J2m (from equation)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Calculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
Radius of gyration of a ring about a transverse axis passing through its centre is
A0.5× diameter of ringBdiameter of ringC2× diameter of ringD(diameter of ring)2A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
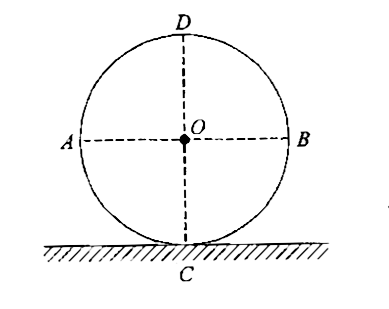 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20A ring performs pure rolling on a horizontal fixed surface with its centre moving with speed v.
AMaximum possible speed that any particle of ring may have is v/√2BMinimum possible speed that any particle of ring may have is v/√2Cparticles on the ring may have speed anywhere between 0 and 2u.DNone of these
The moment of inerta of a ring of mass 1kg about an axis passing through its centre perpendicular to its surface is 4kgm2. Calculate the radius of the ring.
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionThe escape velocity form the centre of a unifrom ring of mass M and radius R is :
View Solution
